Сила давления на вертикальную стенку. Сила давления жидкости на криволинейные поверхности
Силу гидростатического давления на криволинейную поверхность определяют по формуле
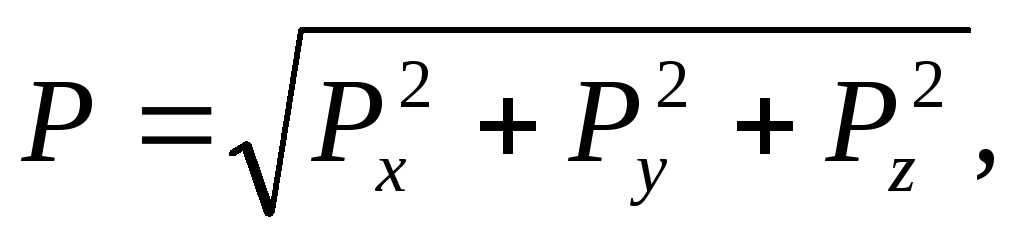
где
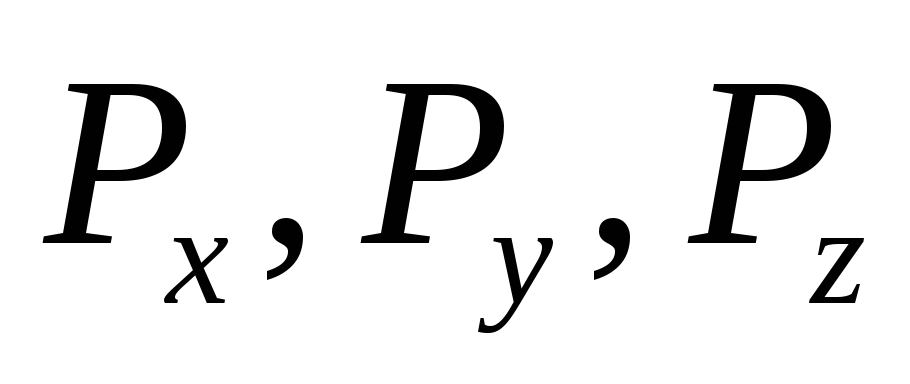 -
составляющие силы избыточного давления
по соответствующим координатным осям.
В случае цилиндрической криволинейной
поверхности
-
составляющие силы избыточного давления
по соответствующим координатным осям.
В случае цилиндрической криволинейной
поверхности
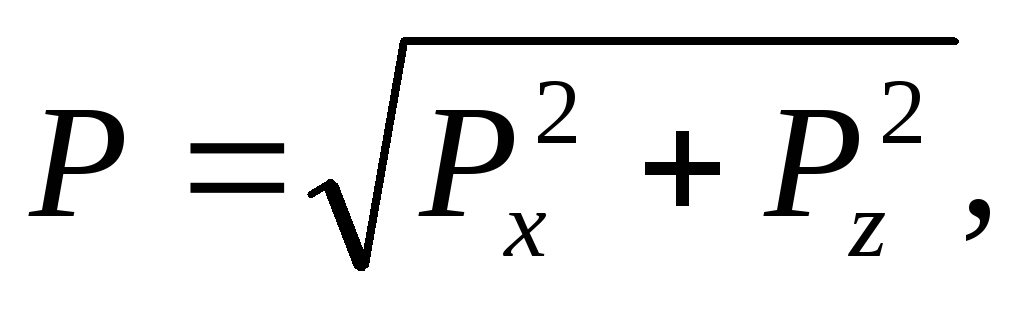
где
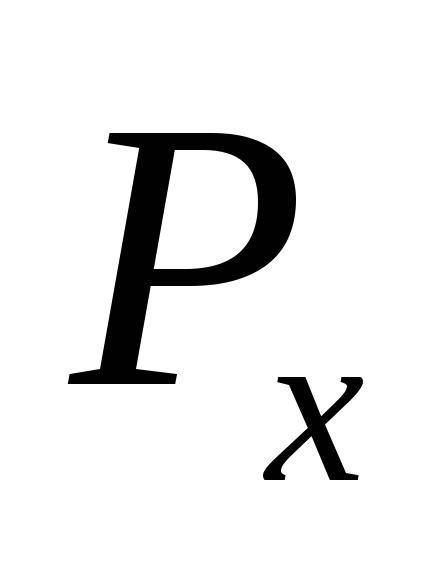 и
и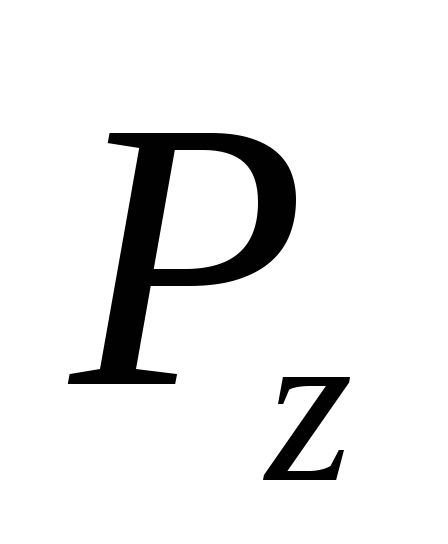 - горизонтальная и вертикальная
составляющие силыР.
- горизонтальная и вертикальная
составляющие силыР.
Горизонтальная составляющая избыточного давления Р х равна силе давления на вертикальную проекцию криволинейной поверхности
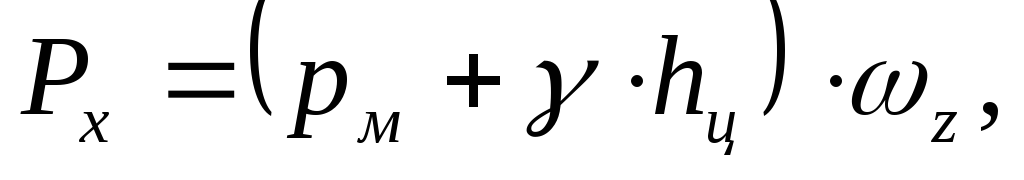
где р м - манометрическое давление на поверхности жидкости,
h ц - глубина погружения центра тяжести вертикальной проекции криволинейной поверхности;
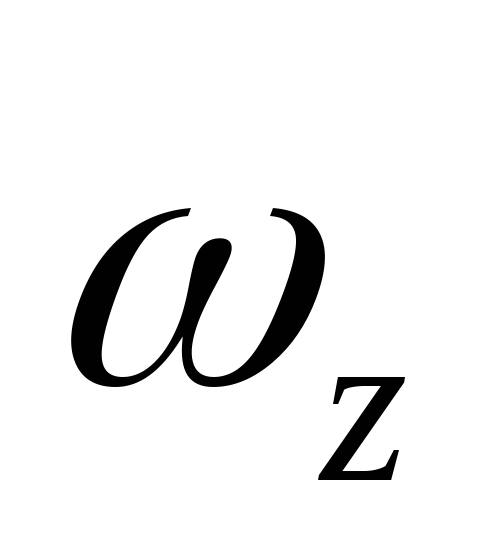 -
площадь вертикальной проекции
криволинейной поверхности. Если
манометрическое давление на свободной
поверхности жидкости равно нулю
(р o = р а), то
-
площадь вертикальной проекции
криволинейной поверхности. Если
манометрическое давление на свободной
поверхности жидкости равно нулю
(р o = р а), то

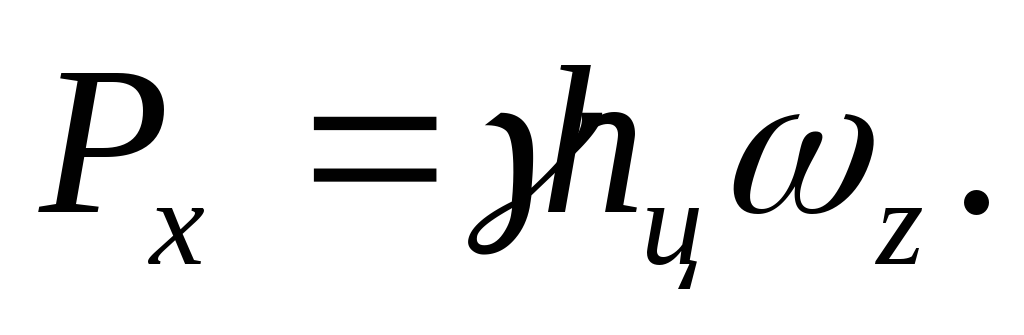
В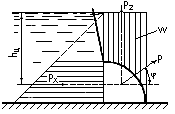 ертикальная
составляющая
ертикальная
составляющая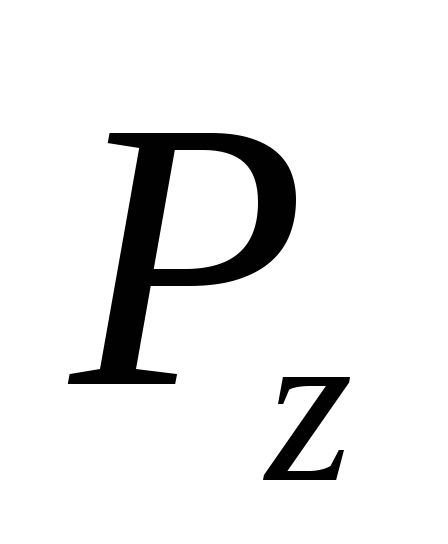 равна весу жидкости в объеме тела
давления. Тело давления расположено
между вертикальными плоскостями,
проходящими через крайние образующие
цилиндрической поверхности, самой
цилиндрической поверхностью и свободной
поверхностью жидкости или ее
продолжением.
равна весу жидкости в объеме тела
давления. Тело давления расположено
между вертикальными плоскостями,
проходящими через крайние образующие
цилиндрической поверхности, самой
цилиндрической поверхностью и свободной
поверхностью жидкости или ее
продолжением.
Если давление на свободной поверхности
жидкости
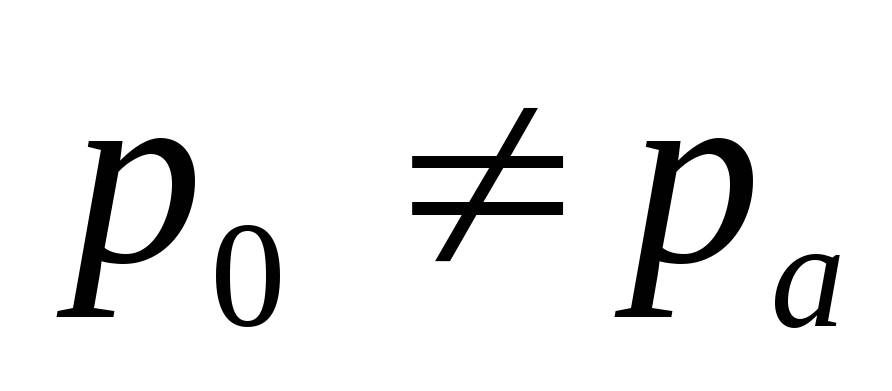 ,
то тело давления ограничивается сверху
пьезометрической плоскостью, удаленной
от свободной поверхности жидкости на
расстояние
,
то тело давления ограничивается сверху
пьезометрической плоскостью, удаленной
от свободной поверхности жидкости на
расстояние
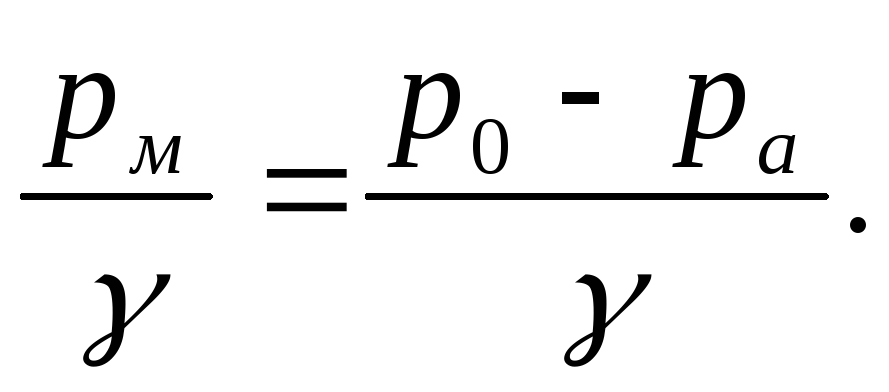
Направление силы Р
определяется
тангенсом угла :
:
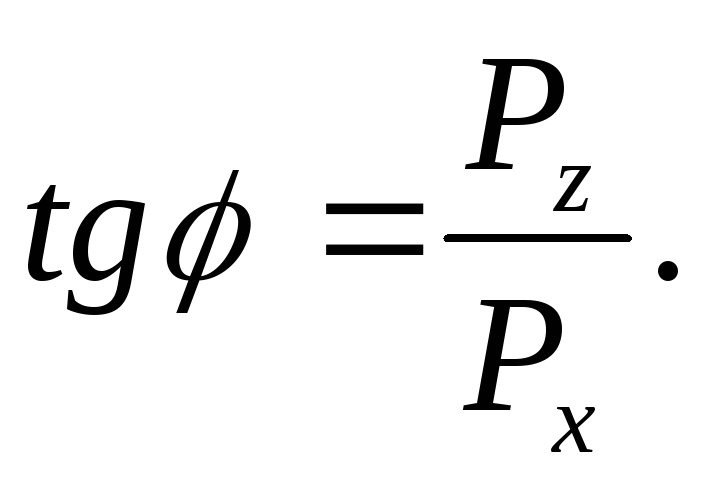
Если криволинейная поверхность не цилиндрическая, то горизонтальную составляющую Р y определяют аналогично силеР х .
Примеры
2.28.
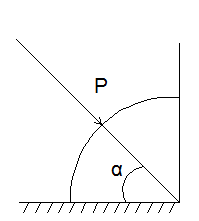
Определить силу давления воды
на деталь, имеющую форму четверти
кругового цилиндра радиуса =0,5 м. Найти
угол ,
под котором эта сила направлена к
горизонту. Расчет вести на единицу
ширины конструкции. Высота конструкции
Н=5 м.
,
под котором эта сила направлена к
горизонту. Расчет вести на единицу
ширины конструкции. Высота конструкции
Н=5 м.
Р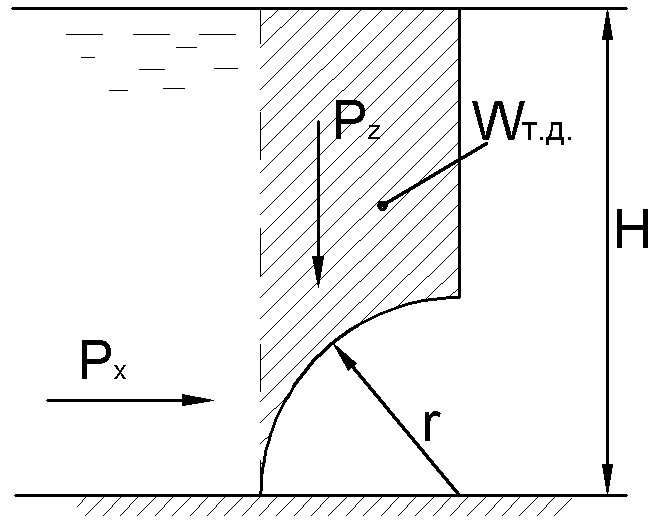 ешение:
ешение:
Найдем горизонтальную составляющую силы гидростатического давления воды:
Р x =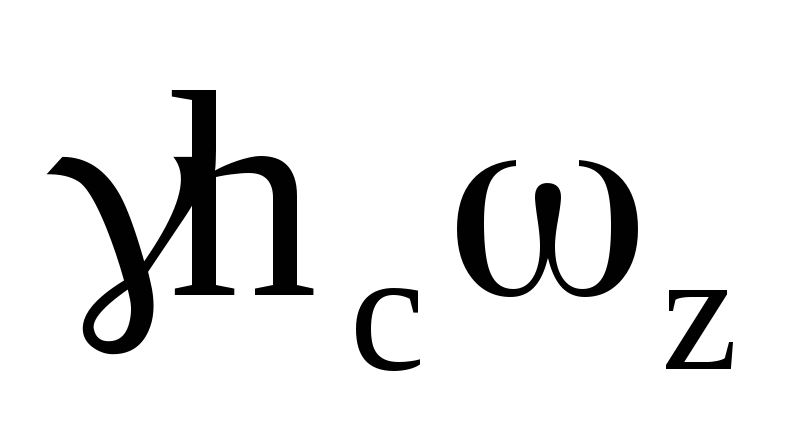 ,
,
где h c =H-;
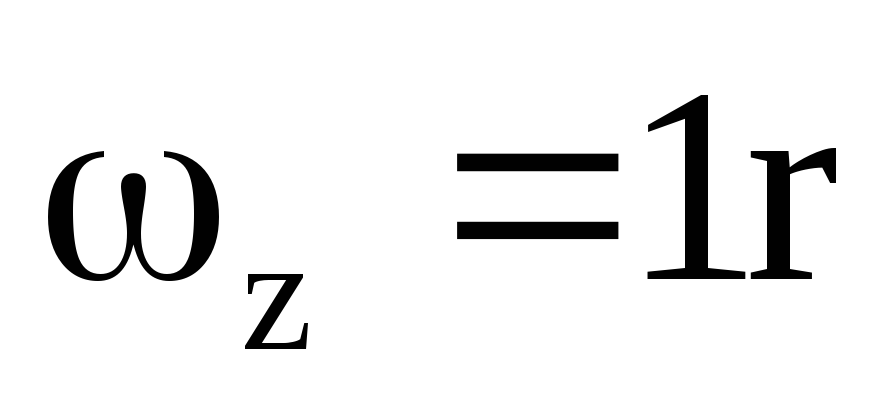 ;
;
=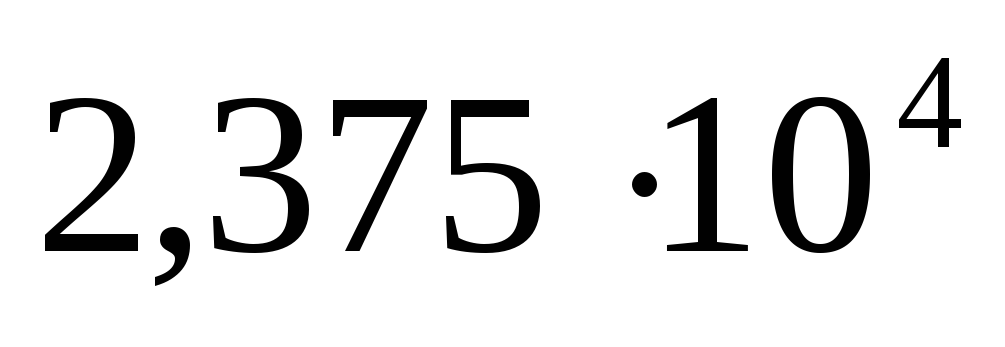 Н.
Н.
Найдем вертикальную составляющую:
P z =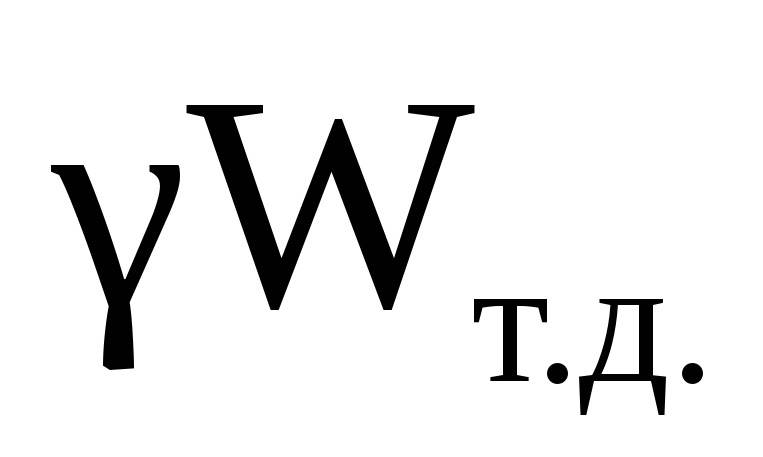 .
.
Для чего определим объем тела давления:
Тогда
Pz
= 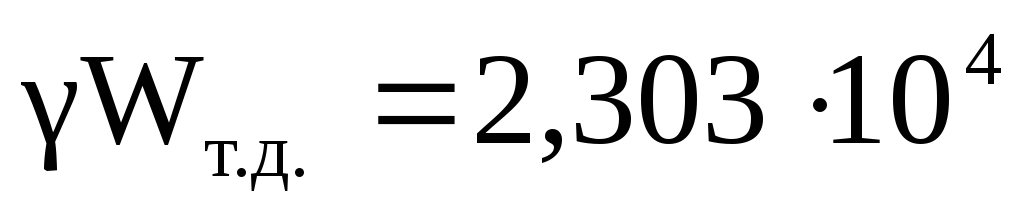 H .
H .
Результирующая сила найденных составляющих равна:
Р
= 3,31 Н.
Н.
Угол между линией действия этой силы и линией горизонта равен:
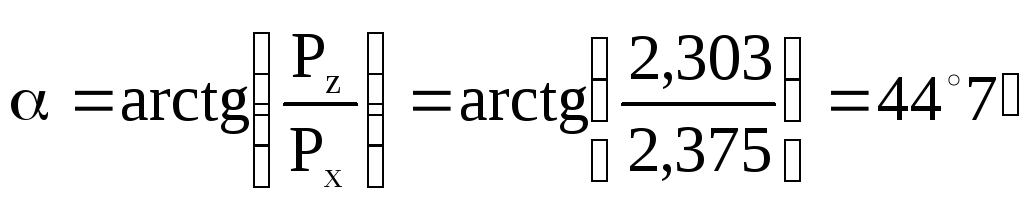
Ответ
:P= 3, 31  H;
H;
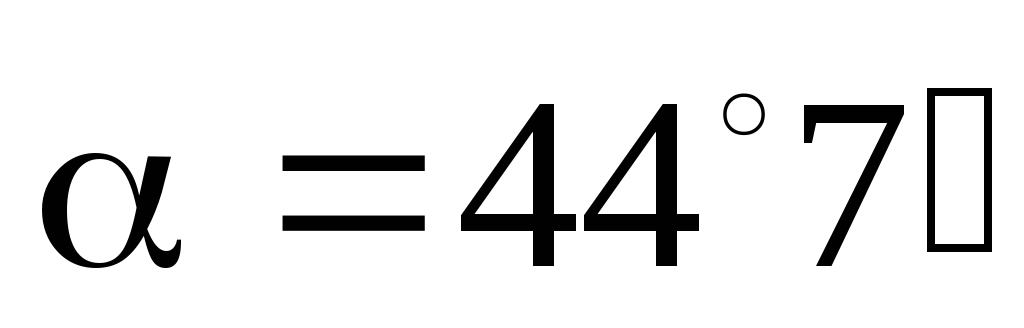 .
.
2.29 . Определить величину Р и направление угол α равнодействующей силы давления на цилиндрический затвор плотины, перекрывающий прямоугольное отверстиеh=D= 1,0 м и ширинойb= 5,0 м. Глубина воды слева -H 1 = 3,4 м, справа -H 2 =D/2.
Решение: 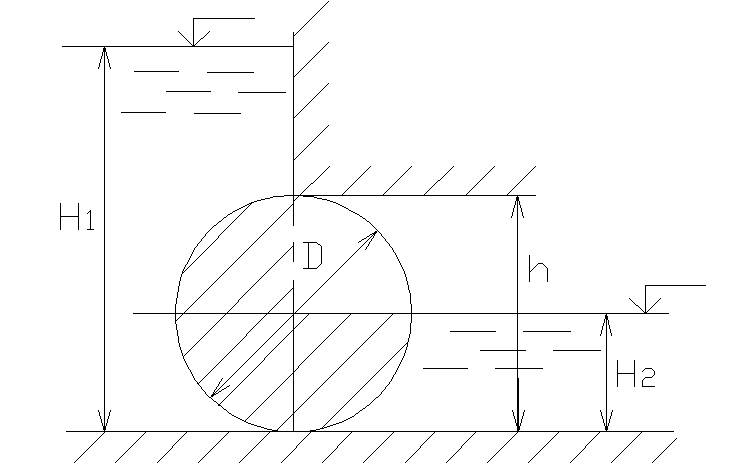 Для
нахождения силы гидростатического
давления на цилиндр необходимо
использовать зависимость:
Для
нахождения силы гидростатического
давления на цилиндр необходимо
использовать зависимость:
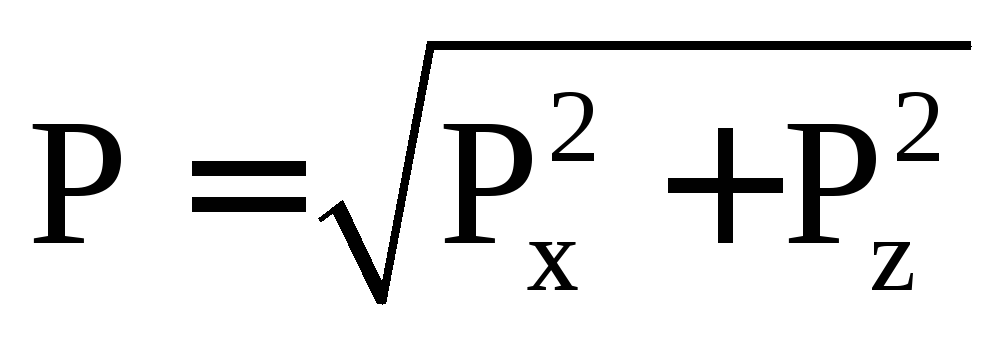 ,
,
где
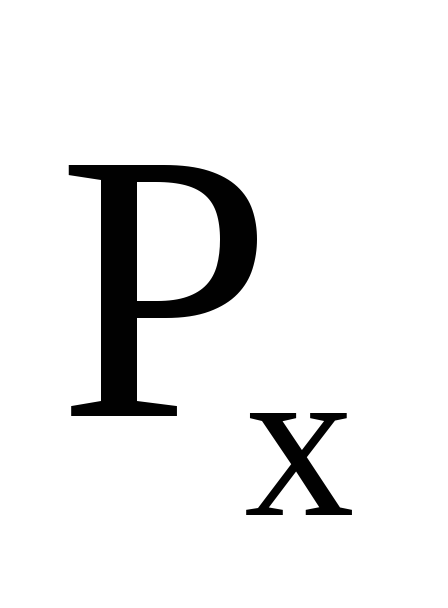 – горизонтальная
составляющая
полной силы гидростатического
давления воды;
– горизонтальная
составляющая
полной силы гидростатического
давления воды;
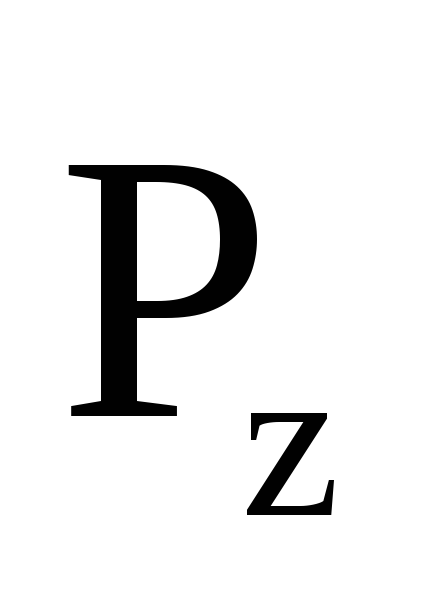 – вертикальная
составляющая полной силы
гидростатического давления воды.
– вертикальная
составляющая полной силы
гидростатического давления воды.
Направление равнодействующей силы гидростатического давления воды найдем по формуле:
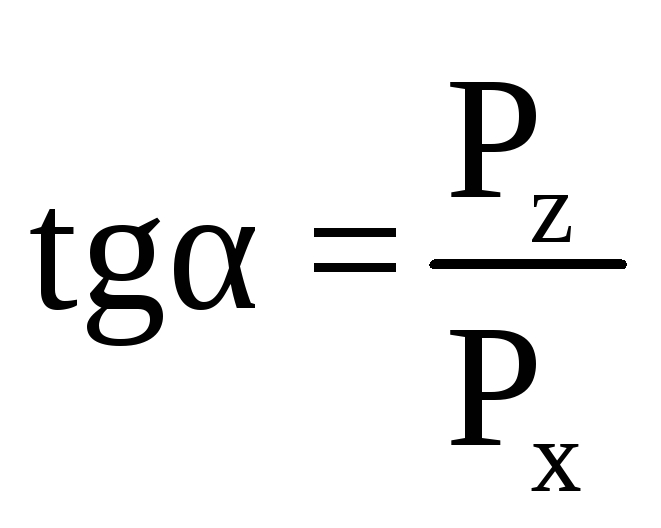
Горизонтальная составляющая силы давления воды:
Их равнодействующая величина равна алгебраической сумме:
Вертикальная составляющая силы давления на затвор равна весу воды в объеме тела давления (на рисунке заштриховано):
Результирующая сила гидростатического давления на цилиндрический затвор составит:
Направление этой силы, т.е. угол наклона к горизонту составит:
![]() .
.
Ответ:
2.30.
Определить силу суммарного
давления на торцовую плоскую стенку
цилиндрической цистерны диаметром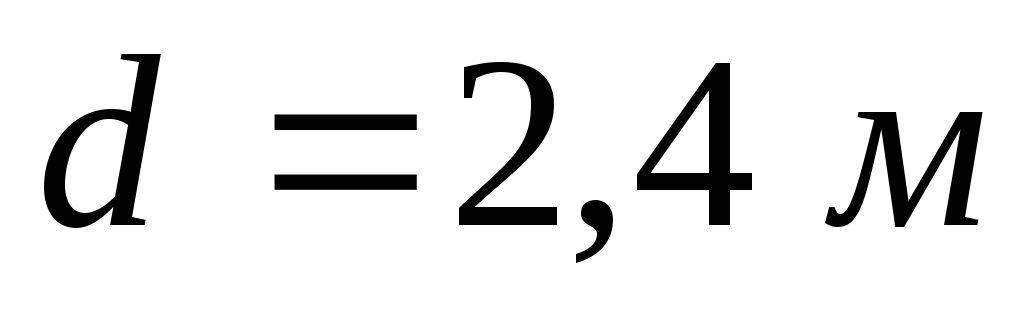 и точку её приложения. Высота горловины
и точку её приложения. Высота горловины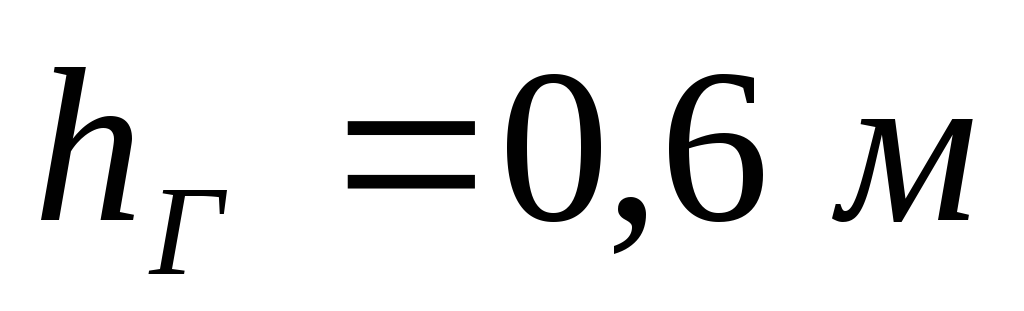 .
Цистерна заполнена бензином до верха
горловины.
.
Цистерна заполнена бензином до верха
горловины.
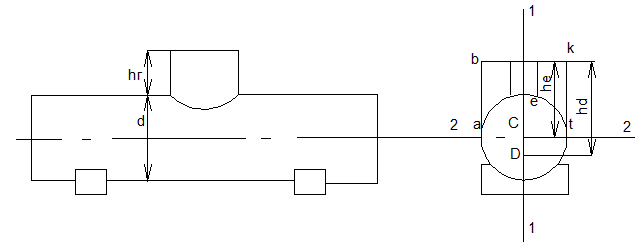
Решение . Сила суммарного давления бензина на торцовую стенку цистерны равна
где
 -
плотность бензина (табл. П-3).
-
плотность бензина (табл. П-3).
Точка приложения (центр давления) силы суммарного давления расположена на глубине (от верхней кромки горловины)
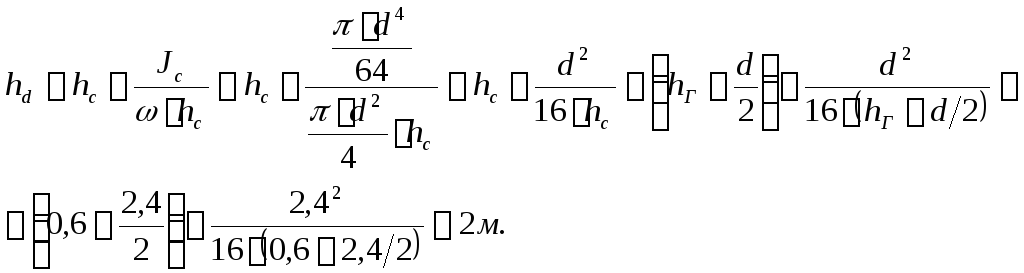
Ответ:
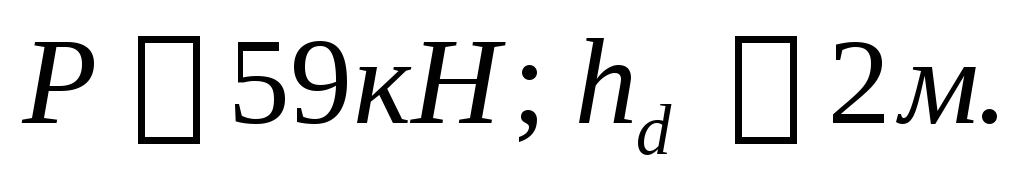
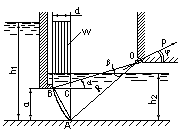
2.31.
Определить силу суммарного
давления на секторный затвор и её
направление. Глубина воды перед затвором
Н=4м, длина затвораL=8м,
угол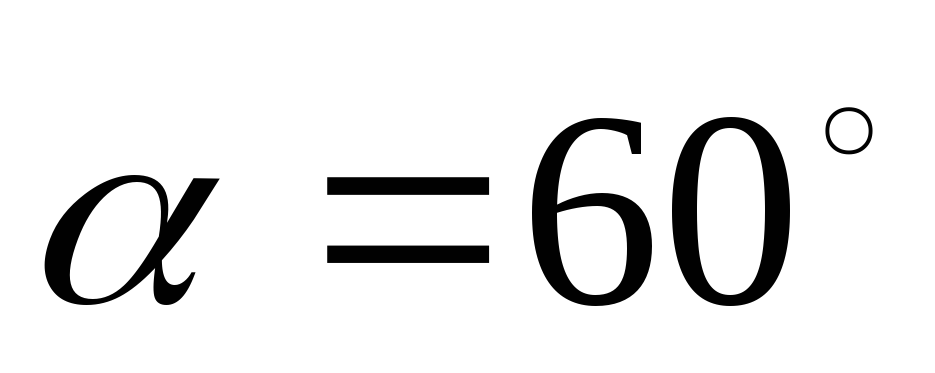 .
.
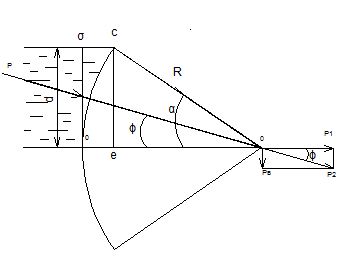
Решение. Горизонтальная составляющая полной силы давления на секторный затвор равна силе давления на вертикальную проекцию затвора:
Вертикальную составляющую полной силы давления на секторный затвор определяем по формуле:
где W- объём тела давленияabcдлинойL;
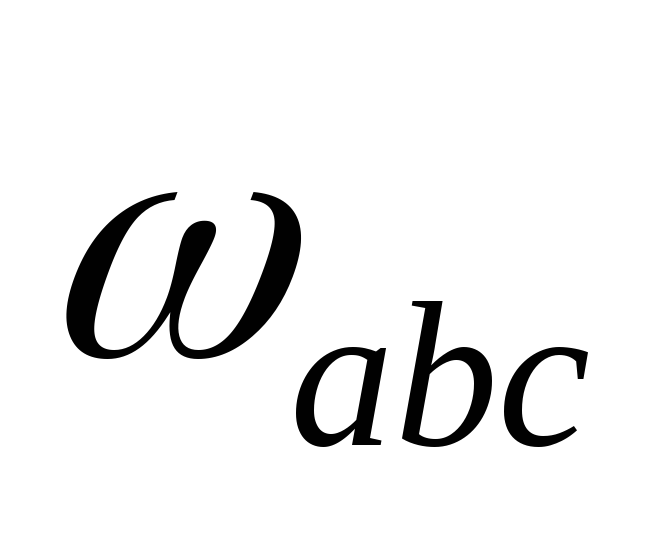 -
площадь фигурыabc;
-
площадь фигурыabc;
Найдем элементы
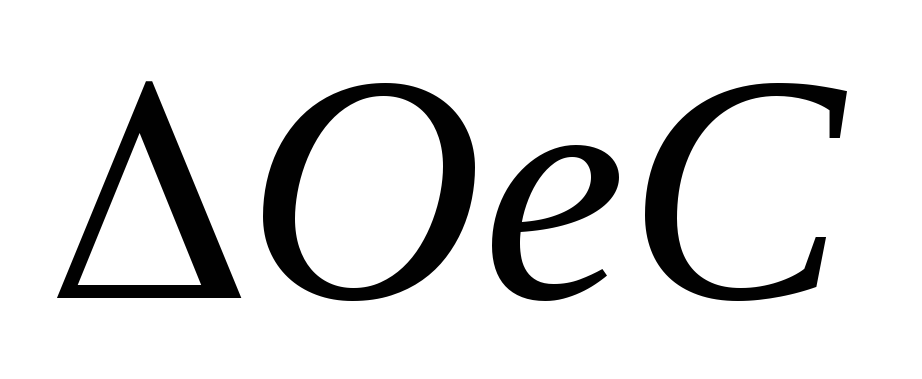 и площадь фигурыabc:
и площадь фигурыabc:
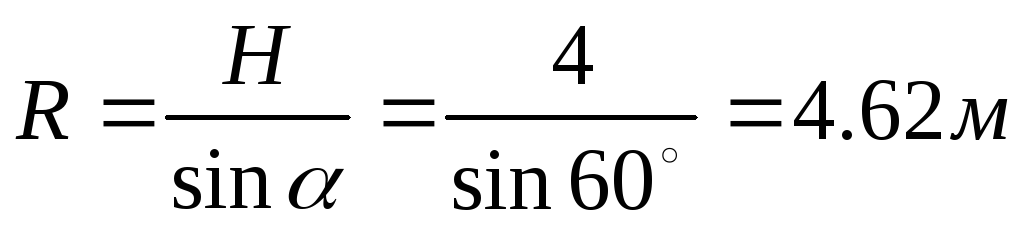 ;
;
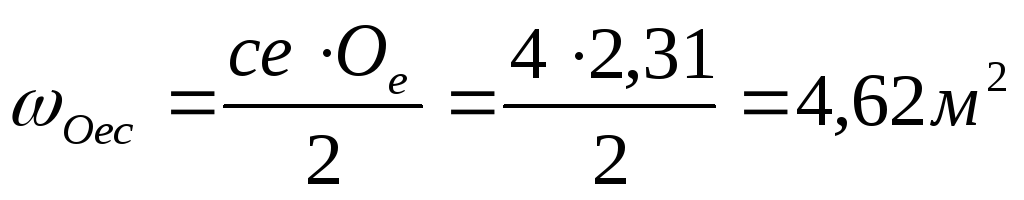 ;
;
Равнодействующую сил давлений определяем по формуле:
Направление этой силы определяется
углом
 :
:
;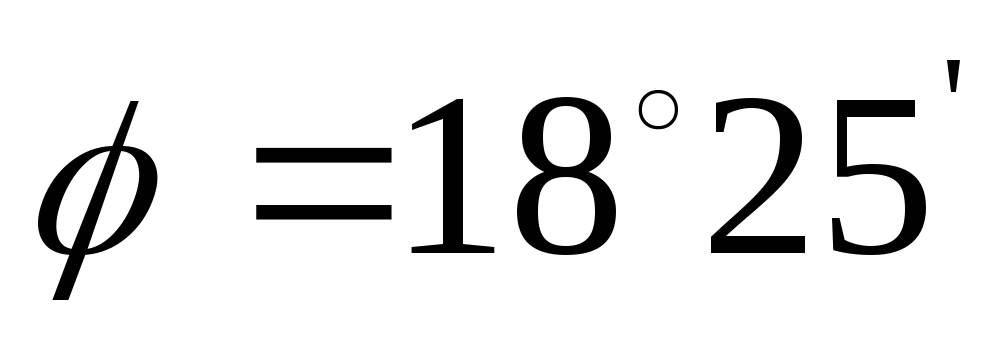 .
.
Ответ:
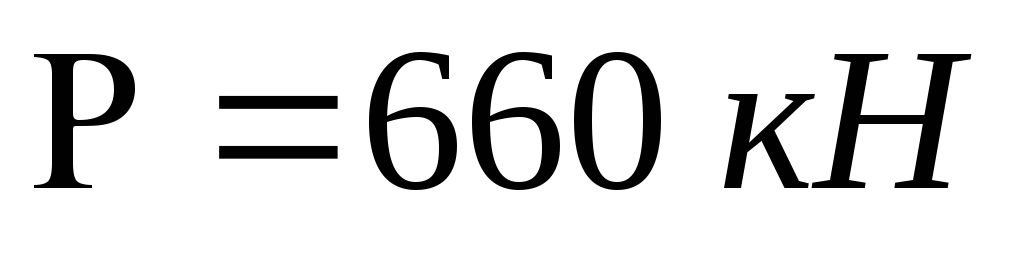 ;
;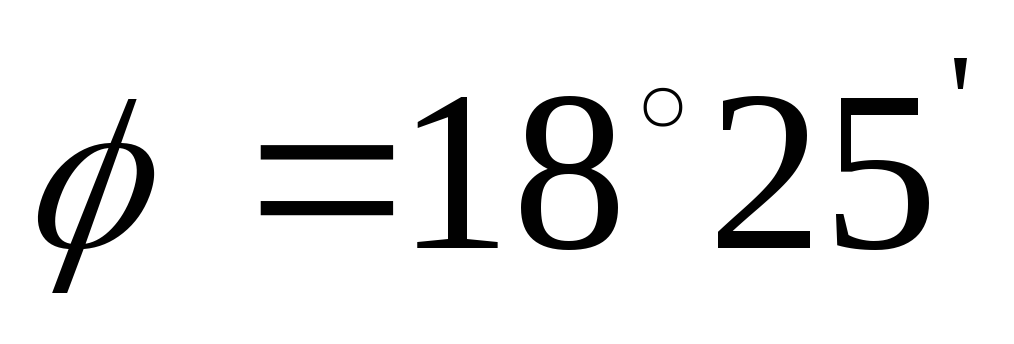 .
.
2.32.
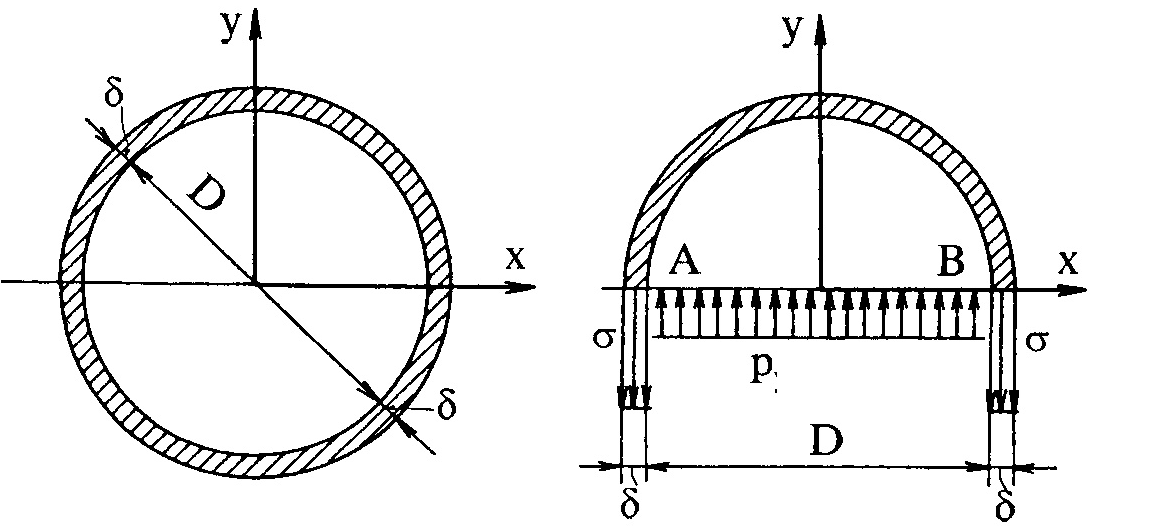
По стальному трубопроводу
диаметром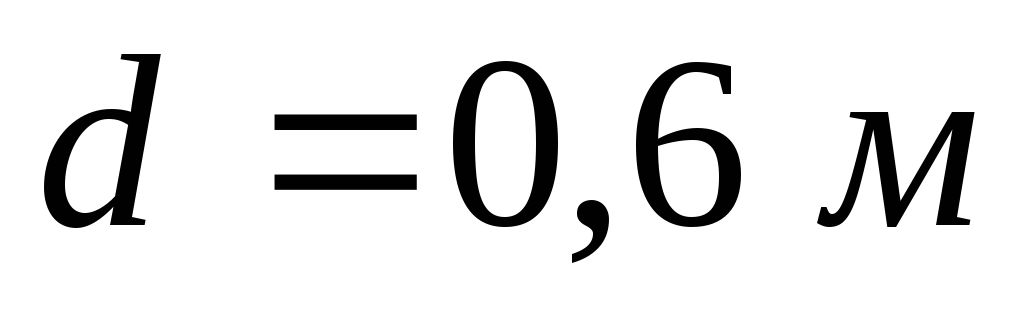 подаётся вода под давлением
подаётся вода под давлением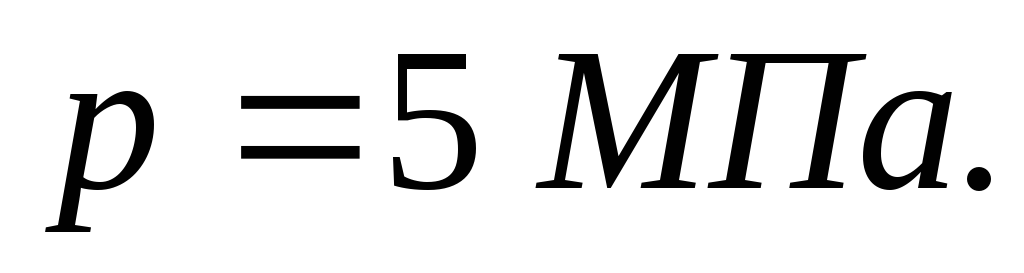 Определить напряжение в стенке трубы,
если ее толщина
Определить напряжение в стенке трубы,
если ее толщина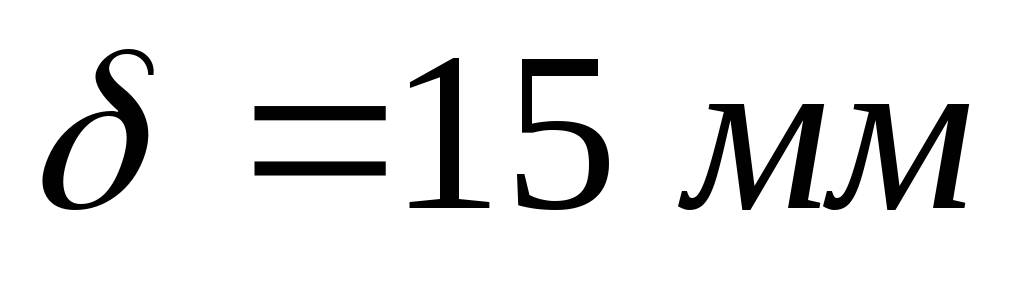 .
.
Решение. Суммарная сила давления, разрывающая трубу в продольном направлении, равна гидростатическому давлению, умноженному на площадь вертикальной проекции криволинейной стенки:
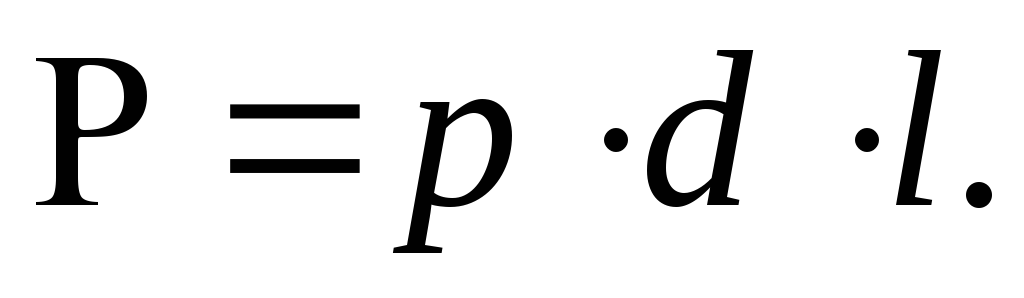
Разрыв происходит по двум продольным сечениям стенки трубы. Напряжение, возникающее в материале стенки, равно

Ответ:
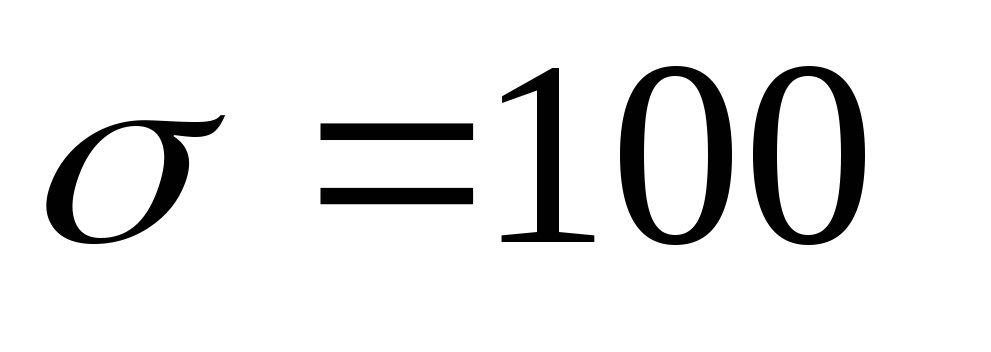 МПа
МПа
2.33.
Определить силы, разрывающие
горизонтальную, наполненную бензином
цистерну длиной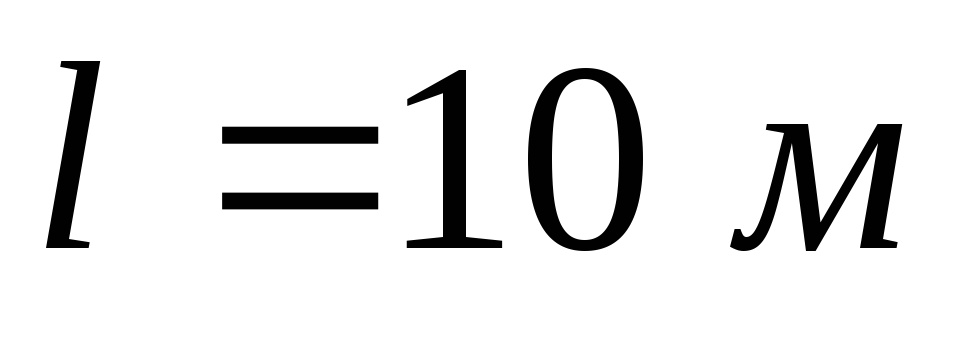 по сечениям
по сечениям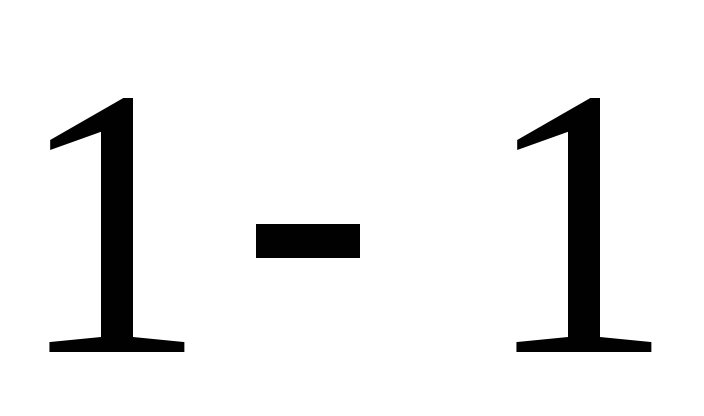 и
и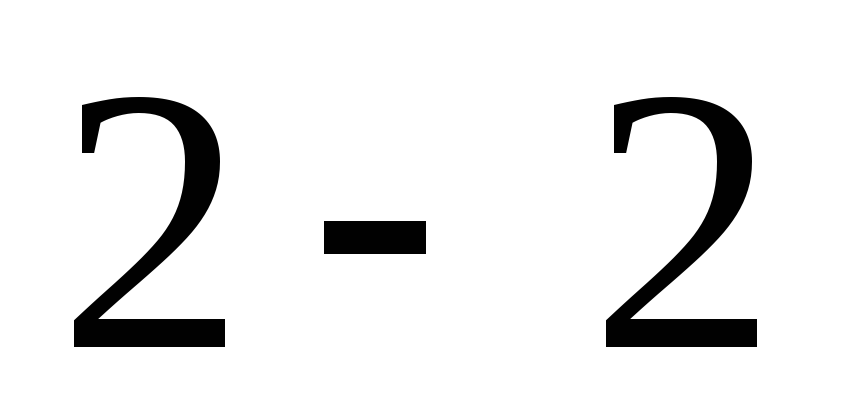 ,
если диаметр цистерны
,
если диаметр цистерны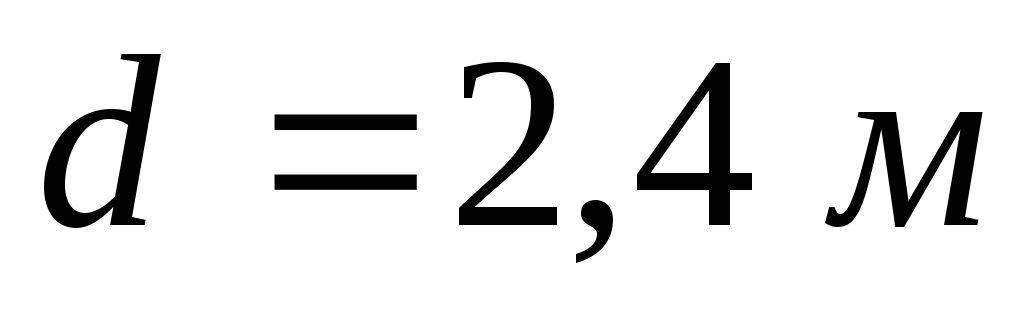 ,
а высота горловины
,
а высота горловины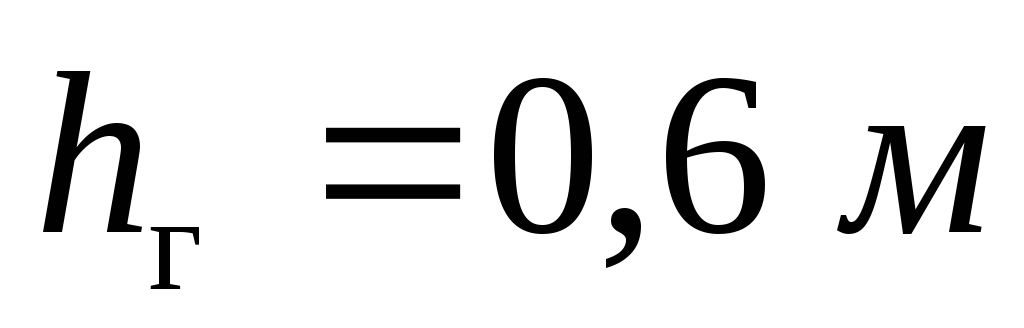 .
Цистерна заполнена бензином плотностью
.
Цистерна заполнена бензином плотностью =740кг/
=740кг/
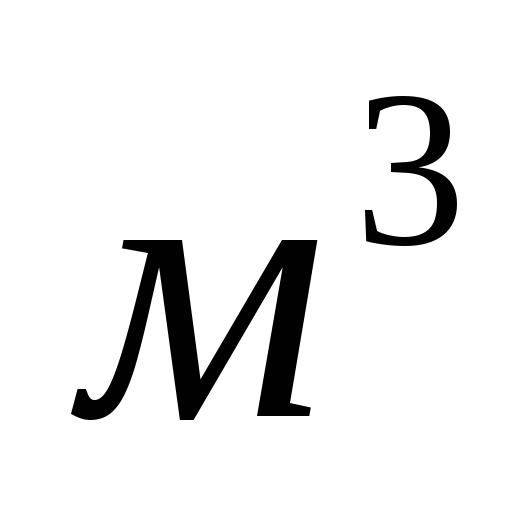 до верха горловины.
до верха горловины.

Решение.
Сила, разрывающая цистерну
по сечению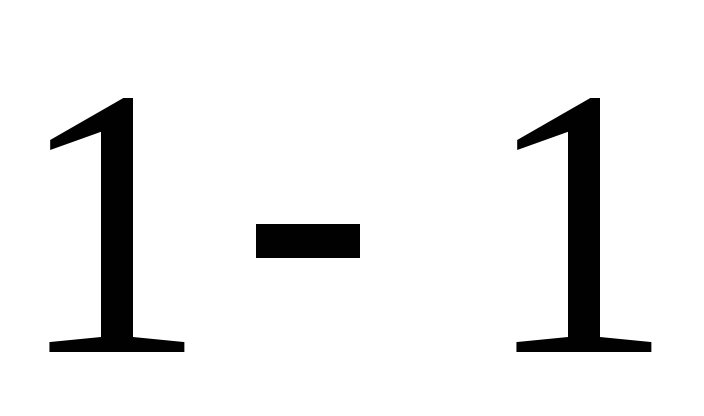 ,
равна горизонтальной составляющей силы
давления воды на криволинейную стенку
,
равна горизонтальной составляющей силы
давления воды на криволинейную стенку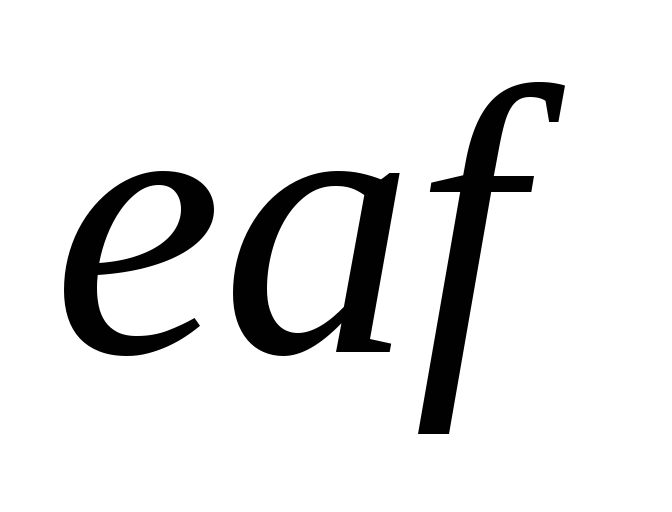 или
или :
:
Силы, растягивающие цистерну по сечению 2-2, равны силам, действующим на криволинейные стенки aetиaft. Эти силы также направлены противоположно друг другу. Сила давления на криволинейную стенкуaet
 ,
,
где W– объём телаabkt;
ω – площадь фигуры abktea;
Подставляя цифровые значения, находим:
Ответ:
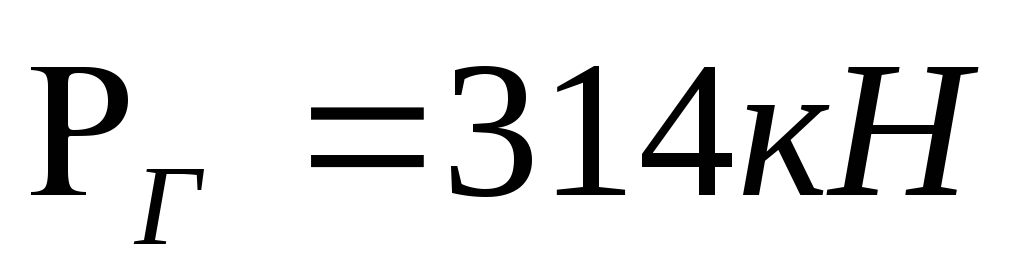 ;
; .
.
2.34.
Для выпуска сточных вод в море
построен трубопровод диаметром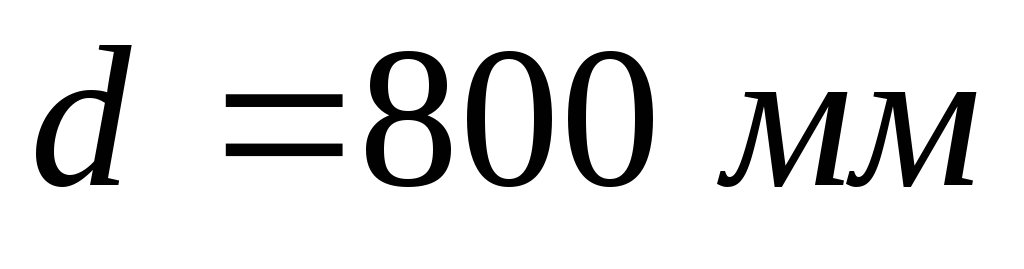 ,
уложенный по дну на глубине
,
уложенный по дну на глубине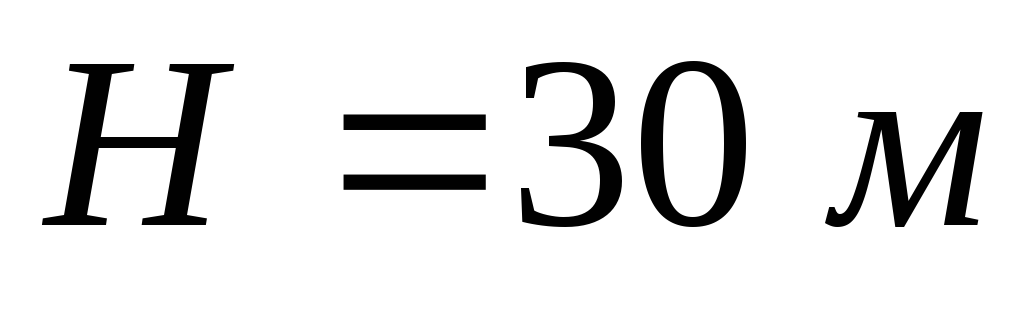 .
Определить силы, действующие на
трубопровод, когда он не заполнен.
.
Определить силы, действующие на
трубопровод, когда он не заполнен.
Решение.
Сила, действующая на
трубопровод сверху, определяется как
вертикальная составляющая суммарных
сил давления на криволинейную поверхность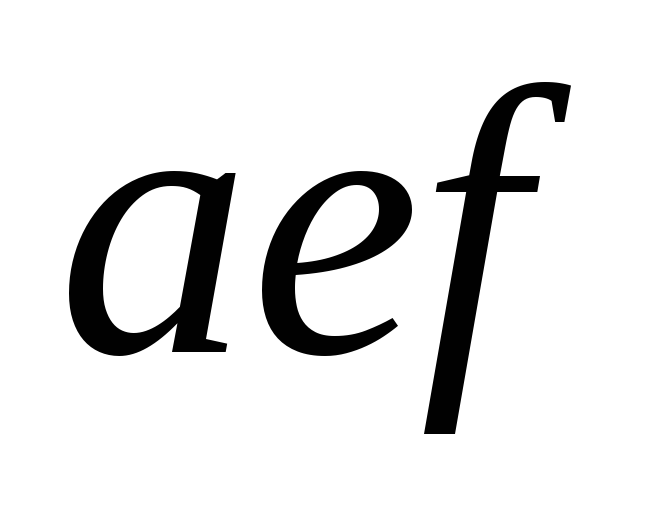 .
Она равна весу воды в объёме тела
.
Она равна весу воды в объёме тела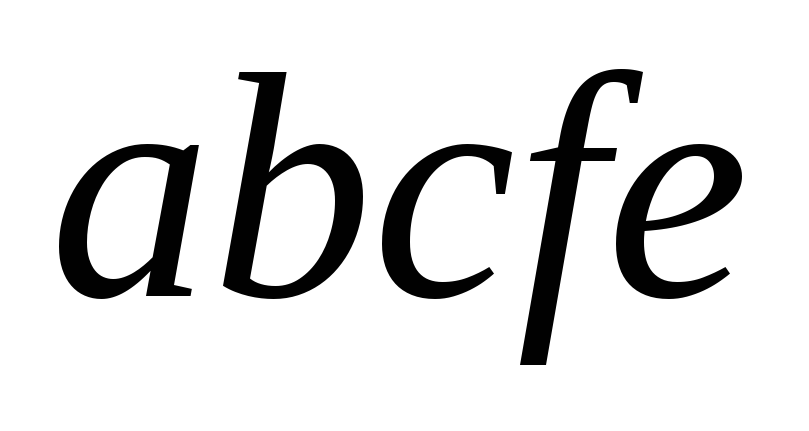 ,
т.е. (на
,
т.е. (на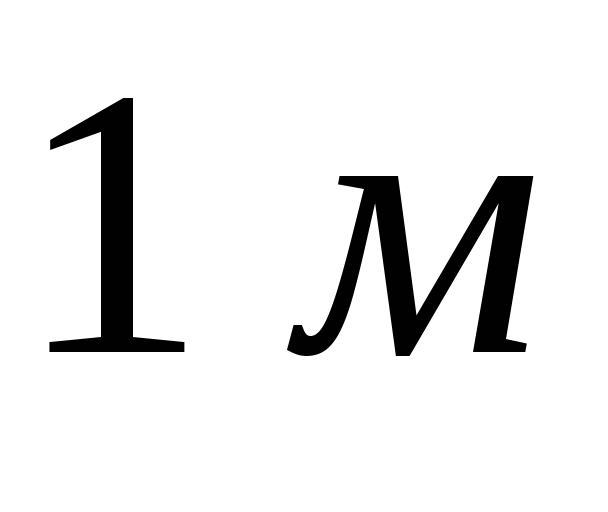 длины трубопровода)
длины трубопровода)
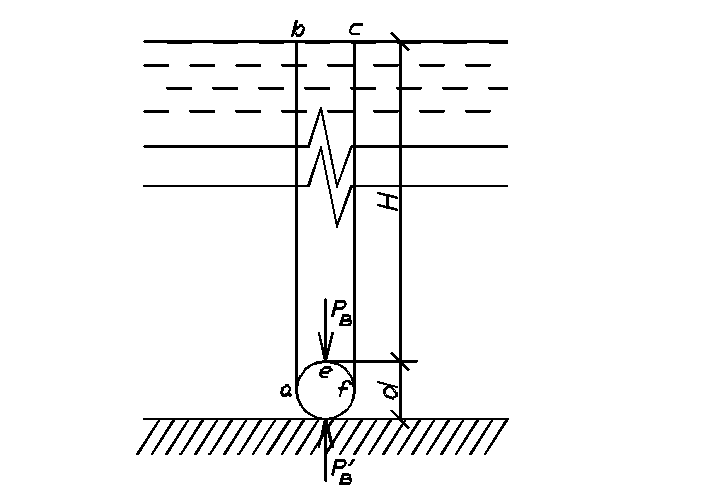
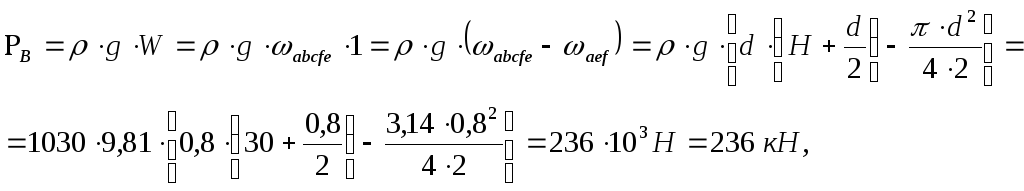
где
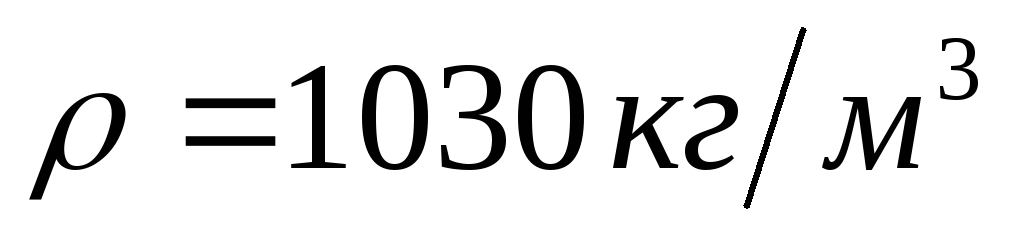 -
плотность морской воды (табл. П-3).
-
плотность морской воды (табл. П-3).
Сила
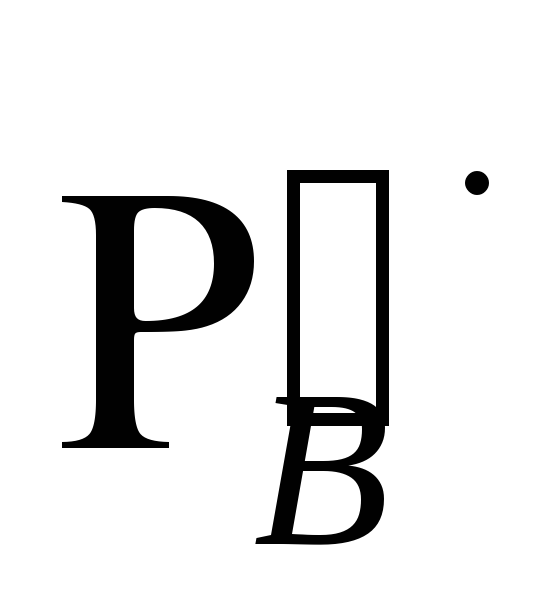 ,
действующая на трубопровод снизу, больше
силы
,
действующая на трубопровод снизу, больше
силы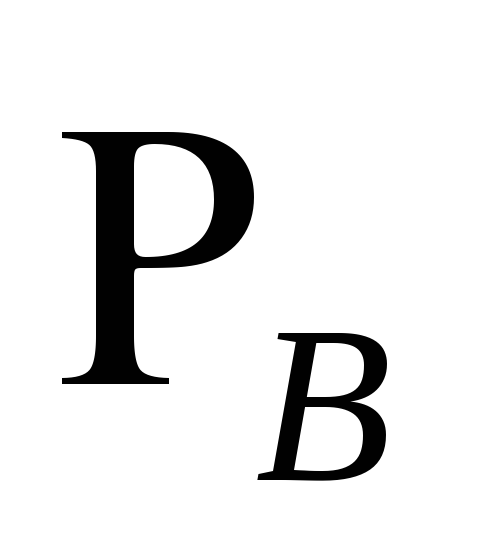 на величину веса воды в рассматриваемом
участке трубопровода, т.е.
на величину веса воды в рассматриваемом
участке трубопровода, т.е.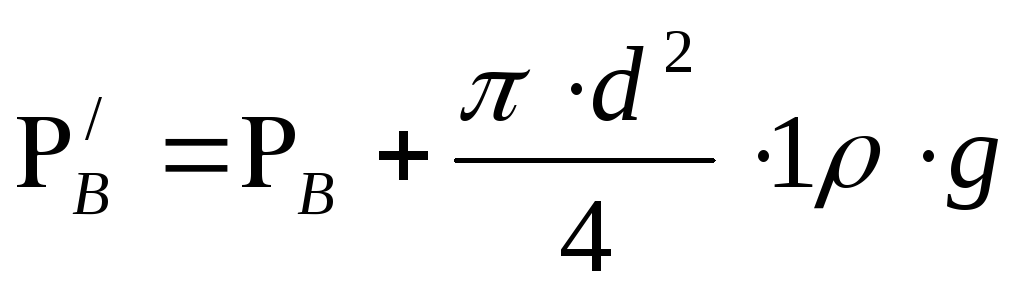 ;
собственный вес трубы
;
собственный вес трубы должен быть равен
должен быть равен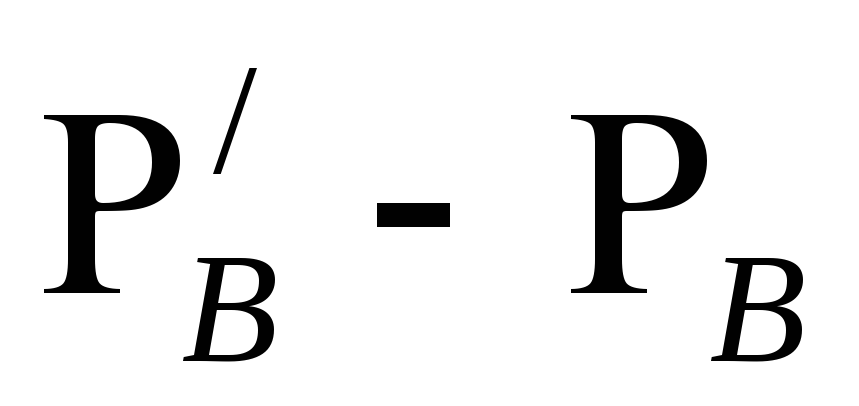 для того, чтобы исключить возможность
её всплывания.
для того, чтобы исключить возможность
её всплывания.
Силы, действующие на трубопровод по
горизонтали, равны и направлены
противоположно друг другу.Каждая из
этих сил равна горизонтальной составляющей
сил давления воды на криволинейную
стенку, которая, в свою очередь, равна
силе суммарного давления воды на
вертикальную проекцию трубы, т.е. (на
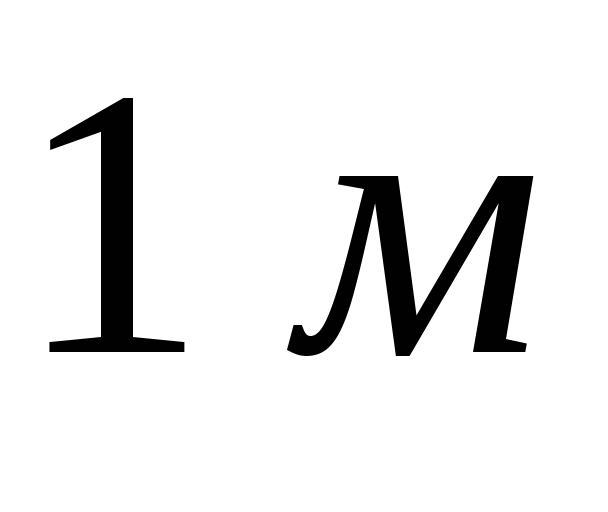 длины трубопровода)
длины трубопровода)
Ответ:
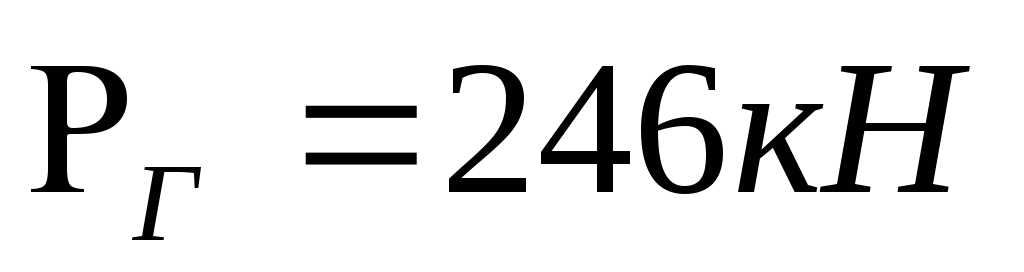 .
.
2.35.
Определить силу гидростатического
давления воды на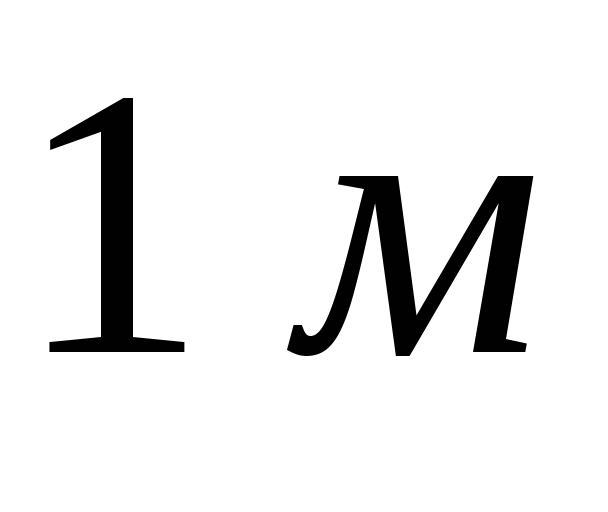 ширины нижней криволинейной части
сооружения, если
ширины нижней криволинейной части
сооружения, если
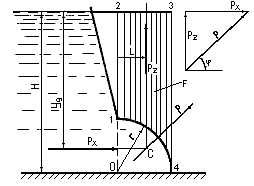
Решение.
1) Горизонтальная составляющая силы давления воды на криволинейную часть сооружения равна силе давления на вертикальную проекцию этой поверхности
2) Вертикальная составляющая
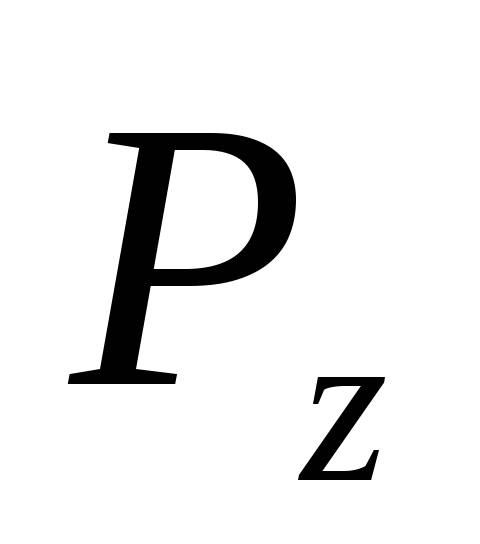 равна весу жидкости в объеме тела
давления. Обозначим площадь фигуры
равна весу жидкости в объеме тела
давления. Обозначим площадь фигуры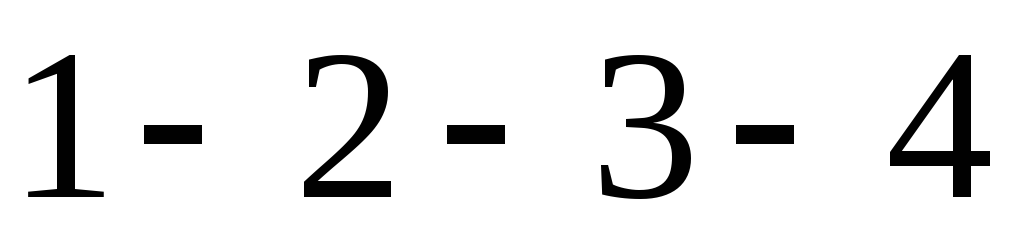 через
через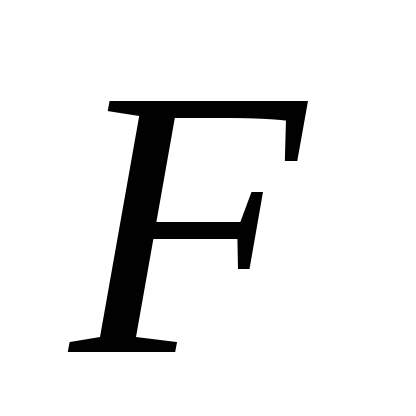 .
Тогда:
.
Тогда:
3) Суммарная сила давления воды на криволинейную часть сооружения
4) Расстояние от свободной поверхности воды до линии действия горизонтальной составляющей Р х .
5)
Вертикальная составляющая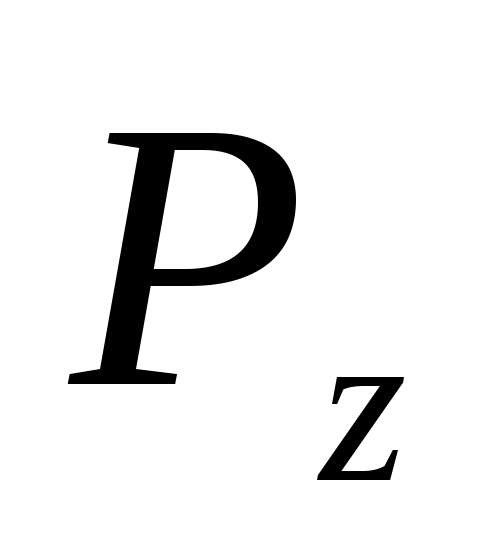 проходит через центр тяжести фигуры
проходит через центр тяжести фигуры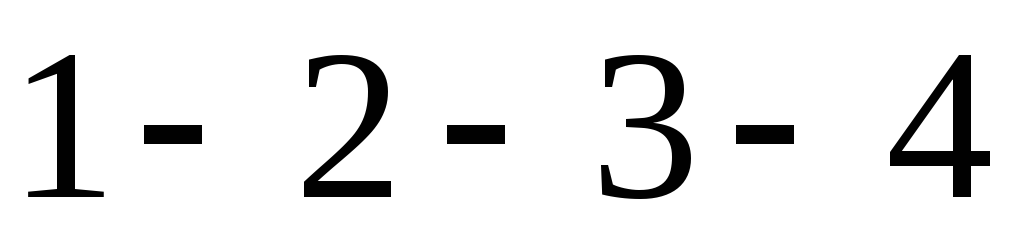 .
Расстояние
.
Расстояние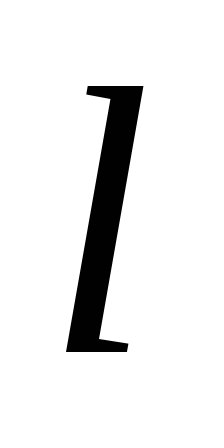 центра тяжести фигуры
центра тяжести фигуры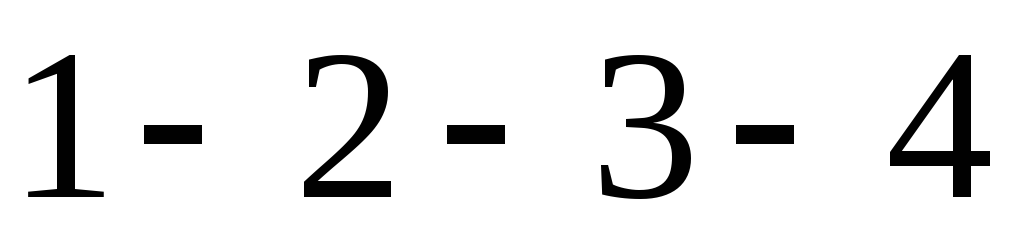 от линии
от линии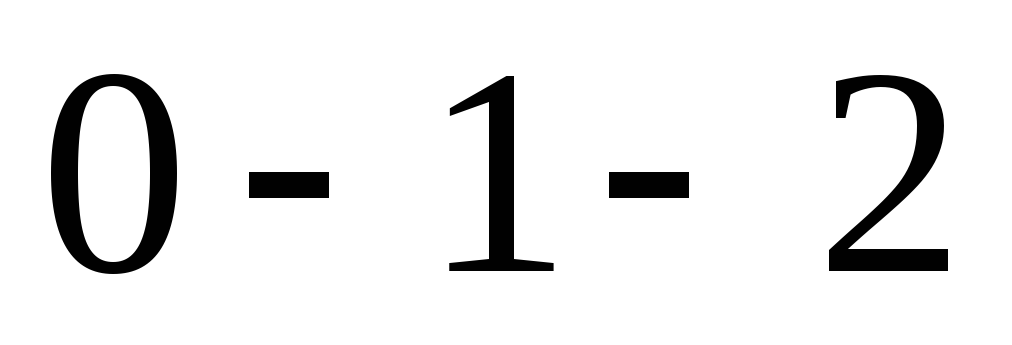 равно статическому моменту этой
фигуры
равно статическому моменту этой
фигуры относительно линии
относительно линии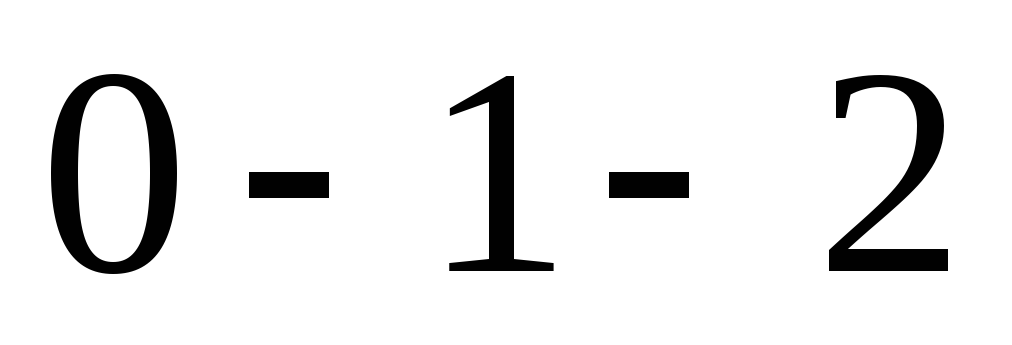 ,
деленному на площадь фигуры
,
деленному на площадь фигуры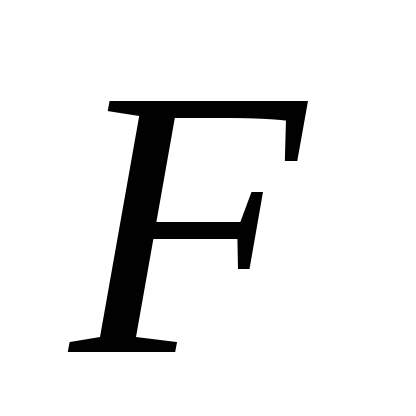 ,
причем расстояние центра тяжести
четверти круга
,
причем расстояние центра тяжести
четверти круга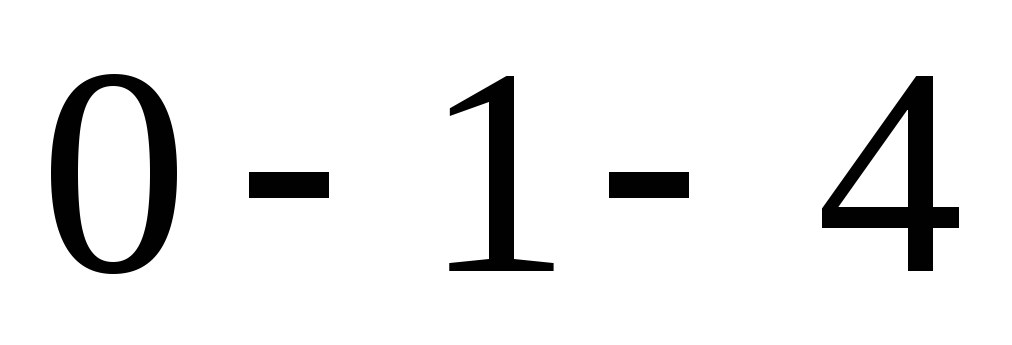 от линии
от линии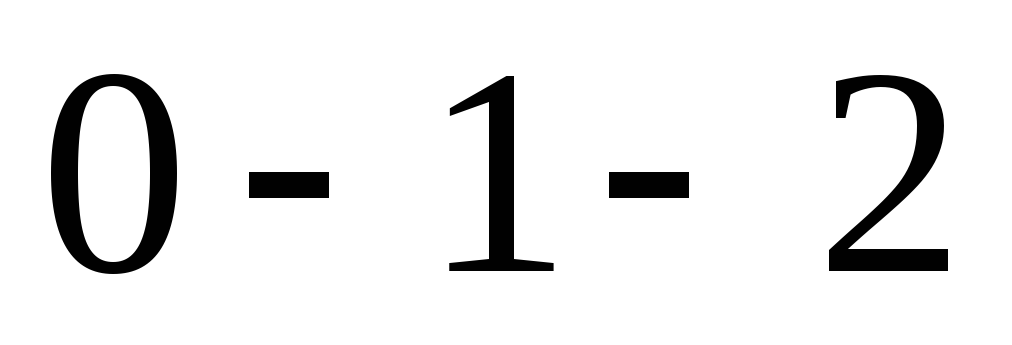 :
:
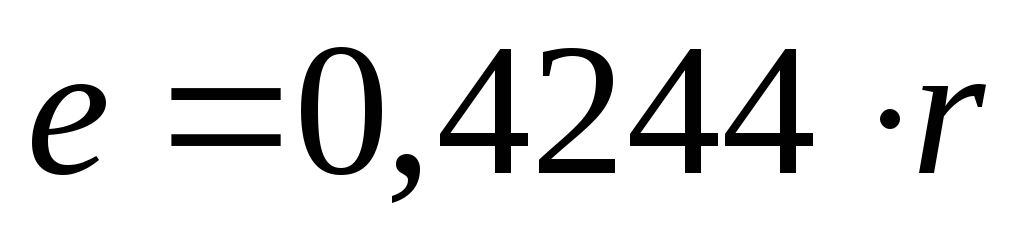 ;
;
Сила
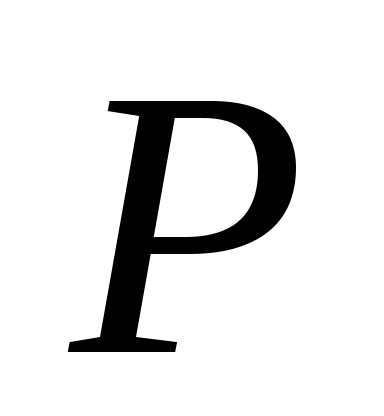 проходит через точку пересеченияc
линий действия горизонтальной и
вертикальной составляющих под углом
проходит через точку пересеченияc
линий действия горизонтальной и
вертикальной составляющих под углом к горизонту, причем
к горизонту, причем
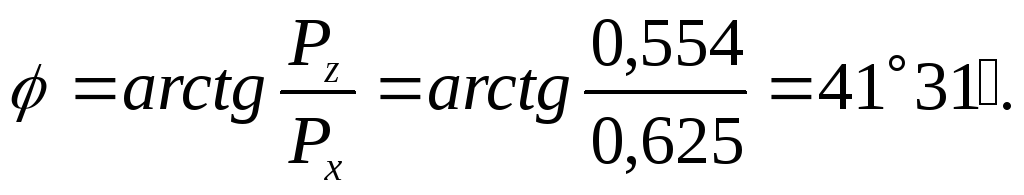
Заметим, что при круговой цилиндрической
поверхности сила
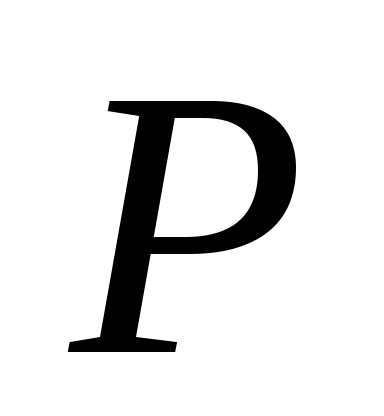 всегда проходит через центр круга.
всегда проходит через центр круга.
Ответ:
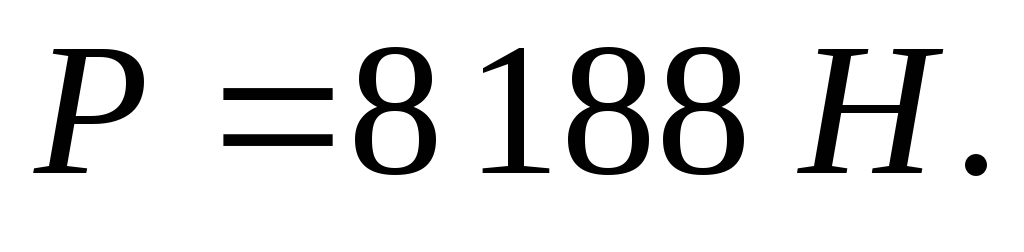
2.36.
Определить величину и направление
силы гидростатического давления воды
на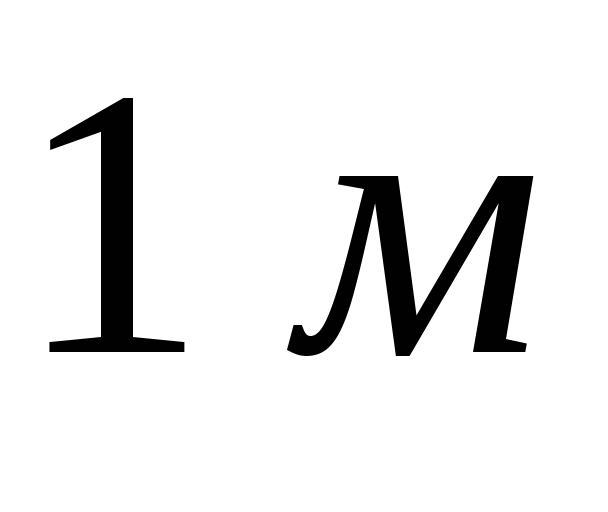 ширины вальцового затвора диаметром
ширины вальцового затвора диаметром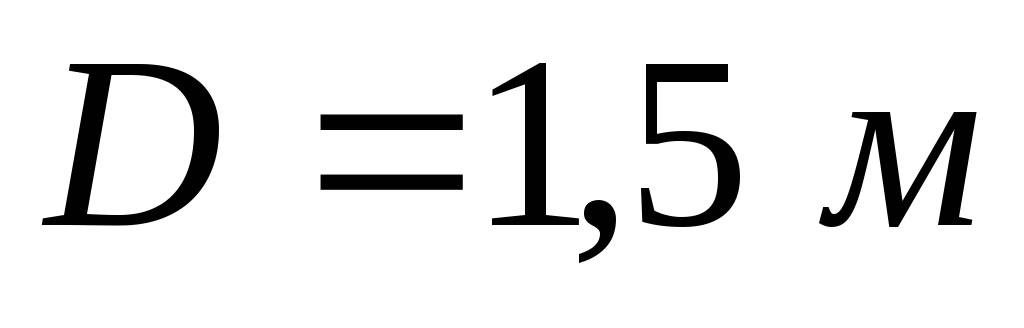 .
.
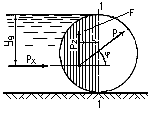
Решение.
1) Горизонтальная составляющая
2) Вертикальная составляющая
3) Суммарная сила давления
4) Составляющая Р х проходит на расстоянии у д от свободной поверхности:
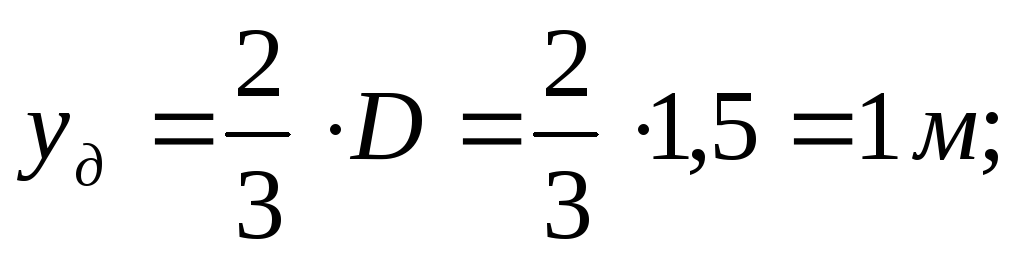
составляющая
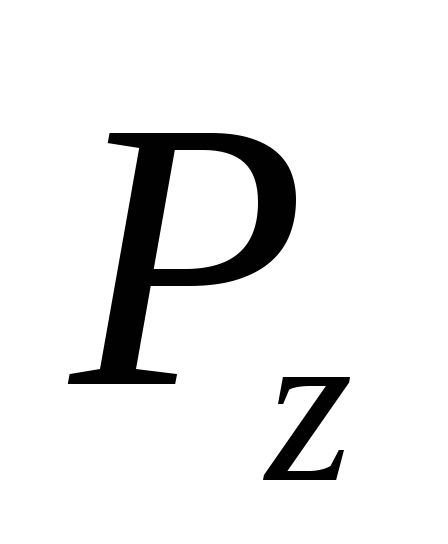 проходит на расстоянии
проходит на расстоянии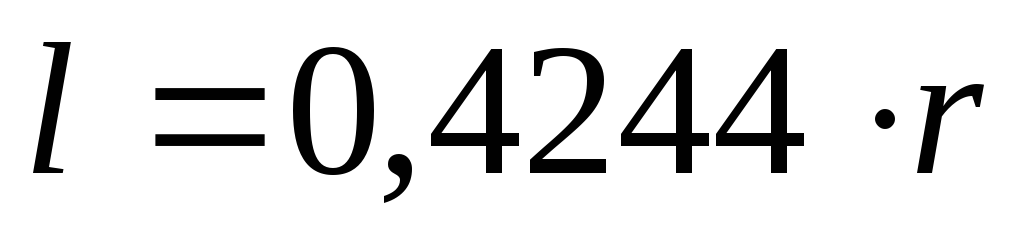 от линии
от линии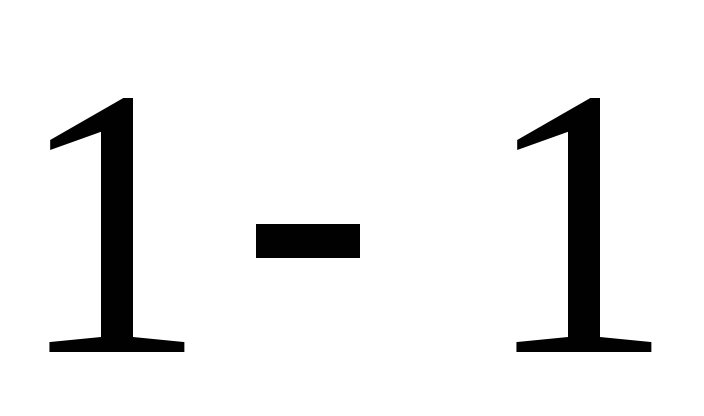 ,
равном
,
равном
5) Равнодействующая Р
приложена в
точкеО
под углом к горизонту и проходит через центр
круга, причем
к горизонту и проходит через центр
круга, причем
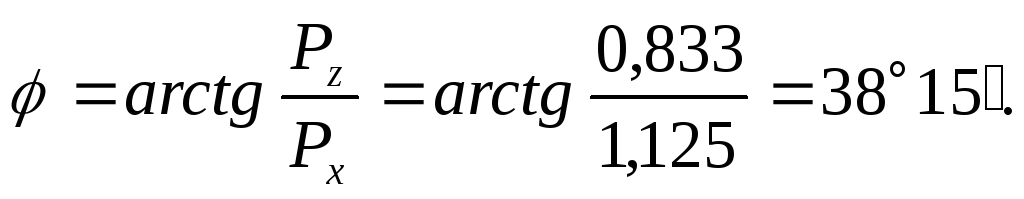
Ответ:
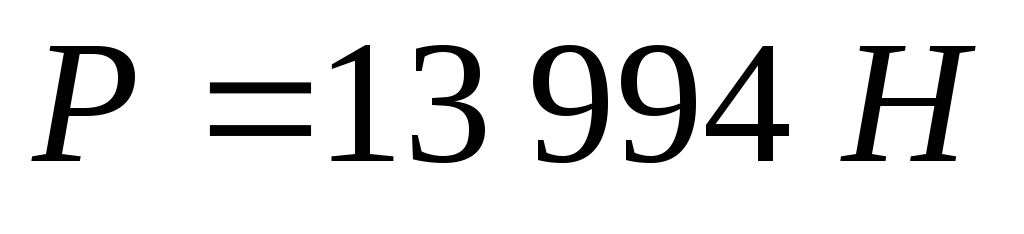 ;
;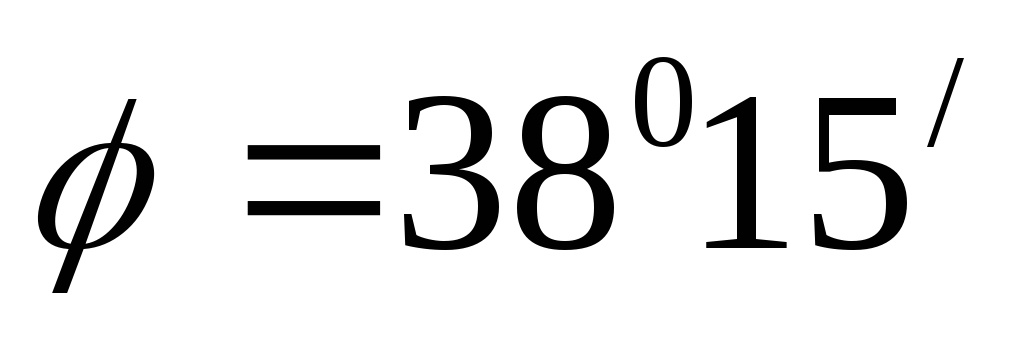 .
.
2.37.
Определить силу гидростатического
давления воды на 1м
ширины вальцового
затвора диаметром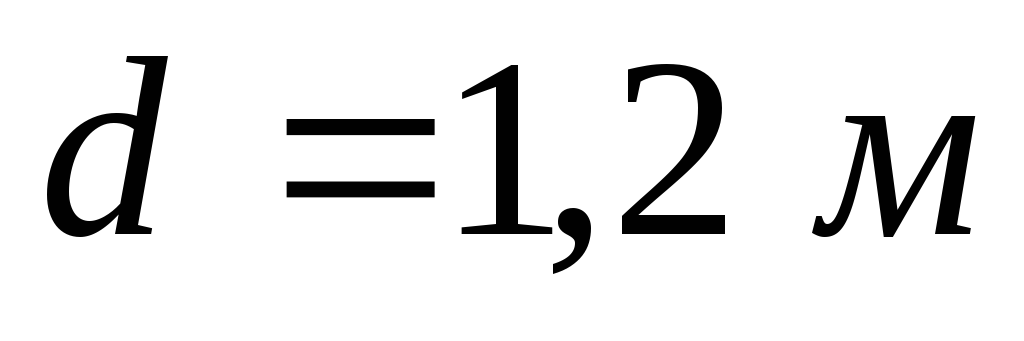 при
при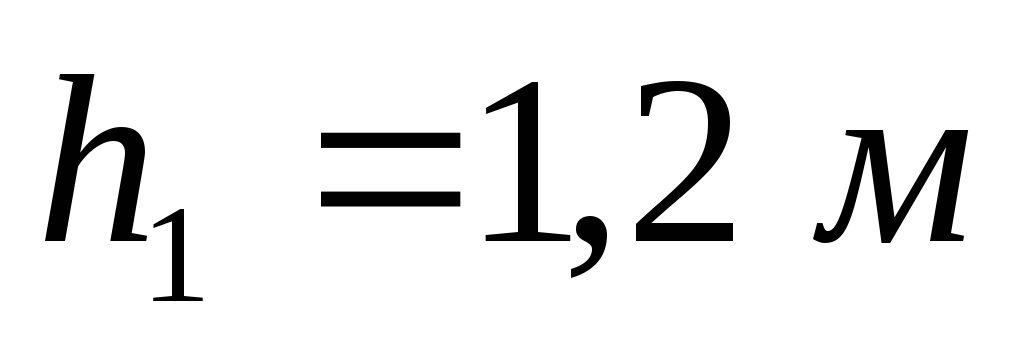 и
и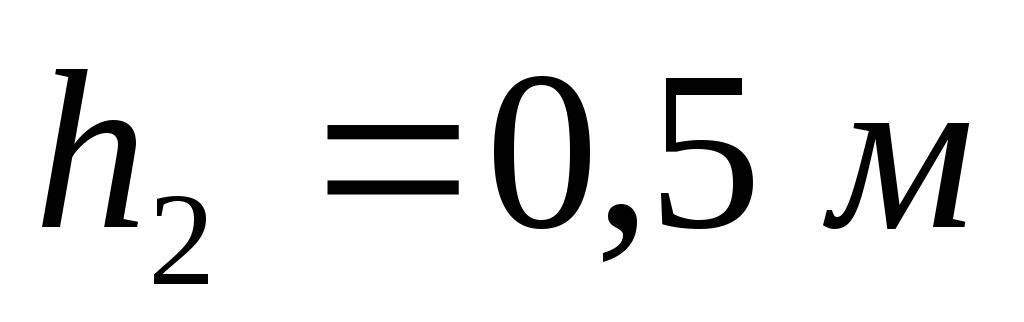 .
.
Решение. 1) Горизонтальная составляющая силы давления воды слева
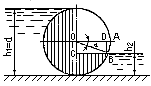
2) Вертикальная составляющая силы давления воды, равная весу жидкости в объеме тела давления (на рисунке заштриховано):
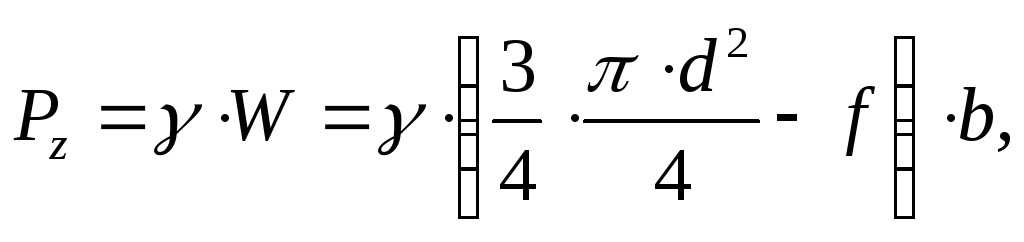
где
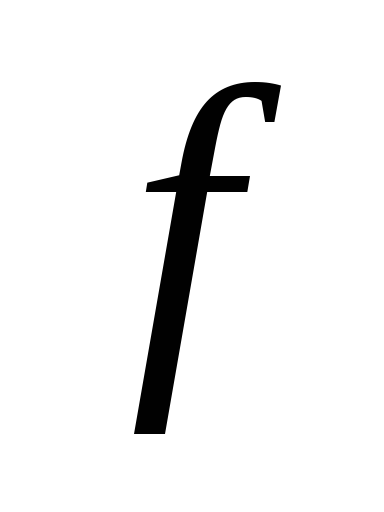 - площадь фигуры
- площадь фигуры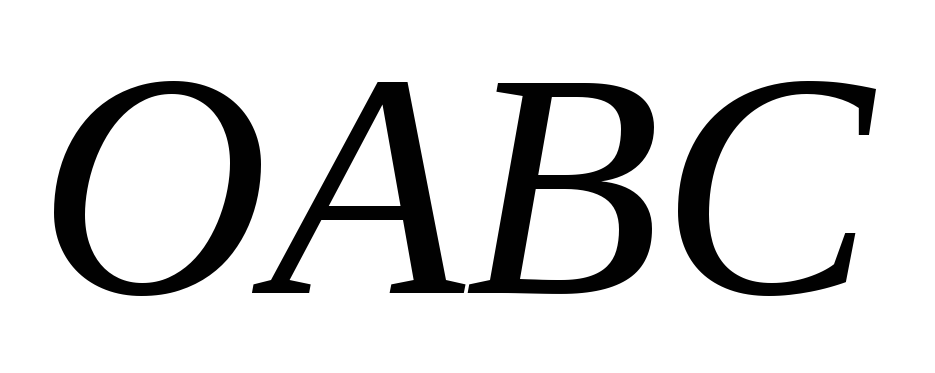 ,
для определения которой рассмотрим
треугольник
,
для определения которой рассмотрим
треугольник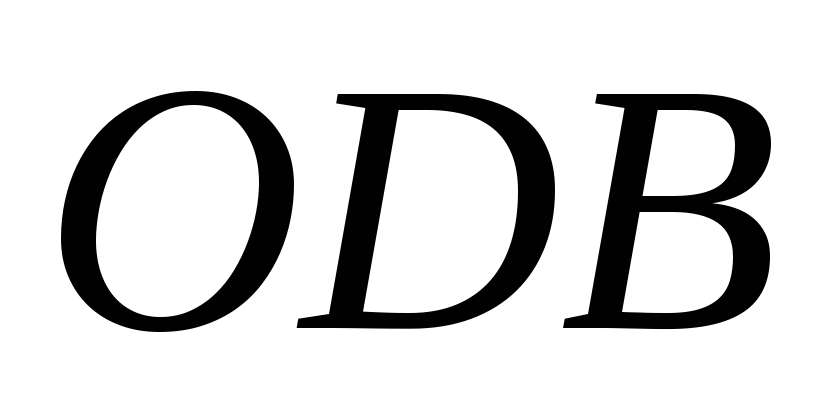 :
:
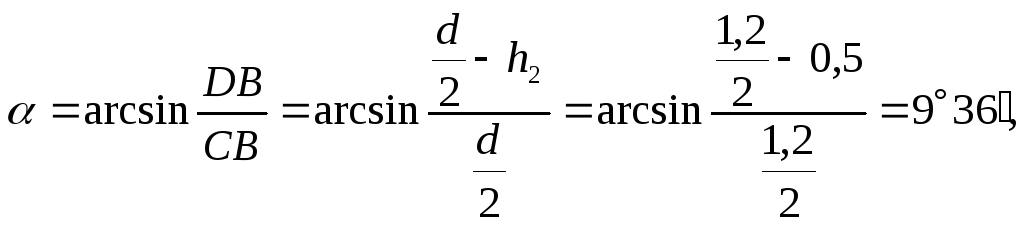
3) Суммарная сила давления
4) Угол наклона силы Р
к горизонту
определяется по тангенсу угла
 :
:
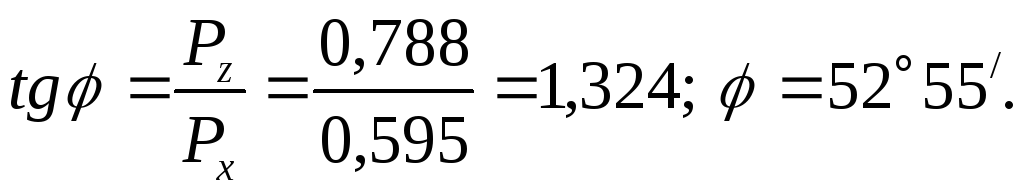
Ответ:
2.38.
Определить силу давления воды
на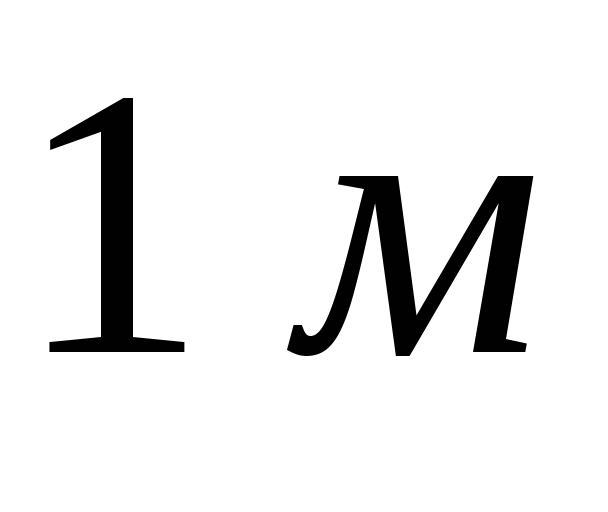 ширины затвора, перекрывающего канал
между двумя смежными камерами, если
глубина воды в левой камере
ширины затвора, перекрывающего канал
между двумя смежными камерами, если
глубина воды в левой камере![]() в правой
в правой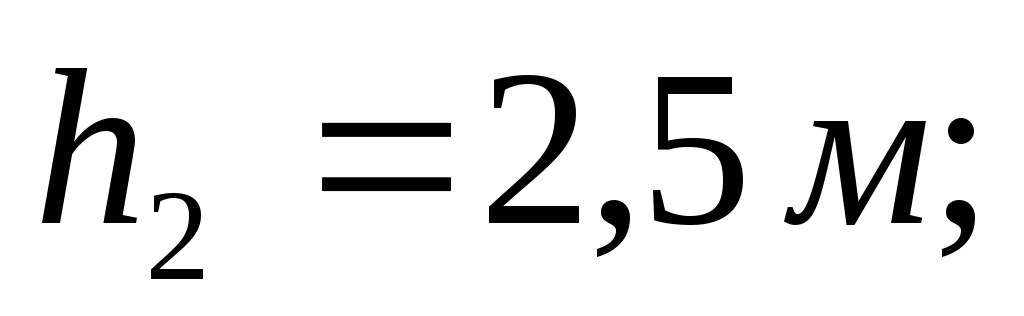
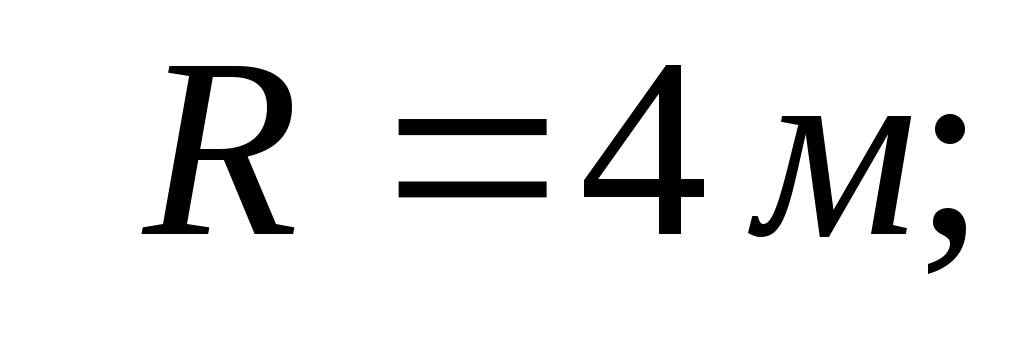
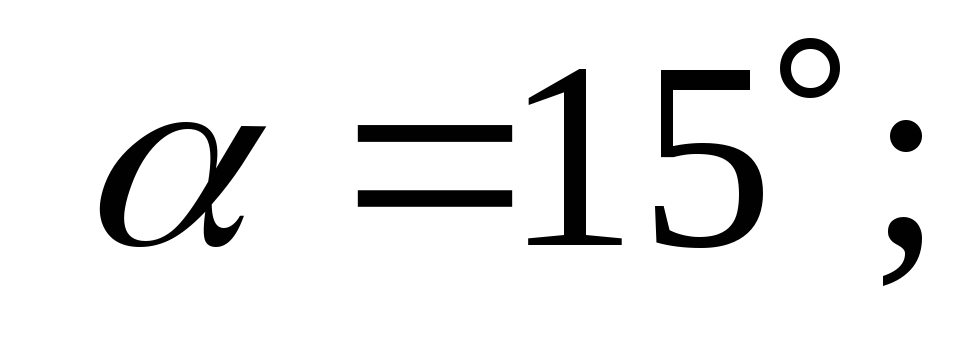
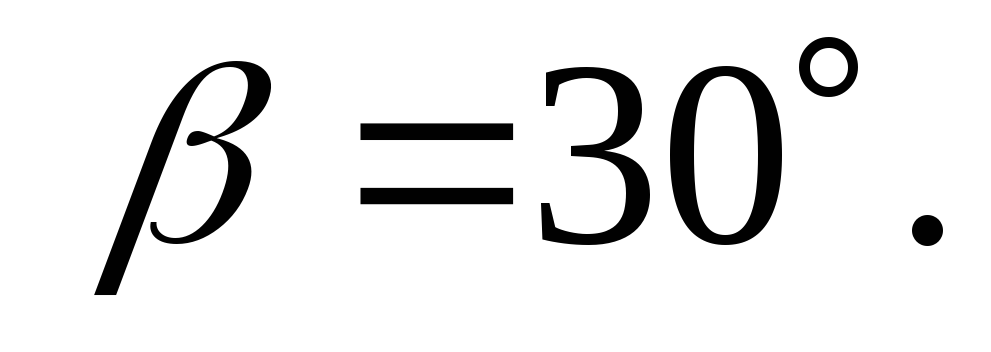
Решение. 1) Горизонтальная составляющая силы давления воды на затвор слева
2) Вертикальная составляющая P z равна весу жидкости в объеме тела давления (на рисунке заштриховано):
где d – длина основания тела давления;
b
= 1м
– его
ширина. Для определения рассмотрим треугольникиАВО
иАВС
:
рассмотрим треугольникиАВО
иАВС
:
3) Суммарная сила давления на затвор
Сила Р
проходит через шарнирО
под углом к горизонту, причем
к горизонту, причем
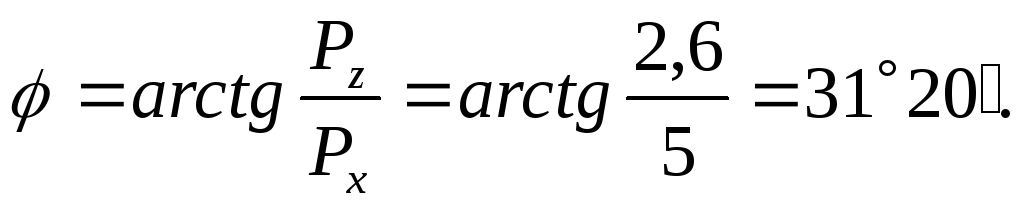
Ответ:
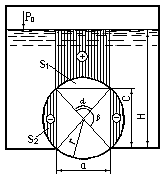
2.39.
Цилиндр радиусом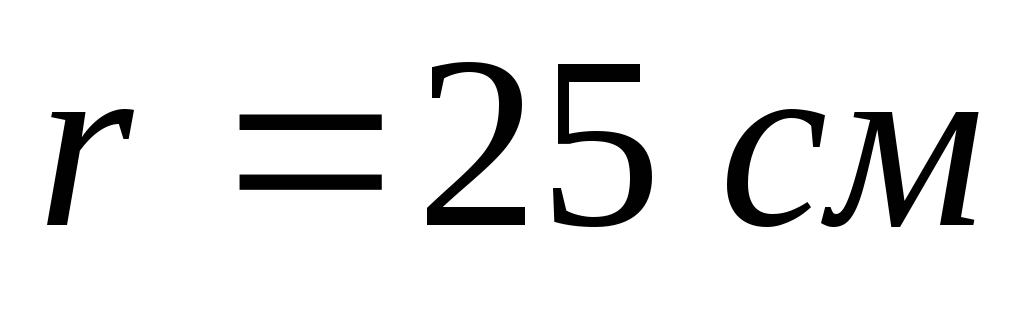 и длиной
и длиной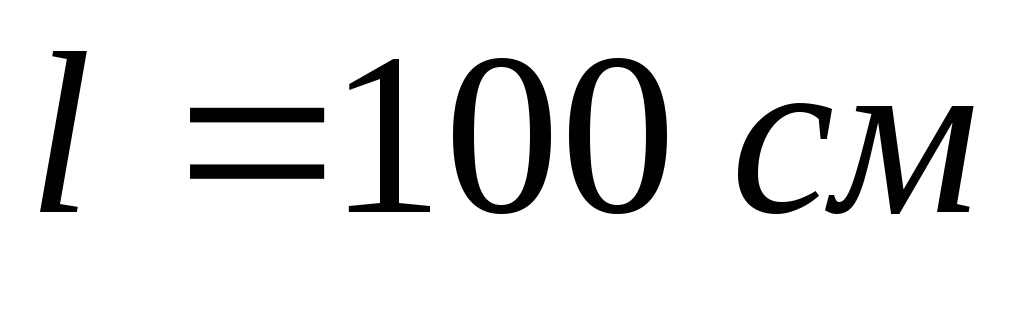 перекрывает отверстие в дне резервуара
размерами
перекрывает отверстие в дне резервуара
размерами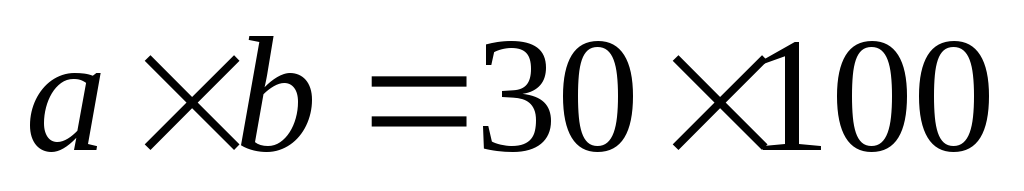 см.
Определить: силу давления воды на цилиндр
при
см.
Определить: силу давления воды на цилиндр
при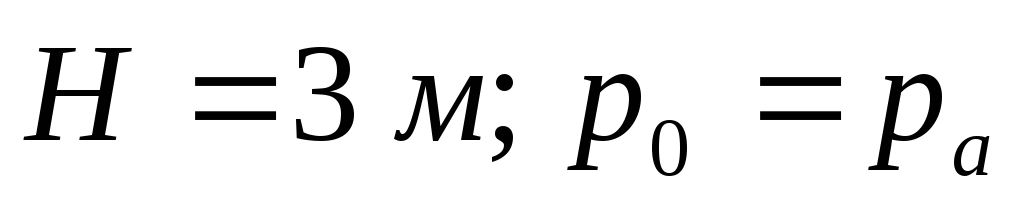 .
.
Решение. 1) Горизонтальная составляющая силы давления воды на цилиндр равна нулю, так как и на его основания и на продольные вертикальные проекции действуют соответственно равные и противоположно направленные силы.
2) Вертикальная составляющая равна весу жидкости в объёме тела давления (на рисунке заштриховано):
Из рисунка видно, что
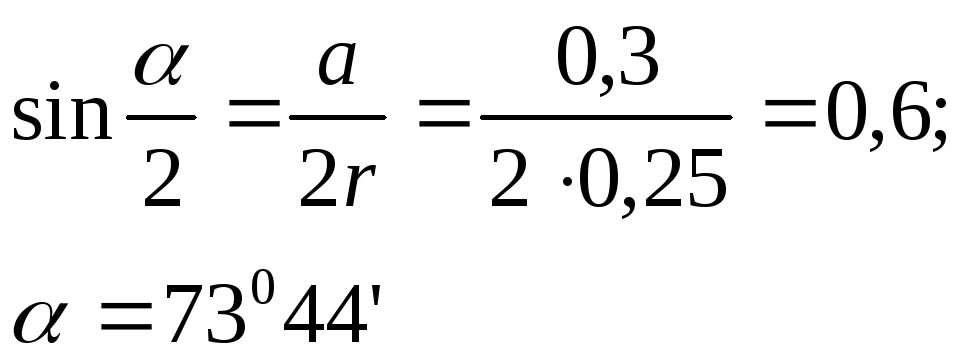
Тогда площади сегментов s 1 иs 2 определяются по формулам
Ответ:
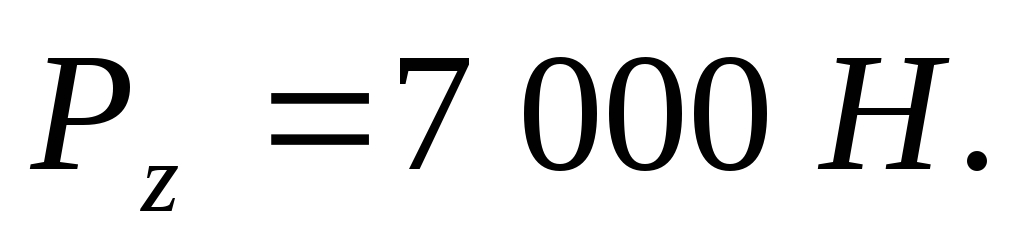
2.40
. На горизонтальной плите установлен
стальной сосуд без дна в форме усеченного
конуса с толщиной стенки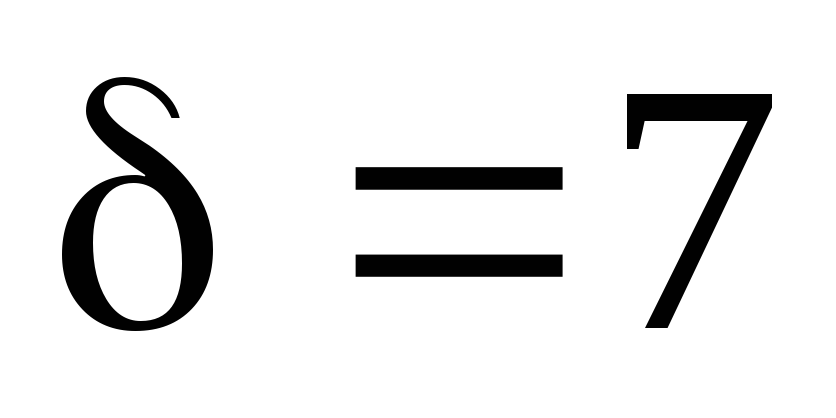 мм. Определить при каком уровне воды в
сосудеhон оторвется от
плиты, если известныD=2
м,d=0,5 м, Н=2 м.
мм. Определить при каком уровне воды в
сосудеhон оторвется от
плиты, если известныD=2
м,d=0,5 м, Н=2 м.
Решение: Сосуд может оторваться от плиты в том случае, если вертикальная сила гидростатического давления воды на
наклонные (конические) стенки сосуда превысит силу веса самого сосуда. Составим уравнение равновесия этих сил:
G=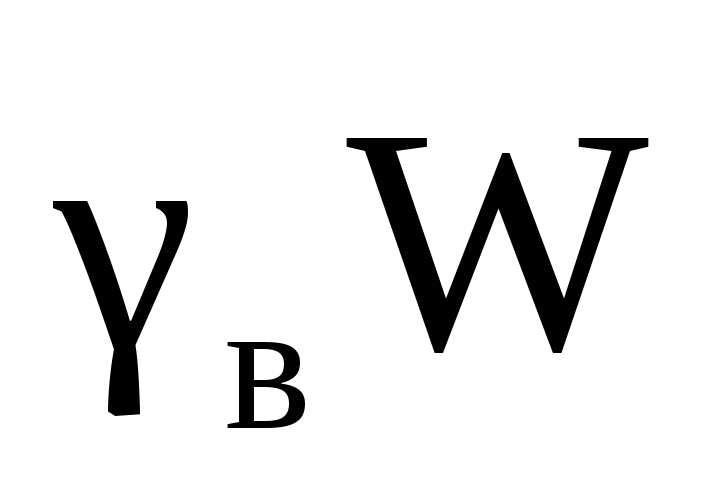 т.д. ;
т.д. ;
Где G=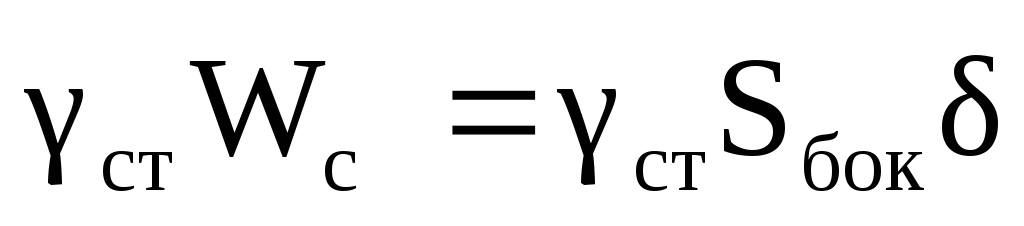 ,
,
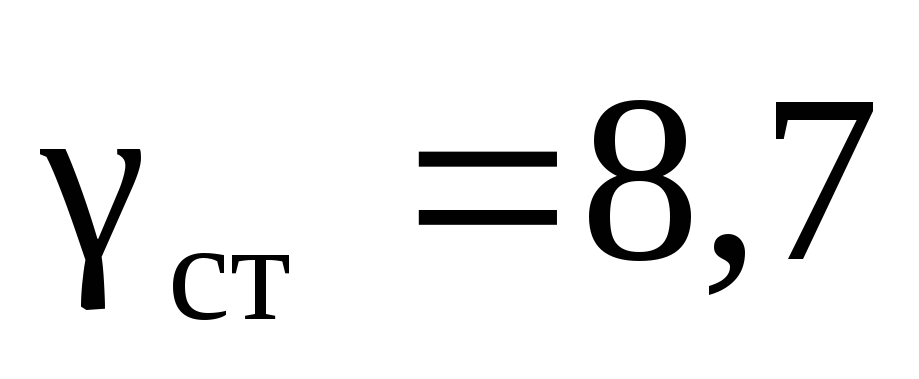 т/м 3 =8,5
т/м 3 =8,5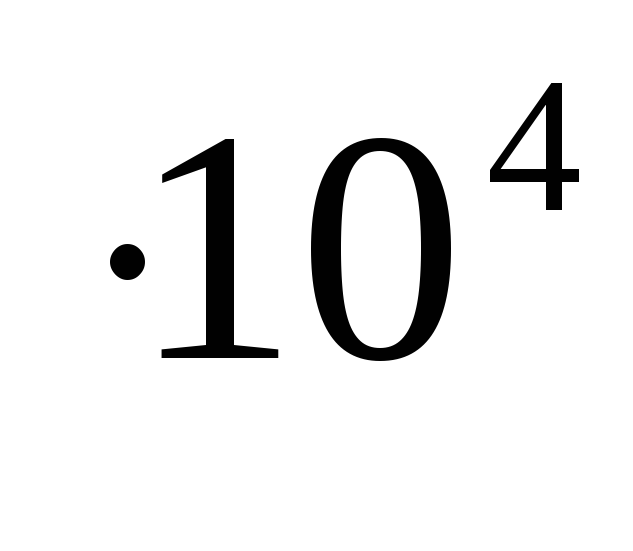 Н/м 3 ;
Н/м 3 ;
S бок =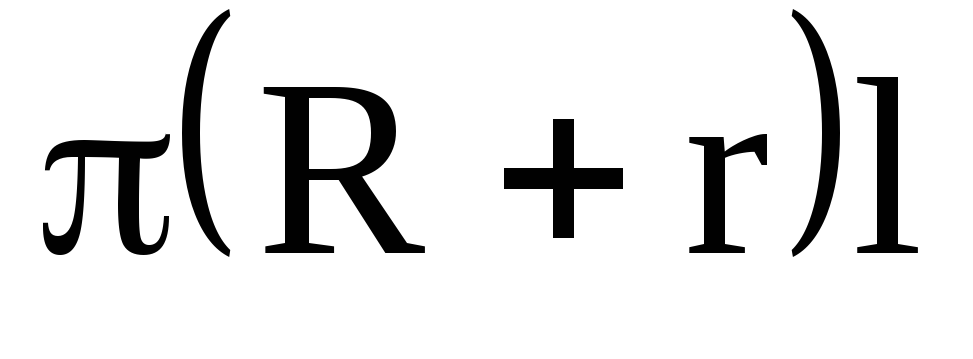 -
боковая поверхность конуса;
-
боковая поверхность конуса;
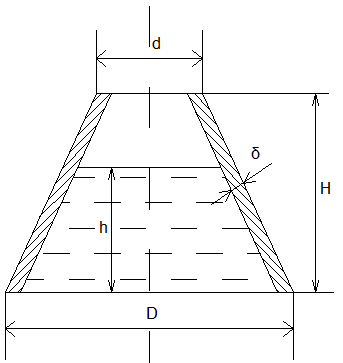
l-длина образующей:
l = 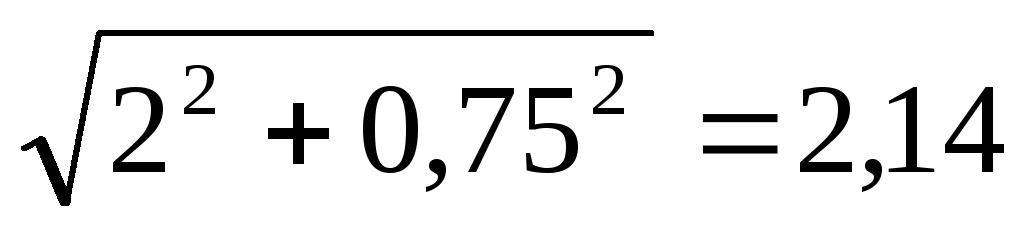 м,
м,
тогда S бок =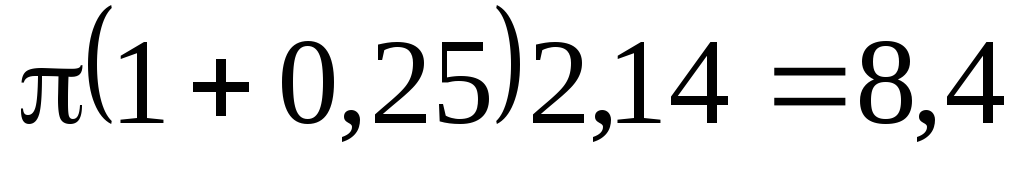 м 2 .
м 2 .
Вес сосуда равен G =8,4 Н.
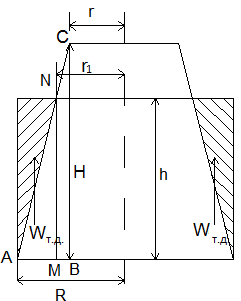
Тело давления –это заштрихованная фигура, которая создает вертикальную отрывающую силу F z .
Запишем объем тела давления:
W т.д.= 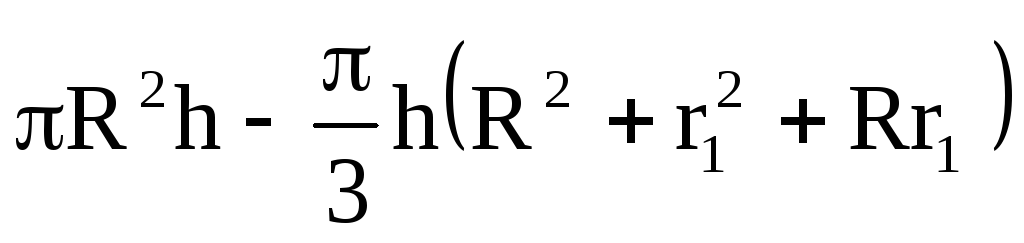 ,
(
,
( )
)
где r 1 –является неизвестной величиной. Выразим ее через глубину воды в сосудеh.
Для этого cоставим пропорцию для подобных треугольников АВС и АМN:
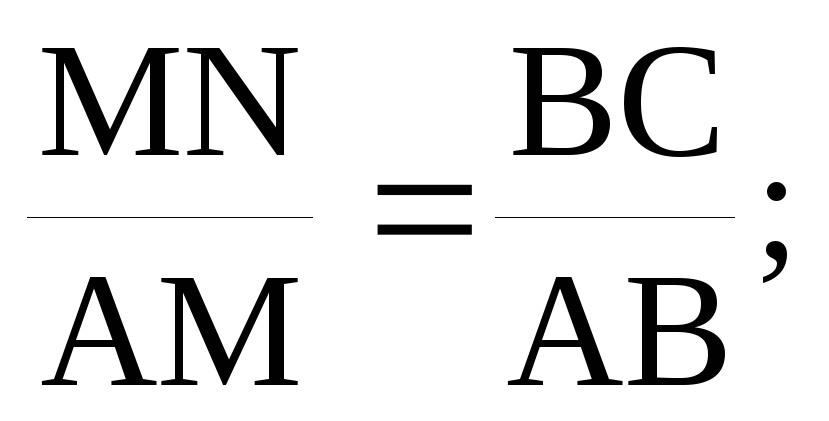
Тогда 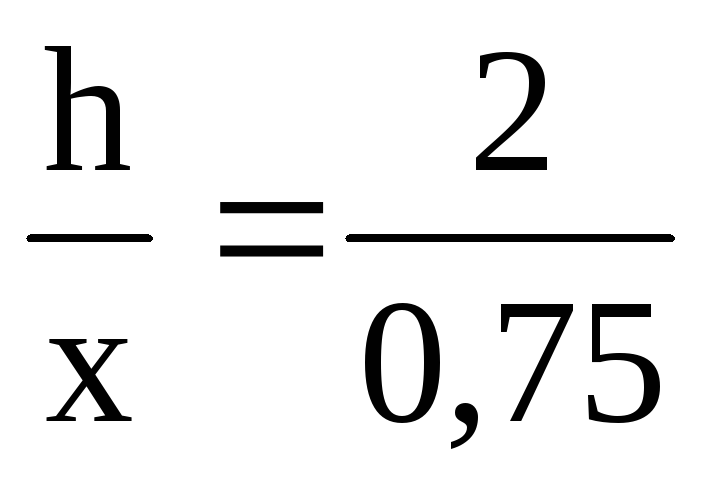 ,
откуда х =
,
откуда х = 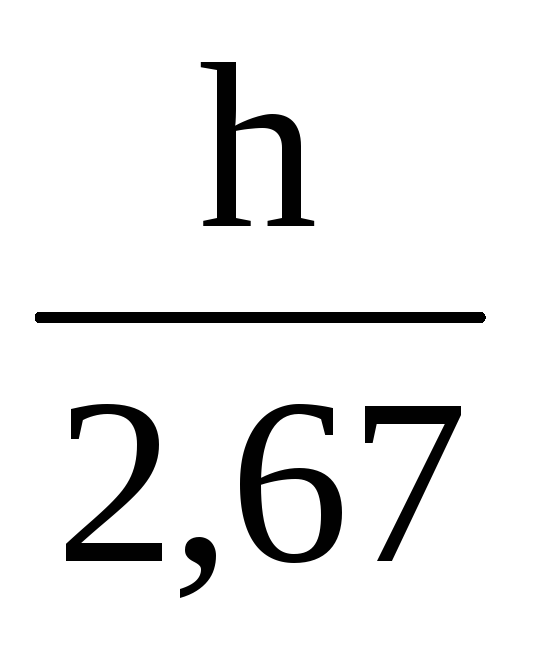 .
.
Тогда d 1=2 r 1= D - 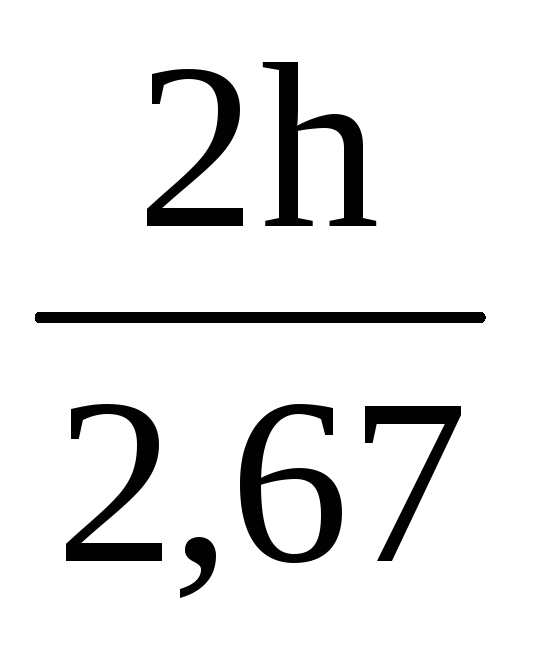 .
.
Теперь выразим радиус r 1:
r 1= 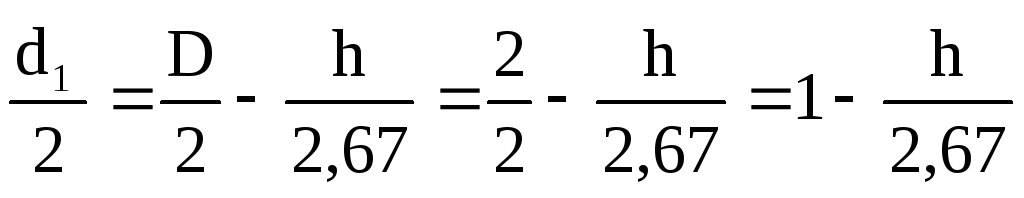 .
.
Подставим значение r 1 в уравнение ( ):
):
W т.д.= 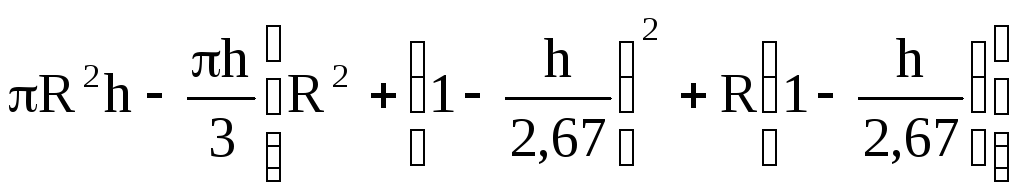 ,
,
Раскрываем скобки, приведем подобные элементы, получим:
1,04h-0,4h 2 -0,15h 3 .
Учитывая, что 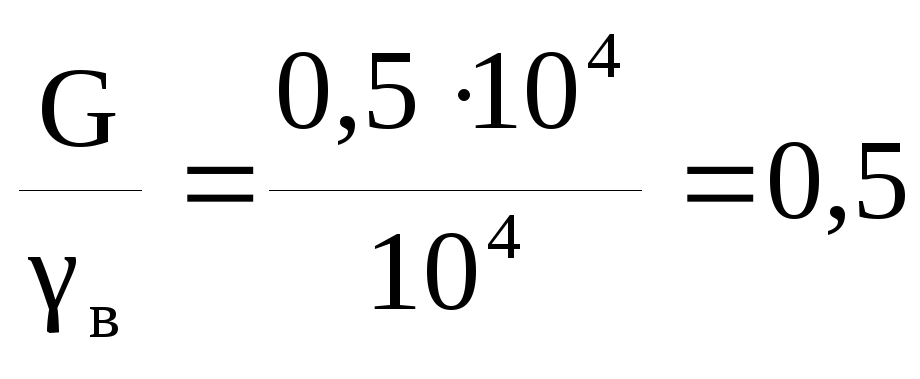 м 3 ,
м 3 ,
Окончательно получаем:
0,15h 3 -0,4h 2 +1,04h-0,5=0
Способом подстановок “h” в это уравнение найдем значение:
Проверка: 0,15 ;
0,6333-0,635 0.
0.
Ответ: h=0,58 м.
2.41 . Определить силу натяжения троса, удерживающего криволинейный затвор, представляющий собой четверть кругового цилиндра радиусаR=1 м, перекрывающего канал прямоугольного сечения ширинойb=3 м. Глубина наполнения канала водойH=2 м.
Решение: Для определения силы натяжения троса составим
уравнение моментов всех сил, действующих на затвор, относительно
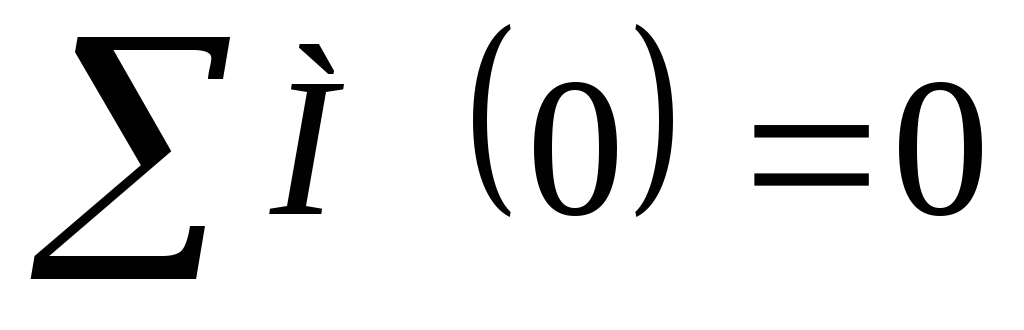 ;
;
ТR=P z l p +P x l b .
Для чего найдем составляющие Р х и Р z
силы гидростатического давления на криволинейный
(цилиндрический) затвор:
Р x =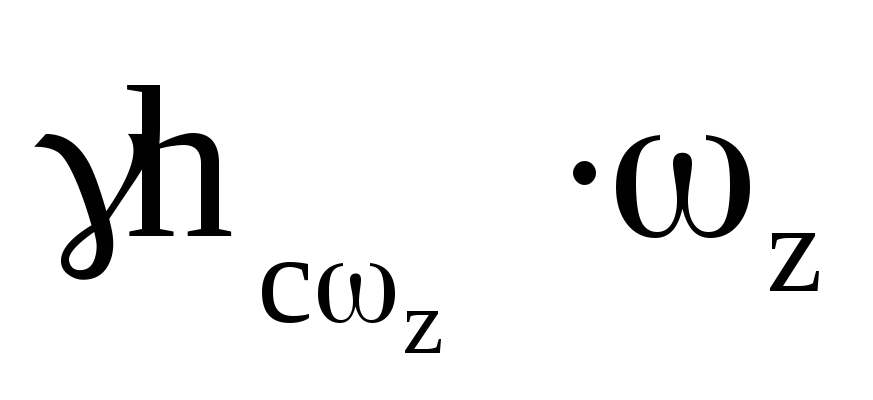 =10 4
=10 4 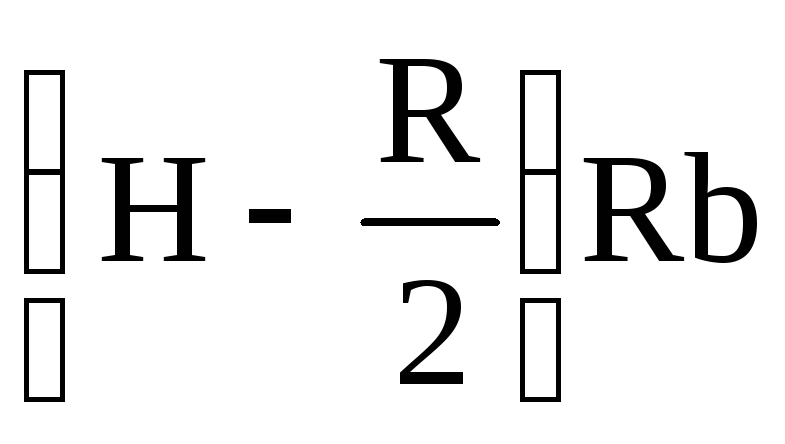 =
=H.
=
=H.
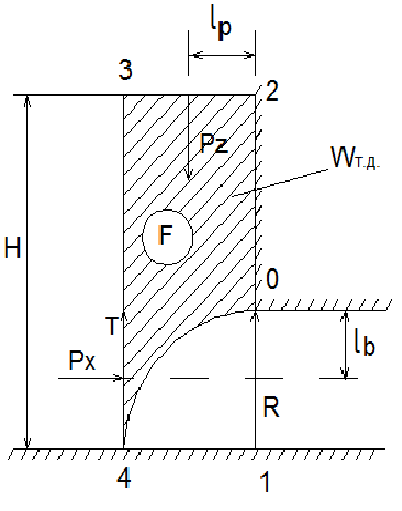
Точка приложения этой составляющей находится на расстоянии l b от оси шарнира 0:
L b =l д -(H-R),
L д =l c +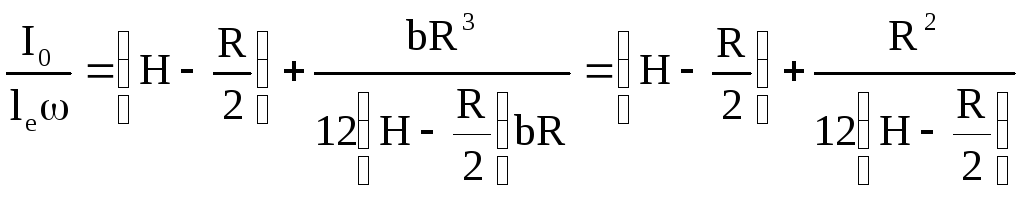 ;
;
Составляющая P z находится через объем тела давленияW т.д. :
P z =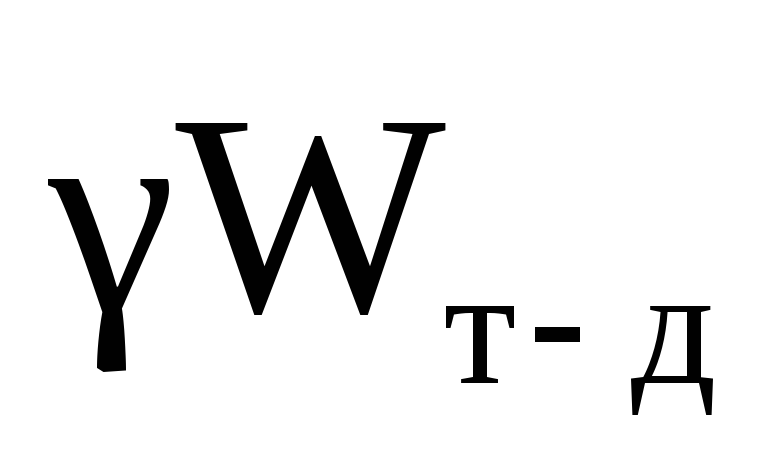 ,
,
где W т.д. =![]() .
.
Тогда P z =H.
Линия действия этой вертикальной составляющей проходит через центр тяжести фигуры 1-0-2-3-4. Расстояние l р центра тяжести фигуры 1-0-2-3-4 от линии 0-2 равно статическому моменту этой фигурыSотносительно линии 1-0-2, поделенному на площадь фигурыF(причем расстояние центра тяжести четверти круга 1-0-4 от линии 1-0-2 равно е=0,4244R).
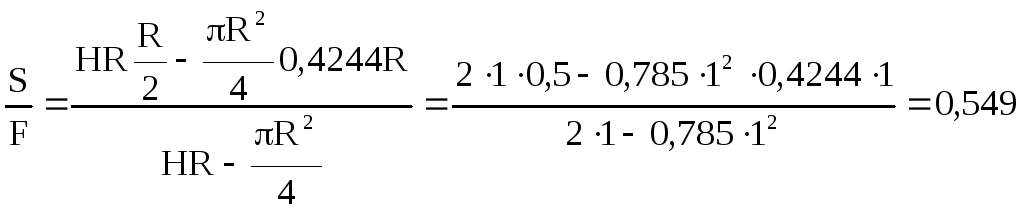 м.
м.
Тогда Т= H.
Ответ:
Т=4,52 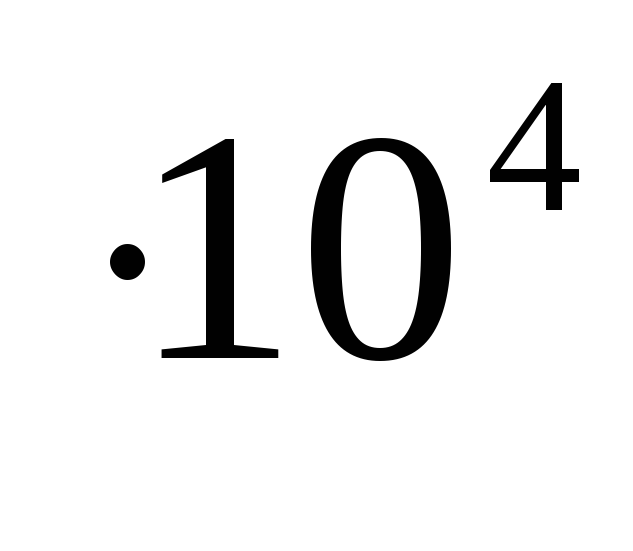 Н.
Н.
2.42. Найти величину и направление силы гидростатического давления воды на 1м ширины криволинейного затвора, если известны
Решение:
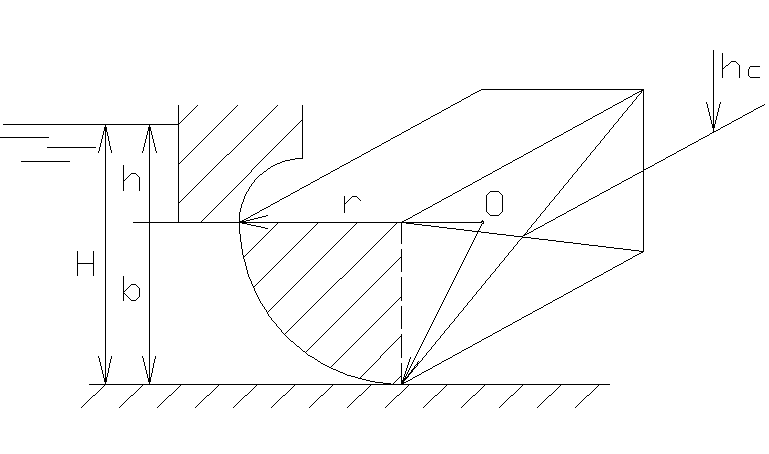 Результирующая
сила гидростатического давления равна
Результирующая
сила гидростатического давления равна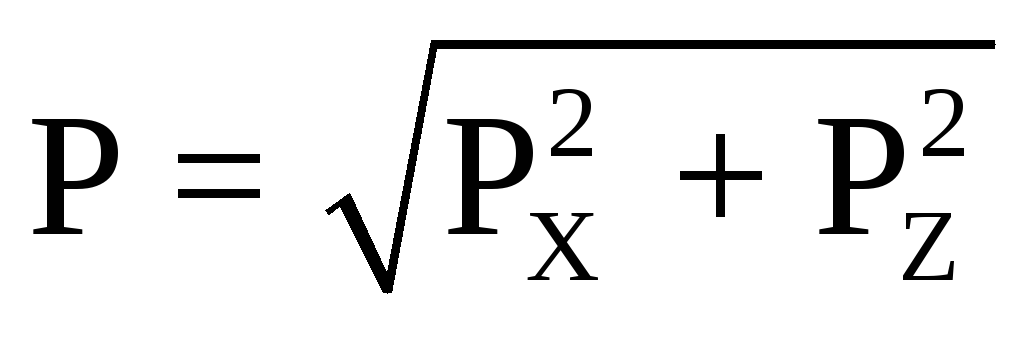 .
Найдём составляющие этой силы
.
Найдём составляющие этой силы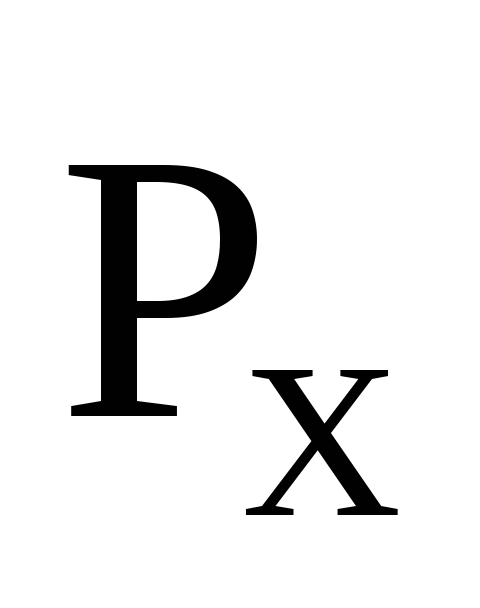 и
и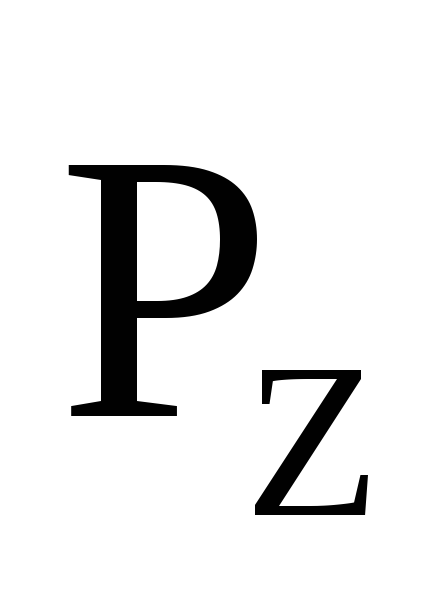 :
:
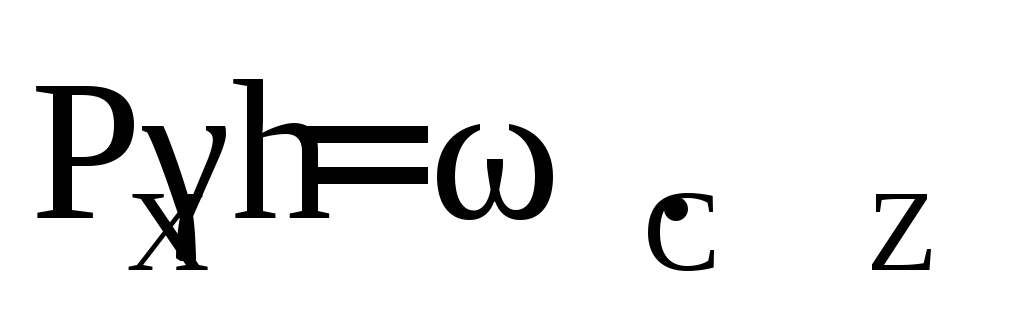
Найдём параметры затвора:
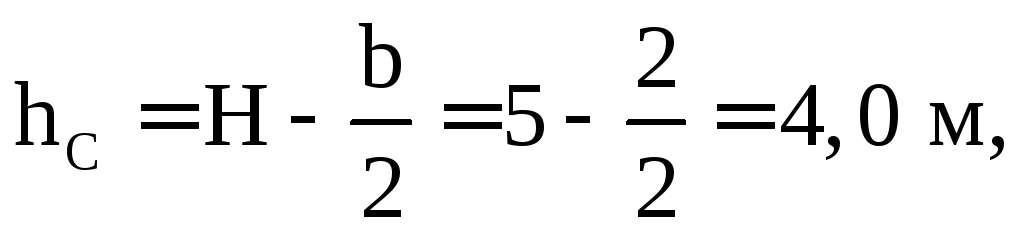
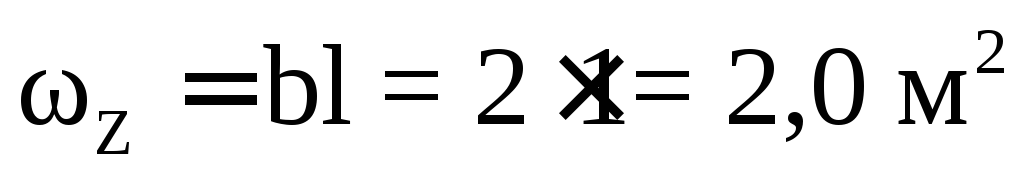
Тогда горизонтальная составляющая равна:
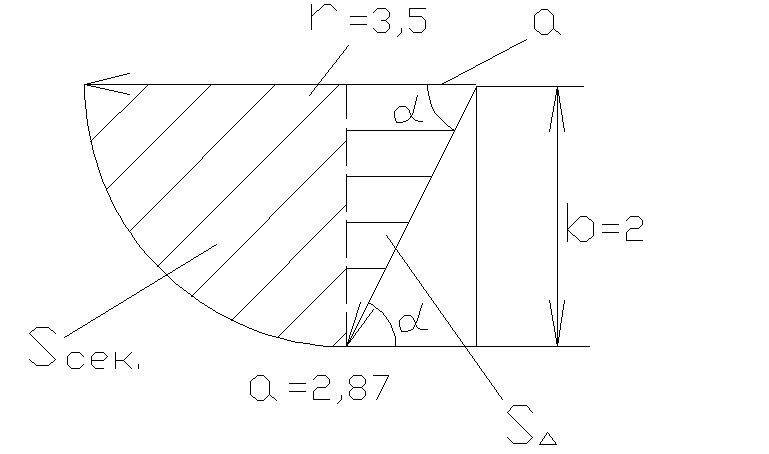
Найдём вертикальную составляющую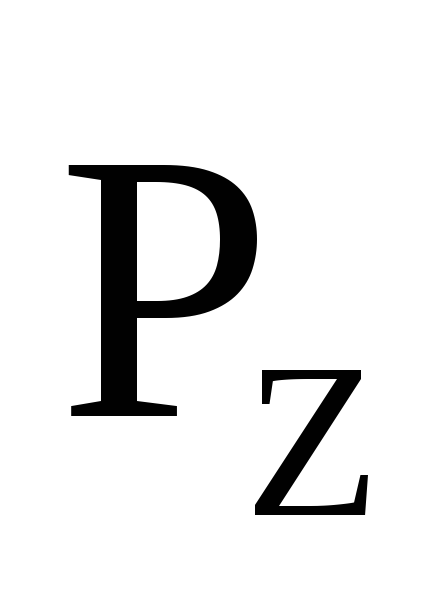 ,
для чего вычислим объём тела давления:
,
для чего вычислим объём тела давления: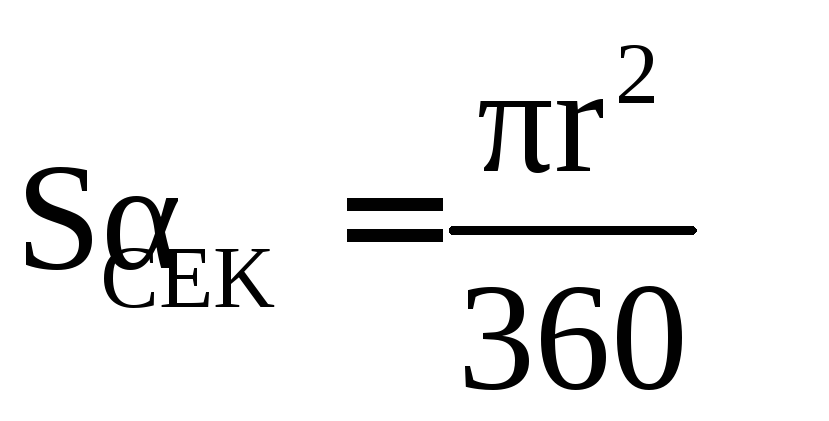 ,
,
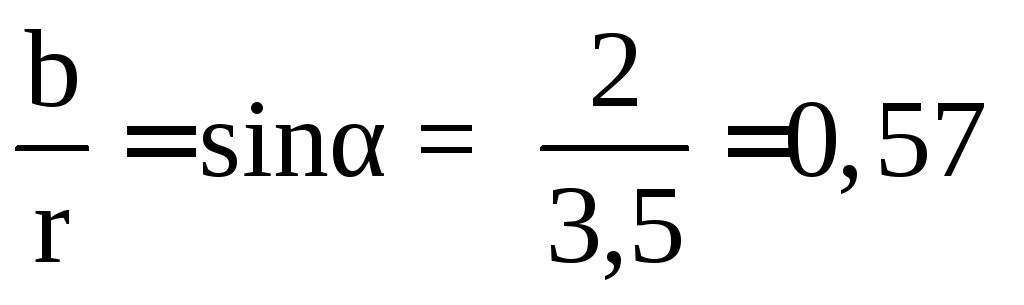
 ;
;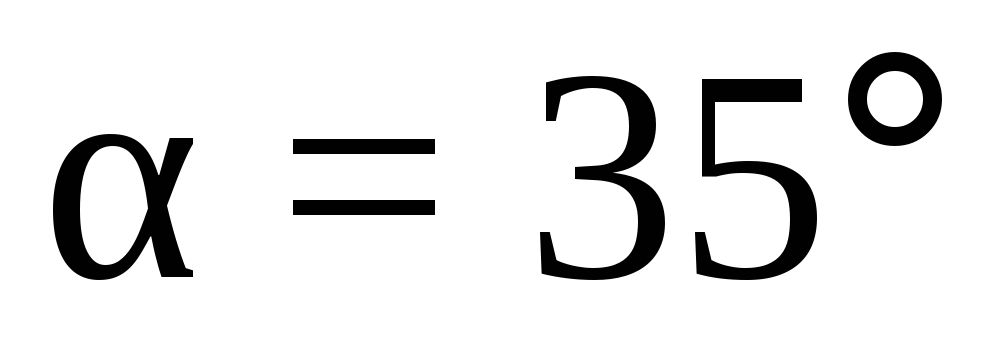 ;
;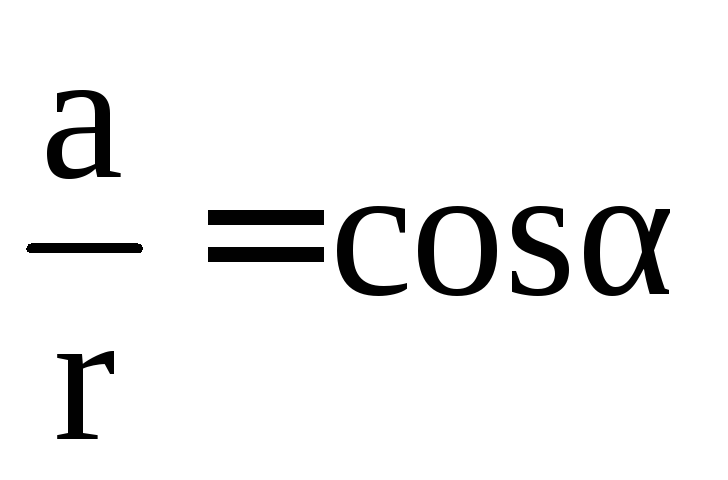 ;.
;.
Найдём площадь треугольника:
S ∆ 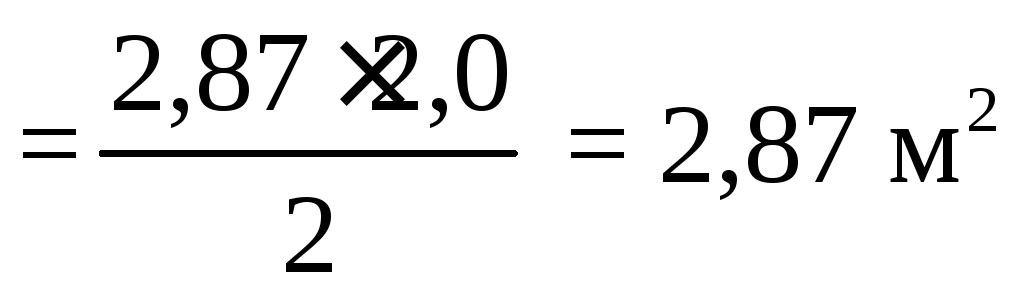 .
.
Площадь сектора составит:
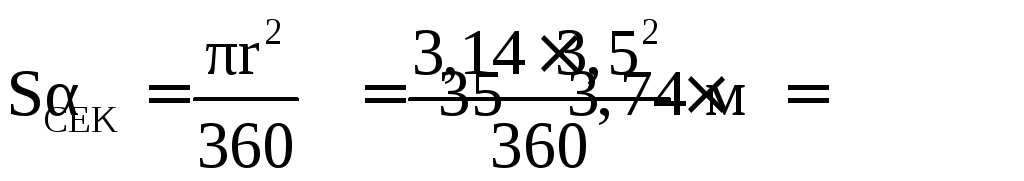 .
.
Площадь тела давления:
 .
.
Тогда объём тела давления составит:
Полная сила гидростатического давления на затвор составит:
а направление этой силы определяется углом φ:
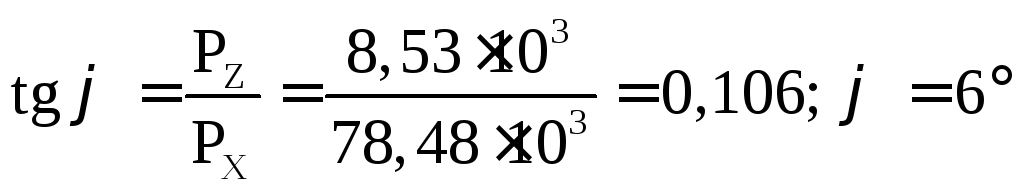 .
.
Ответ:
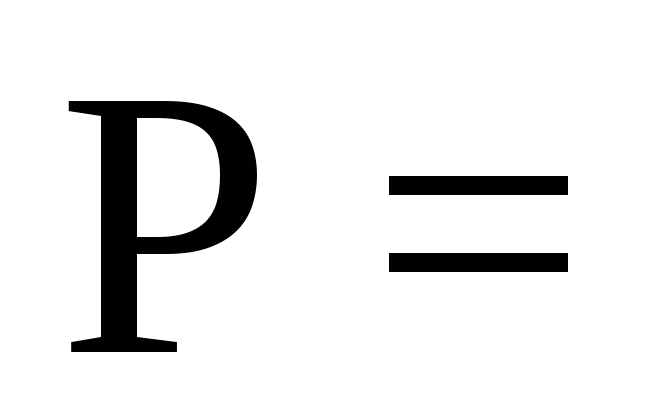
 ,
,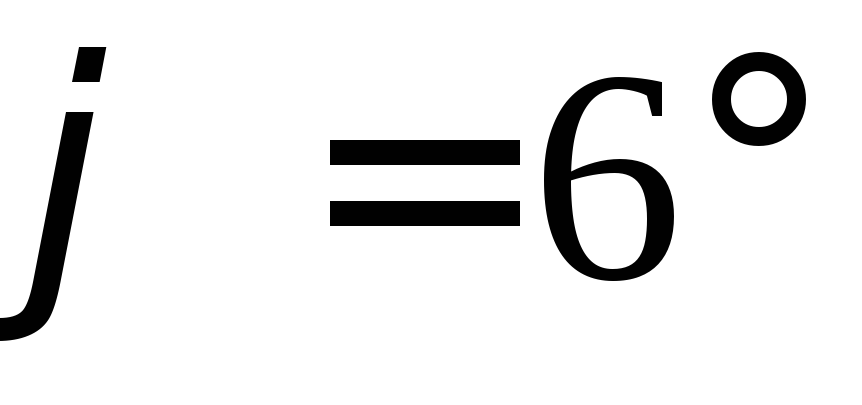 .
.
2.43.
Определить горизонтальную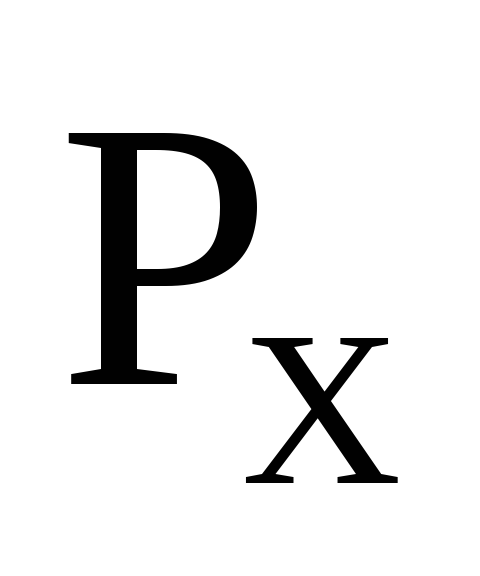 и вертикальную
и вертикальную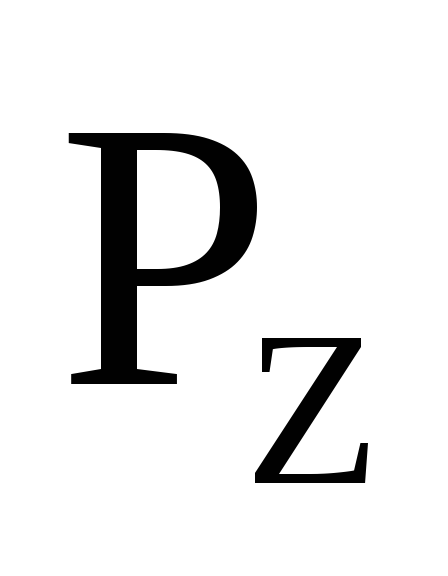 составляющие силы давления воды на
горизонтальный цилиндр диаметромd= 30 см, который вставлен чepeз
отверстие в наклонной стенке (α = 30º)
внутрь резервуара на расстоянииl= 0,8 м. Уровень воды над осью цилиндра Н
= 1,0 м.
составляющие силы давления воды на
горизонтальный цилиндр диаметромd= 30 см, который вставлен чepeз
отверстие в наклонной стенке (α = 30º)
внутрь резервуара на расстоянииl= 0,8 м. Уровень воды над осью цилиндра Н
= 1,0 м.
P
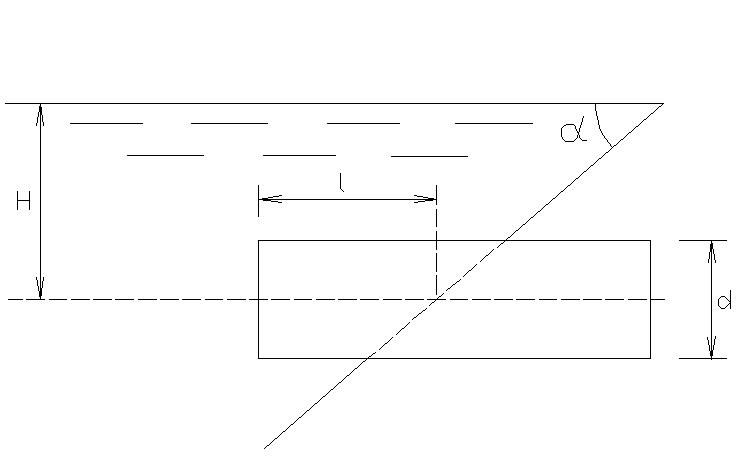 ешение:
ешение:
Горизонтальная составляющая силы давления на цилиндр определяется так:
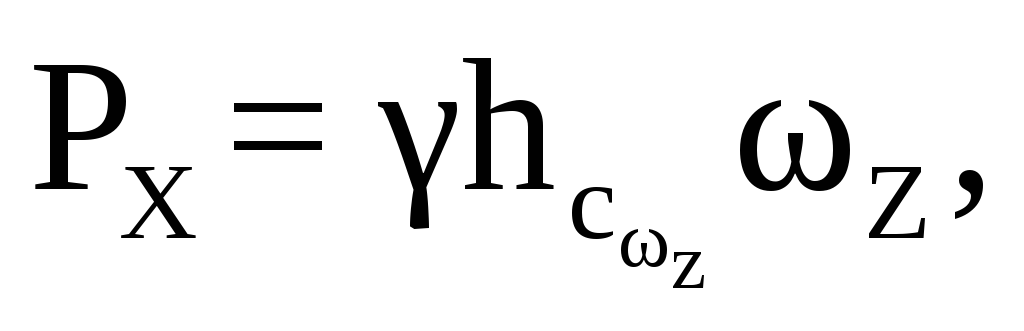 где
где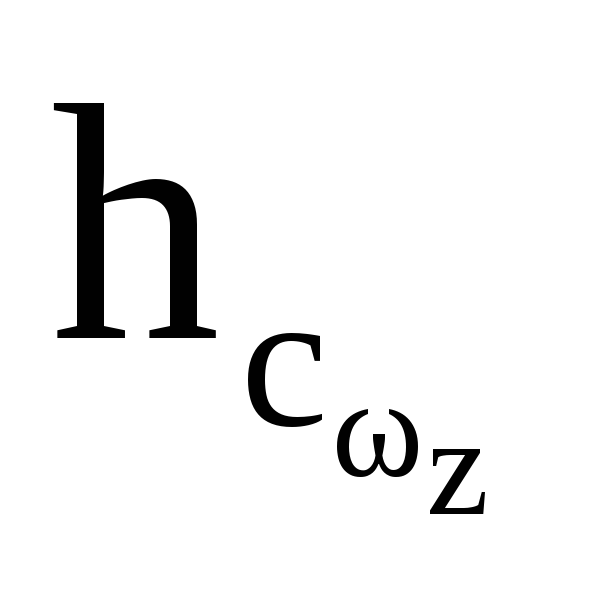 -
заглубление центра тяжести
-
заглубление центра тяжести
вертикальной проекции криволи-
нейной поверхности, т.е.
 ,
,
 -
площадь вертикальной проекции цилиндра:
-
площадь вертикальной проекции цилиндра:

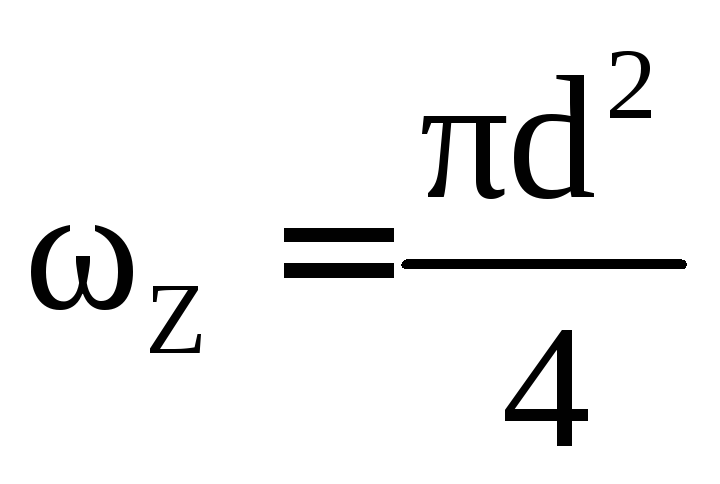 .
.
Вертикальная составляющая силы давления воды на цилиндр равна:
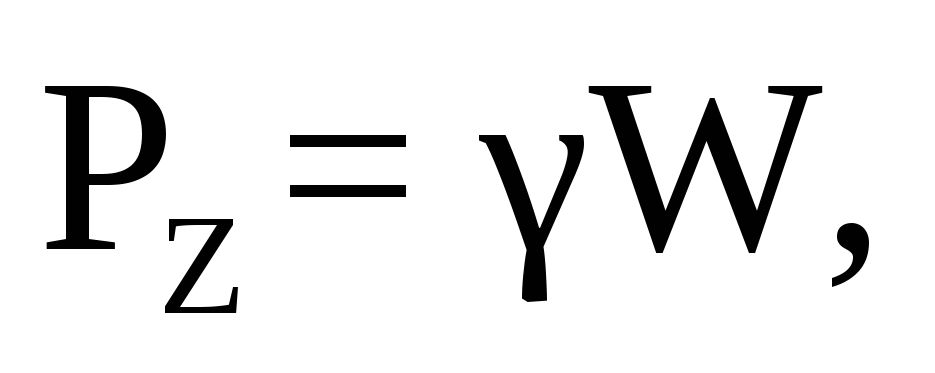
г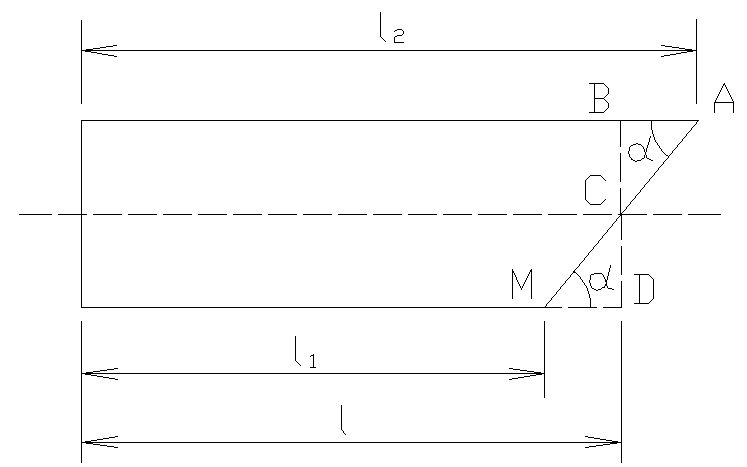 деW– объём тела давления,
который найдём из геометрии.
деW– объём тела давления,
который найдём из геометрии.
Рассмотрим ∆ АВС и ∆ МСD. Они равны,
так как АС = СМ =
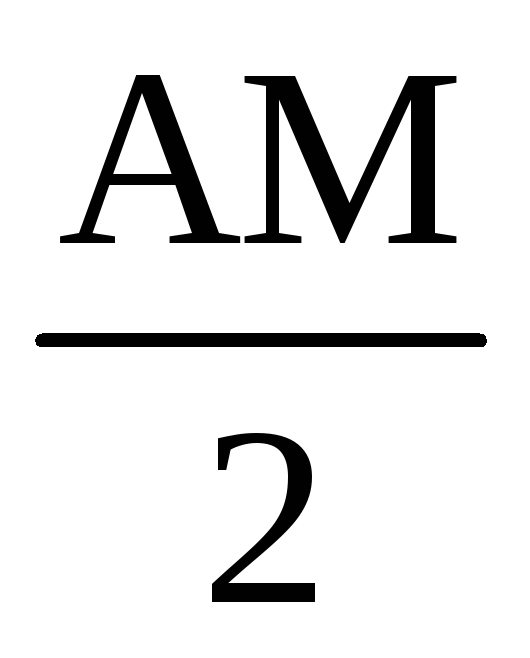 ;
ВС =CD=;
;
ВС =CD=;
Поэтому объёмы будут равны:
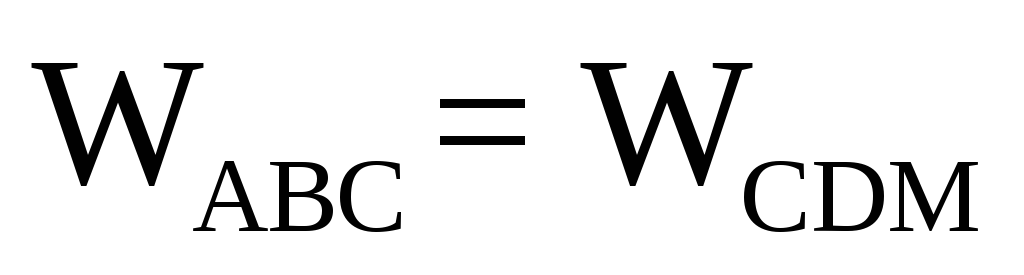
Тогда объём тела давления определяется так:
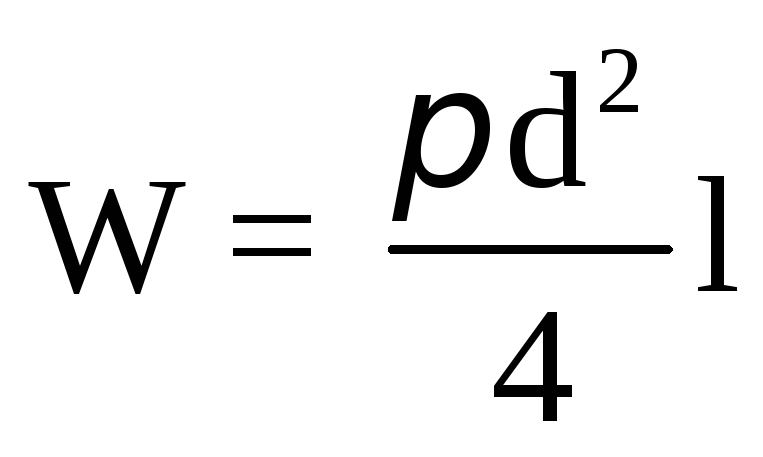 .
.
Либо объём тела давления найдём так. Из ∆ АВС:
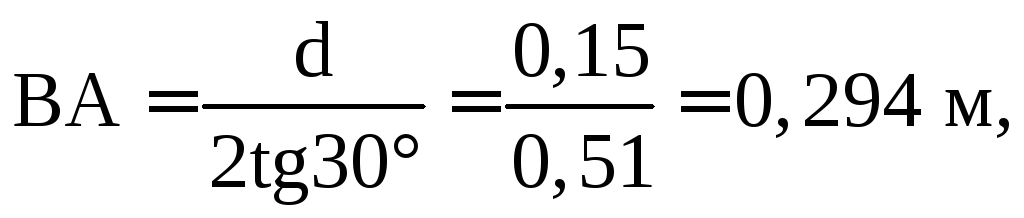
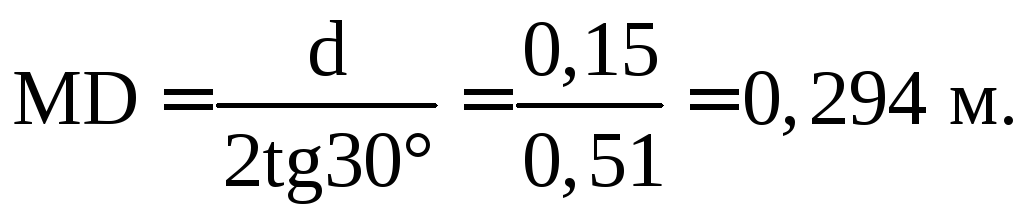
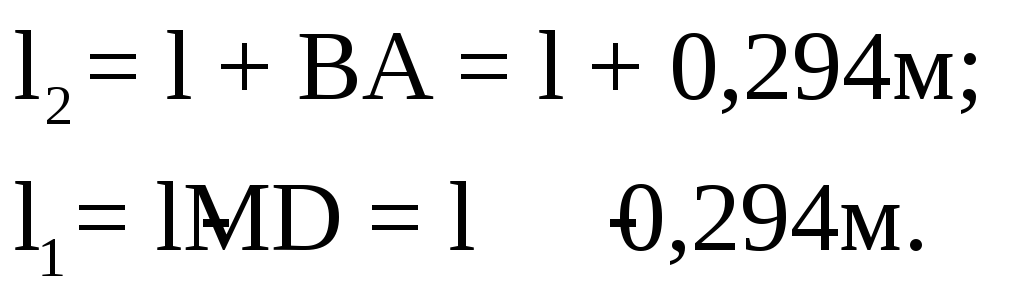
Окончательно:
Ответ: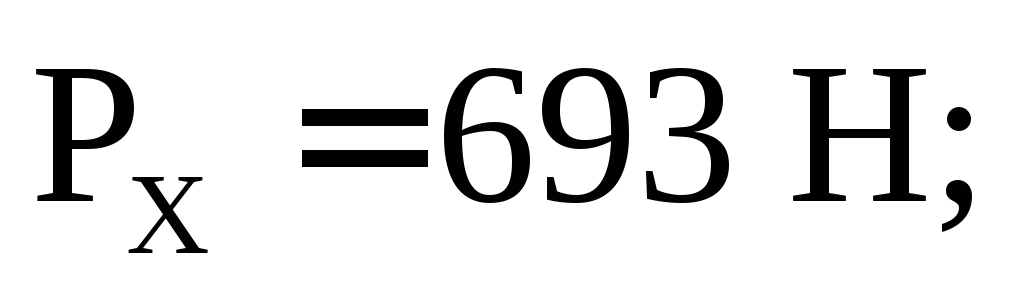
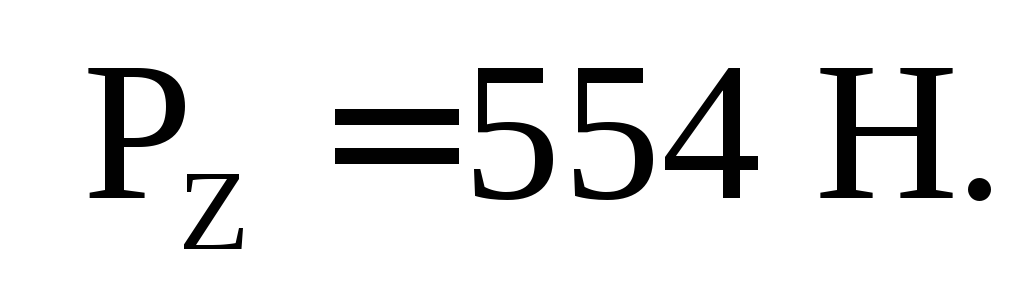
2.44. В прямоугольном окне вертикальной стенке установлен цилиндрический затвор (270º) диаметромD= 100 см и длинойb= 2,0 м. Определить усилие Р на цапфы и момент М от воздействия жидкости на затвор. Весом затвора пренебречь. Напор над осью крепления Н = 1,0 м.
Решение:
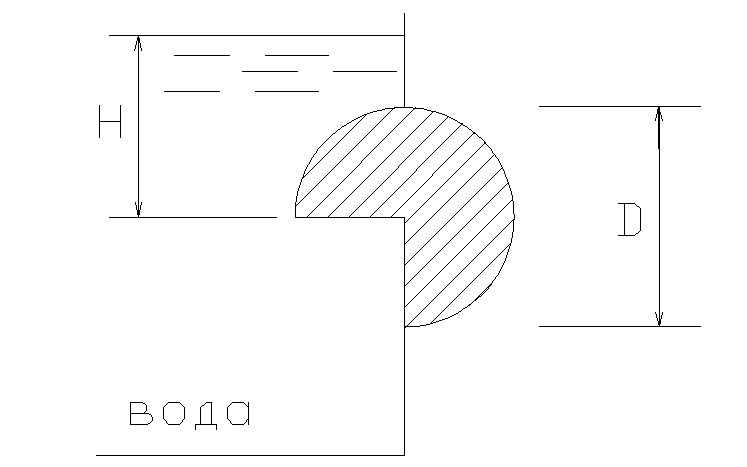 Так как затвор выполнен в виде цилиндра,
Так как затвор выполнен в виде цилиндра,
то для нахождения усилия на цапфы используем
расчетные формулы для определения сил
гидростатического давления на криволинейную поверхность:
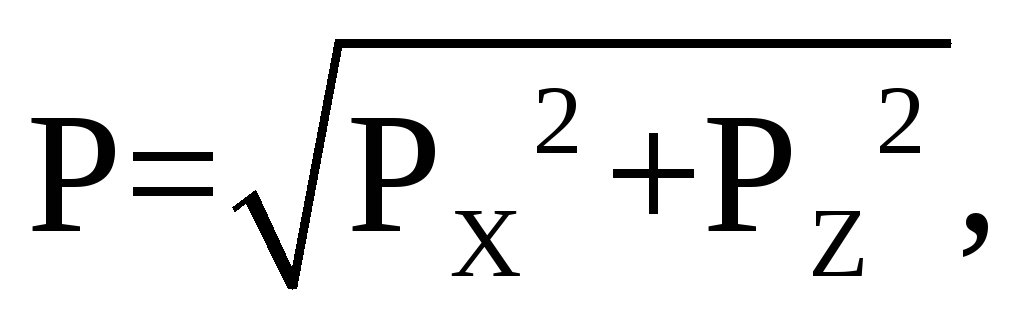
где Р х – горизонтальная составляющая силы гидростатического давления, определяется по формуле:
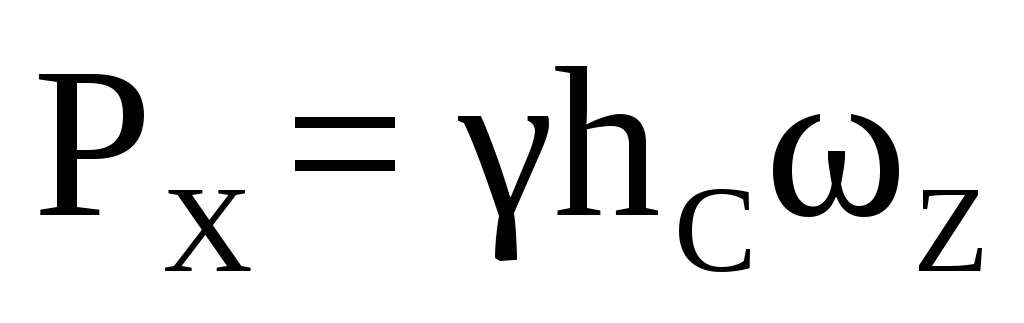 ,
,
где h C – заглубление центра тяжести вертикальной
проекции криволинейной поверхности
под уровень свободной поверхности (в
данном случае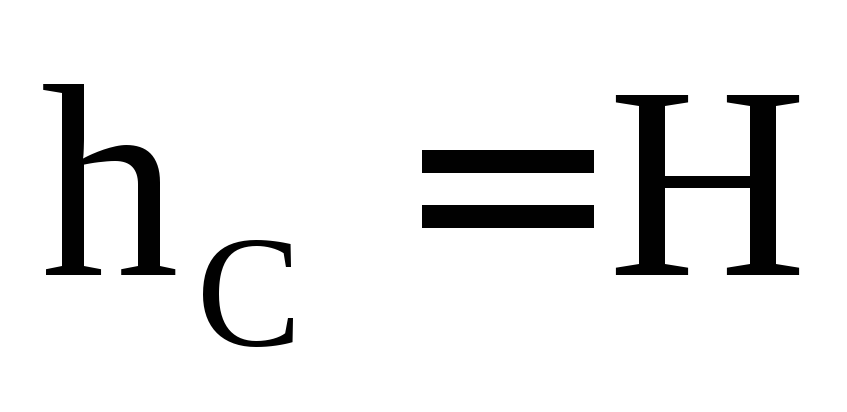 );
);
 −
площадь вертикальной проекции
криволинейной поверхности:
−
площадь вертикальной проекции
криволинейной поверхности:
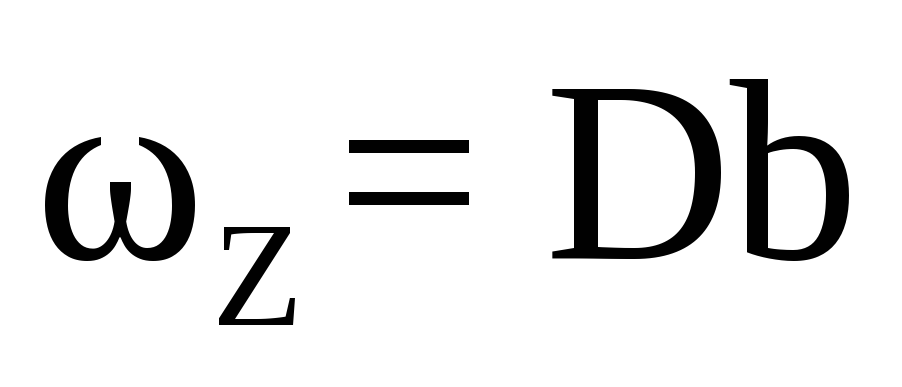 .
.
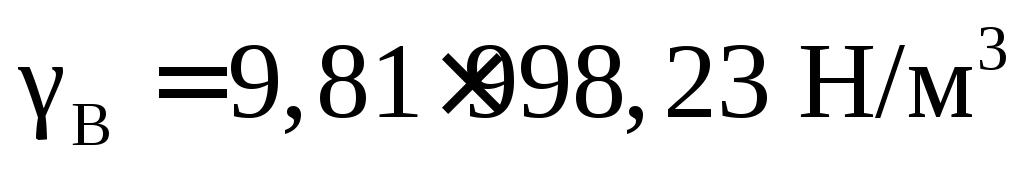 − удельный вес воды приt= 20ºС .
− удельный вес воды приt= 20ºС .
P Z – вертикальная составляющая силы гидростатического давления, которая равна весу жидкости в объеме тела давления (тело давления показано на расчетной схеме):
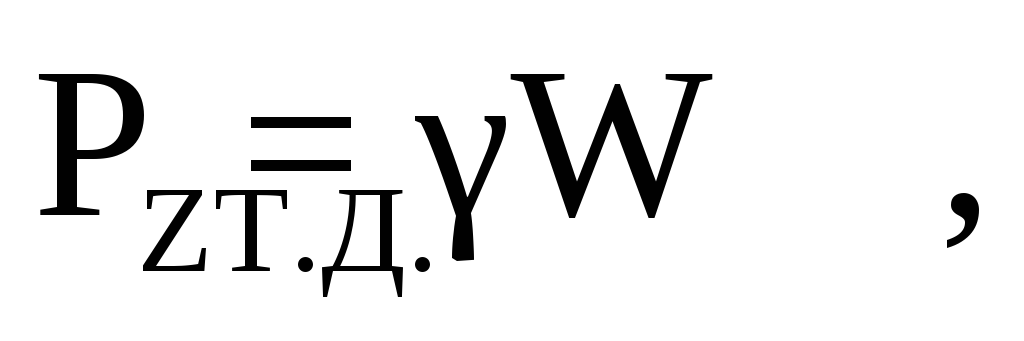
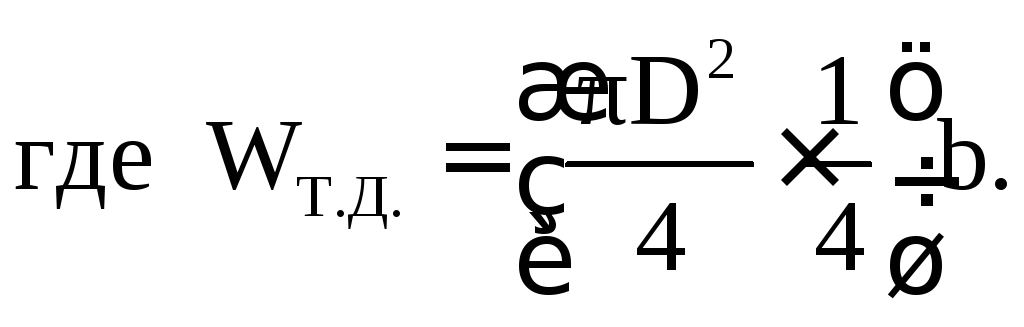
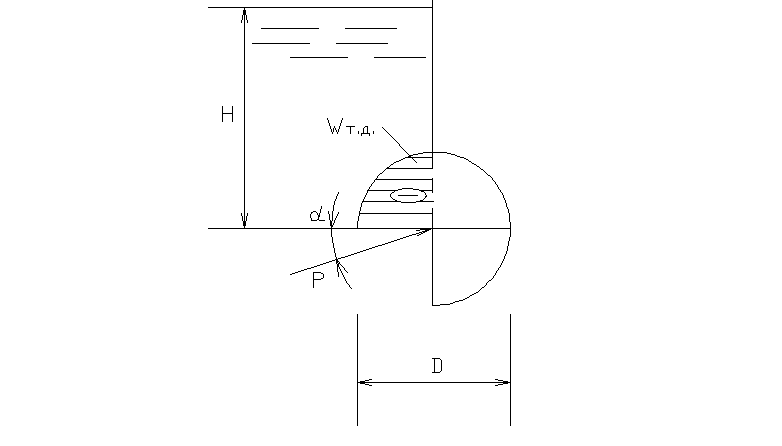
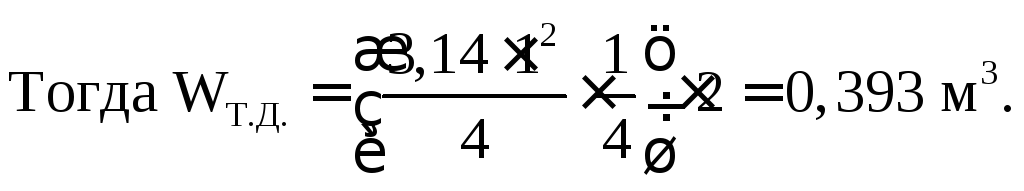
Полная сила гидростатического давления,
действующая на цапфы, расположенные на
горизонтальной оси цилиндра, равна:
Направление этой силы определяется тангенсом угла α:
Линия действия (приложения) силы Р проходит через центр цилиндра (через цапфы).
Найдем теперь момент от воздействия жидкости на затвор – М.
Этот момент в общем случае состоит
из
- момента от горизонтальной
составляющей силы
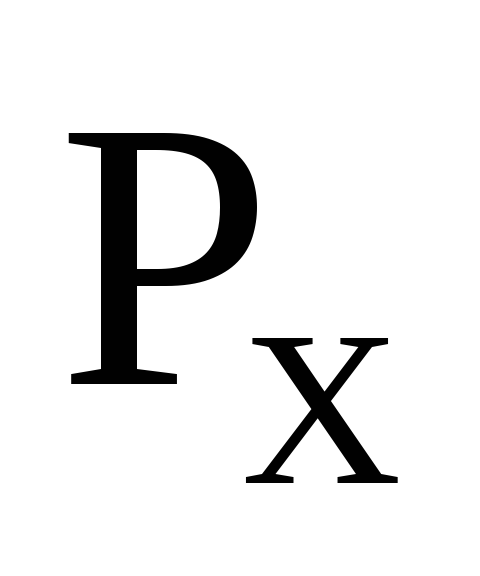 ;
-
момента от вертикальной составляющей
силы
;
-
момента от вертикальной составляющей
силы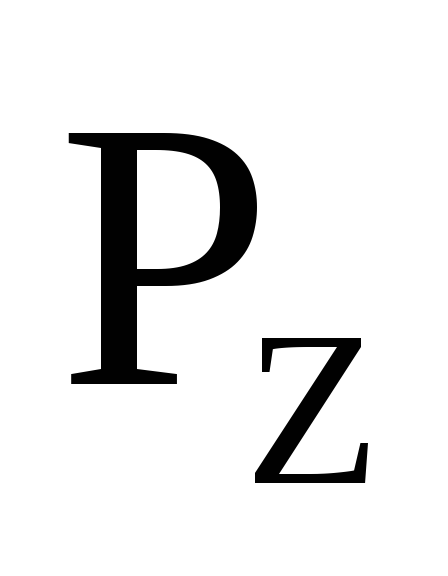 .
.
Момент от горизонтальной составляющей, в свою очередь, состоит из двух моментов: - от горизонтальной составляющей, действующей на верхнюю (криволинейную поверх- ность) - от горизонтальной составляющей, действующей на нижнюю часть цилиндра.
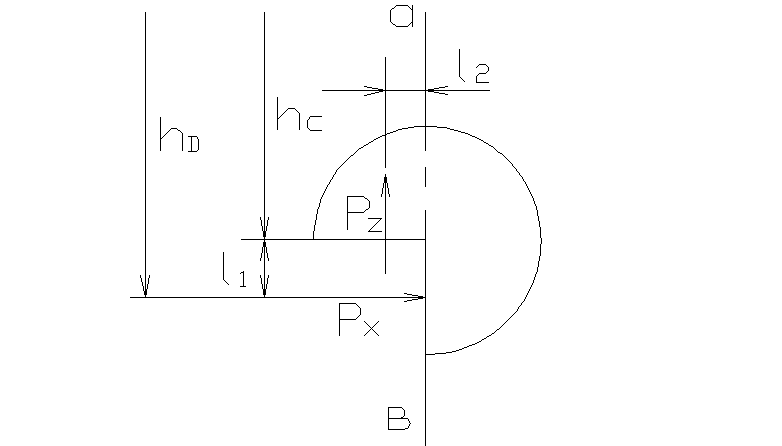
Однако эти две горизонтальные составляющие можно привести к одной со своим плечом действия:
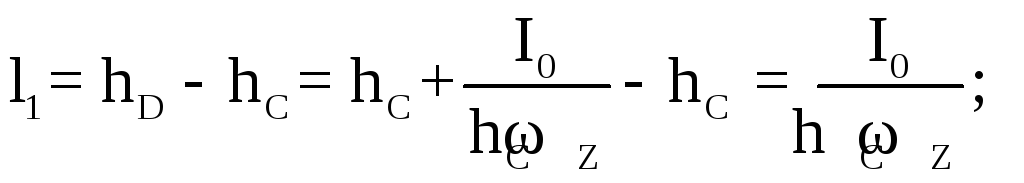
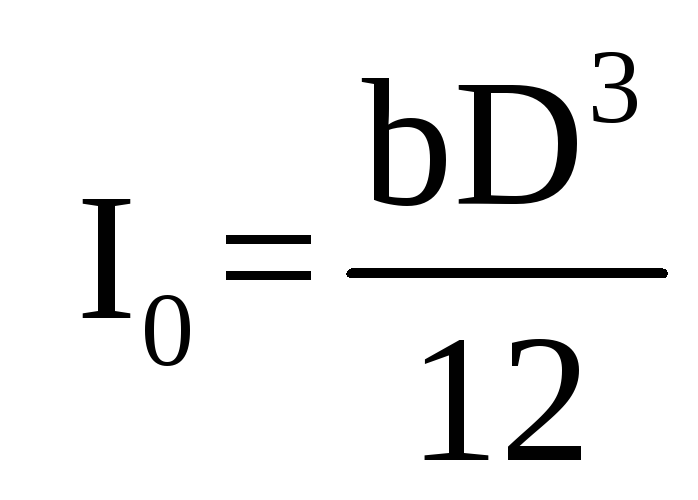 – момент инерции проекции
– момент инерции проекции ,
,
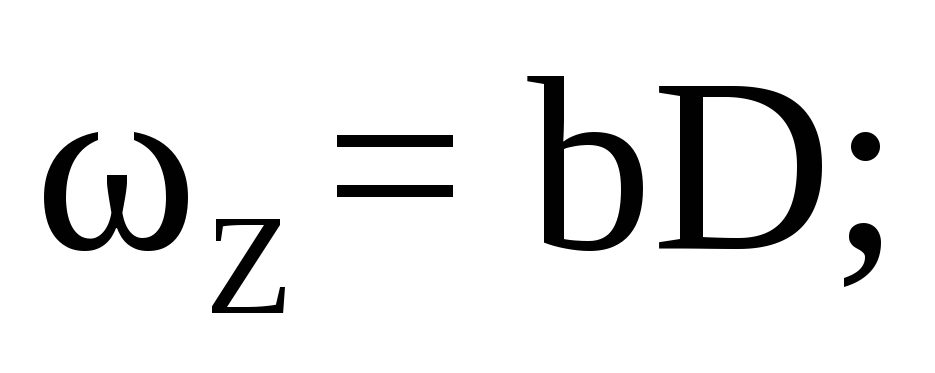
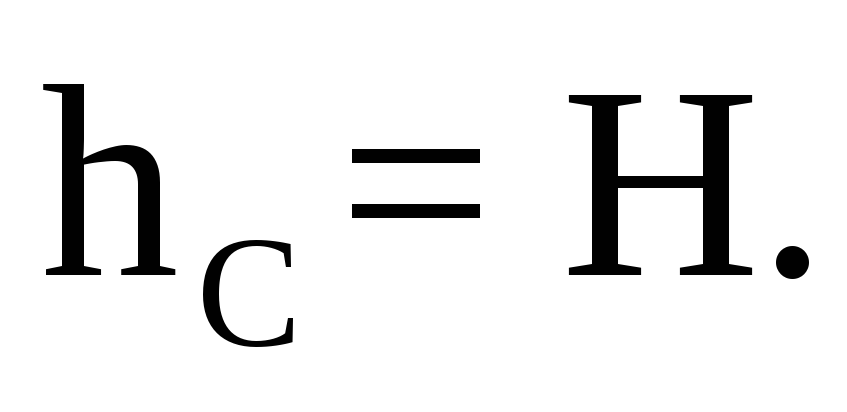
Таким образом, момент от горизонтальной составляющей будет:
Момент от вертикальной составляющей
будет определяться силой
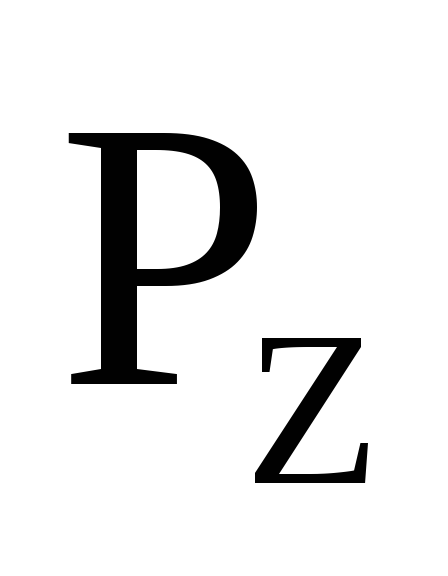 и плечом
и плечом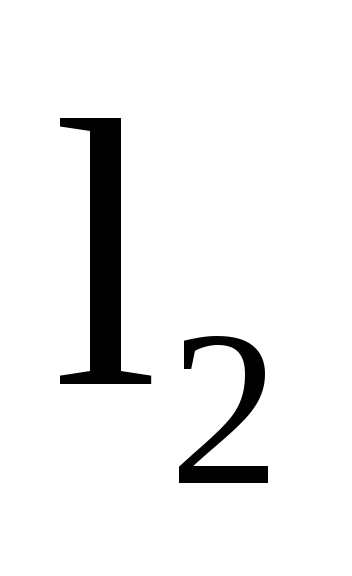 .
.
Сила
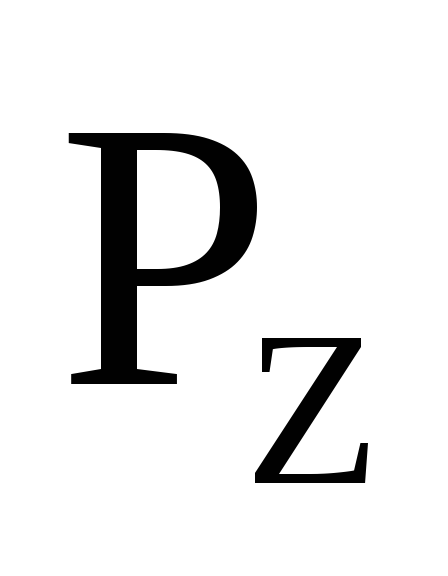 будет
равна выталкивающей силе (архимедовой)
численно равной весу жидкости (воды) в
объеме, вытесненной 1/4 объема цилиндра:
будет
равна выталкивающей силе (архимедовой)
численно равной весу жидкости (воды) в
объеме, вытесненной 1/4 объема цилиндра:
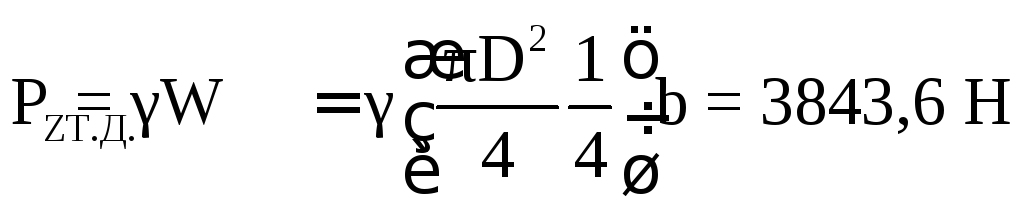 .
.
Составляющая
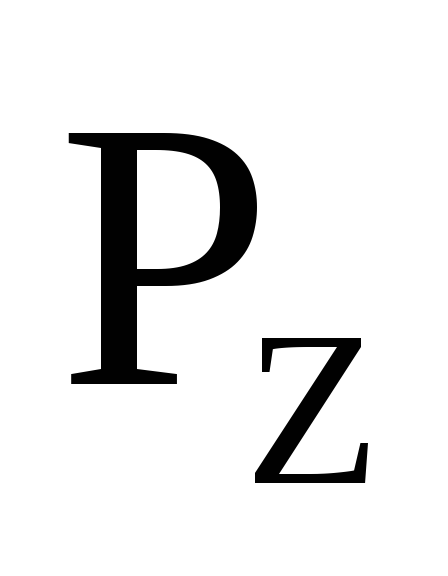 проходит на расстоянии
проходит на расстоянии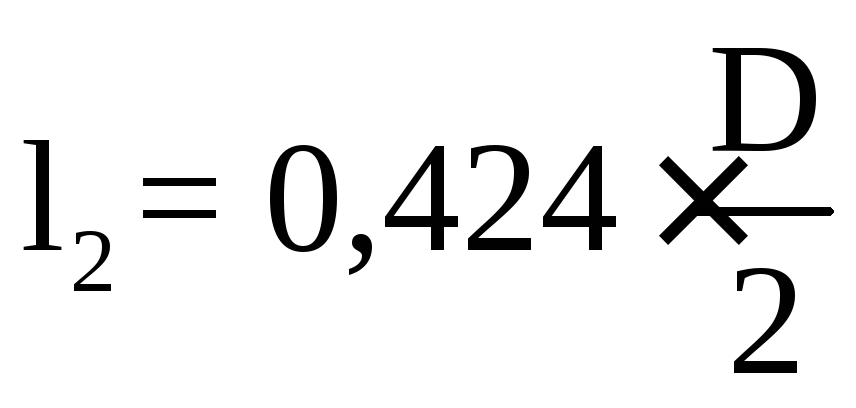 от линииab(см. расчетную
схему).
от линииab(см. расчетную
схему).
Тогда момент от
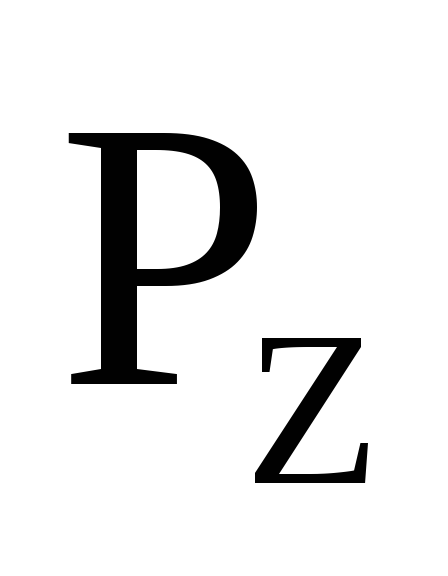 равен:
равен:
(вращает по часовой стрелки).
Суммарный момент от воздействия жидкости на затвор составит:
(вращает против часовой стрелки).
Ответ: .
2.45
. В шарообразном углублении радиуса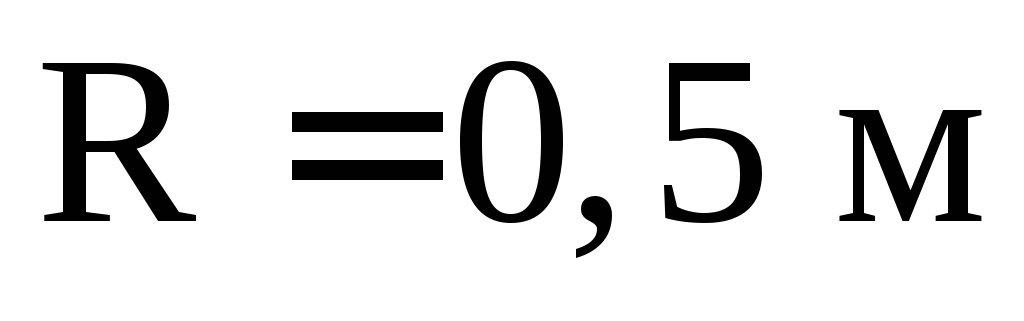 налита вода весом
налита вода весом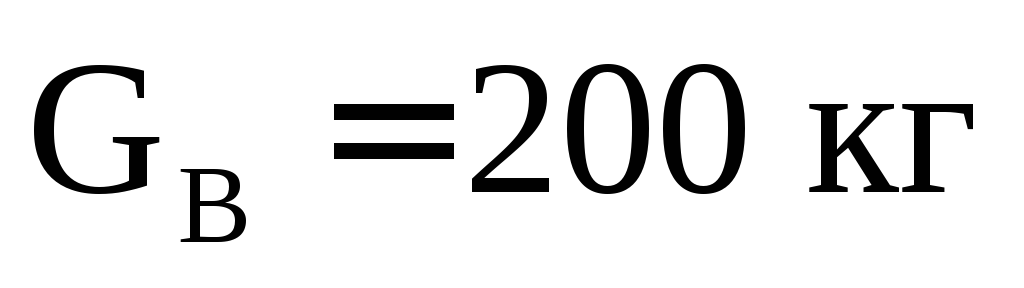 .
В воду погружен шарик радиусом
.
В воду погружен шарик радиусом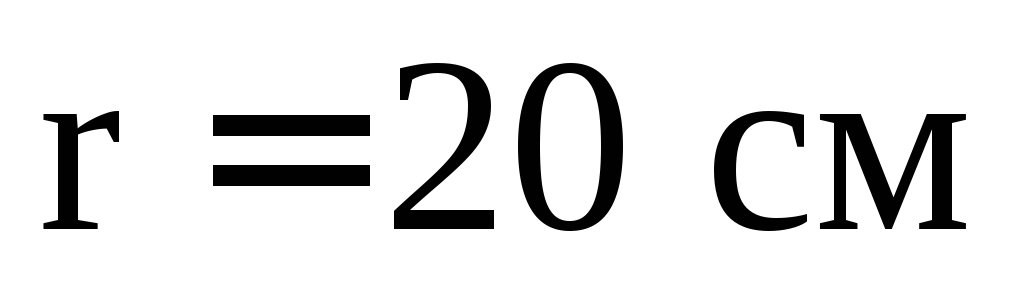 .
Каким должен быть вес шарика
.
Каким должен быть вес шарика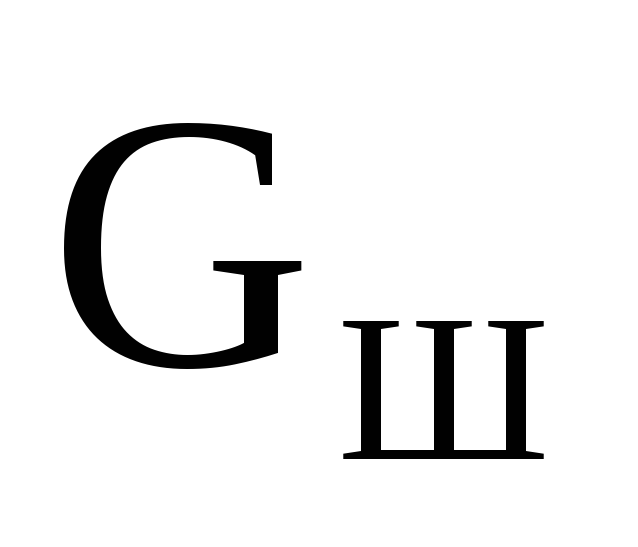 ,
чтобы он плавал в положении, концентричном
углублению?
,
чтобы он плавал в положении, концентричном
углублению?
Решение:
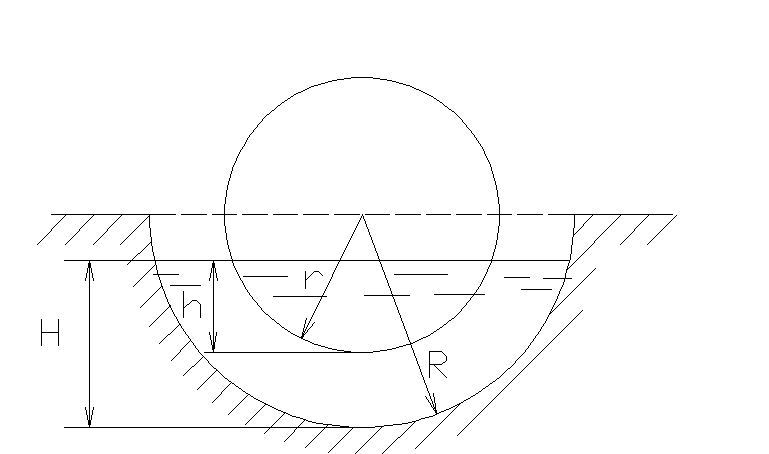
Составим равенство объемов:
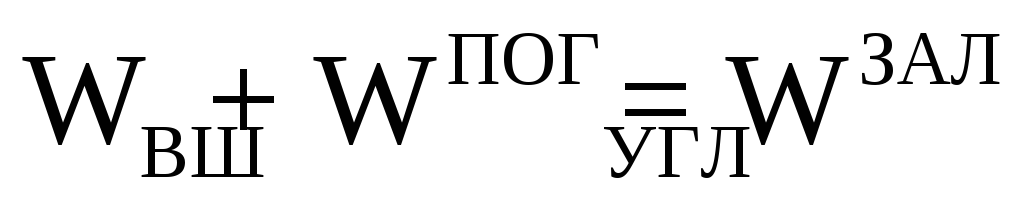 ,
,
где
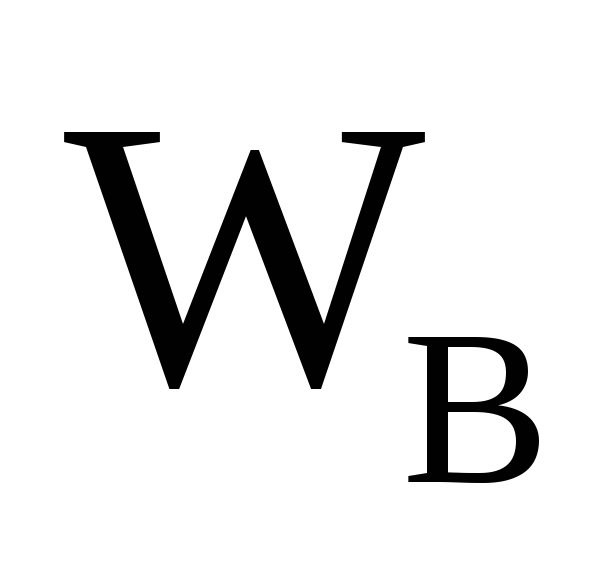 – объем воды в углублении;
– объем воды в углублении;
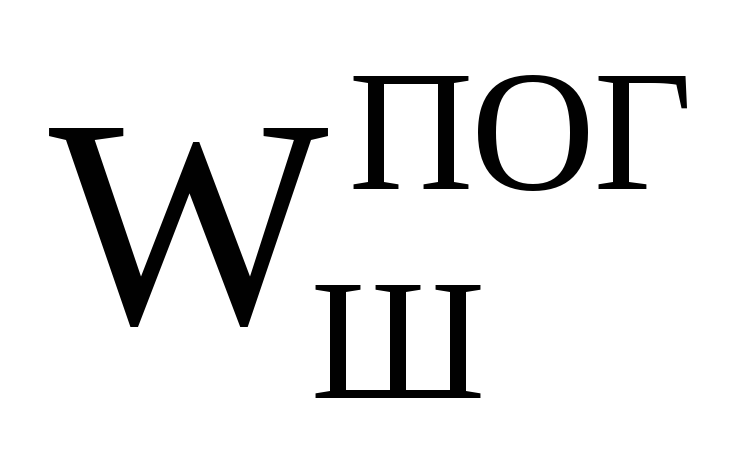 – объем погруженной части
– объем погруженной части
шарика в воду;
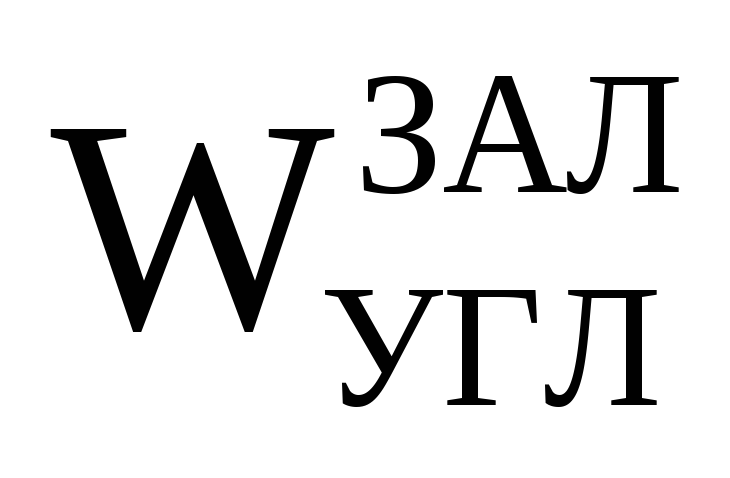 – суммарный объем воды и погруженной
части шарика.
– суммарный объем воды и погруженной
части шарика.
Тогда
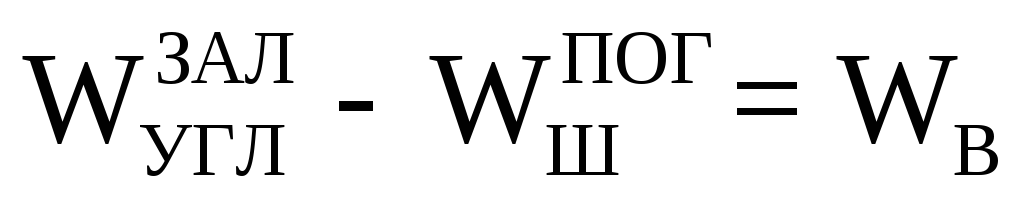 или
или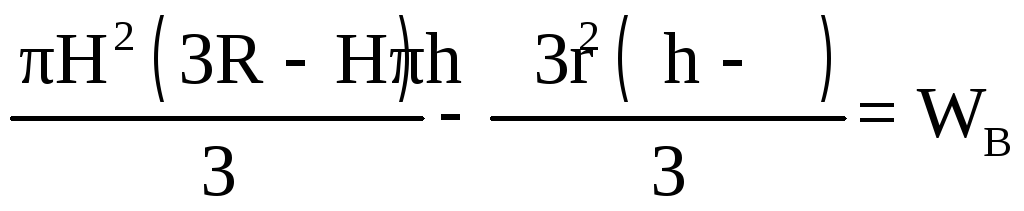 .
.
Из рисунка следует, что
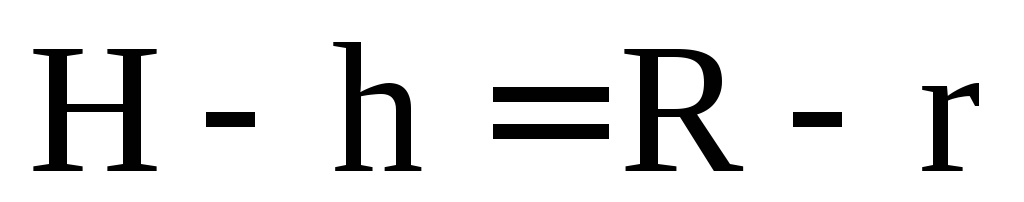 или
или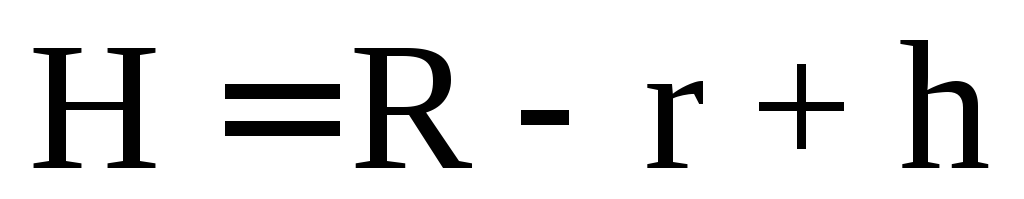 .
.
Обозначим
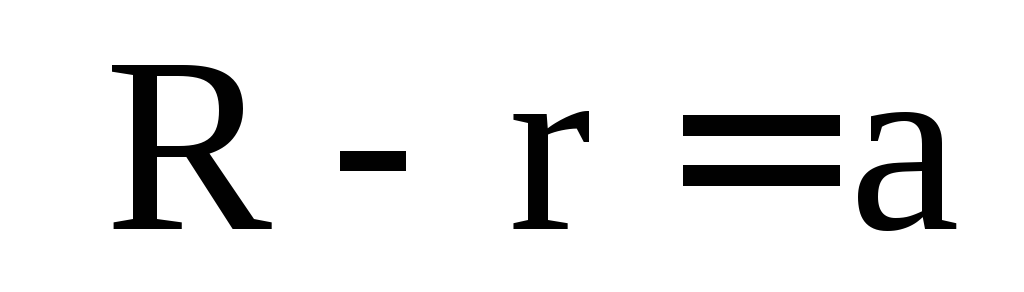 .
Тогда уравнение примет вид:
.
Тогда уравнение примет вид:
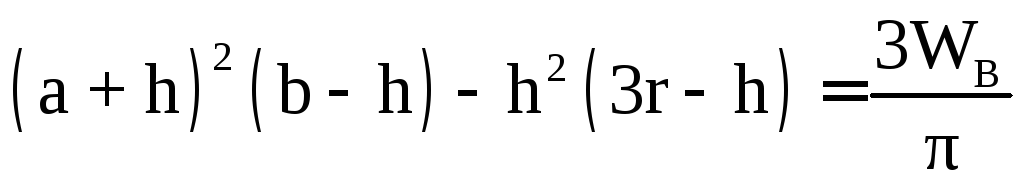 ,
где
,
где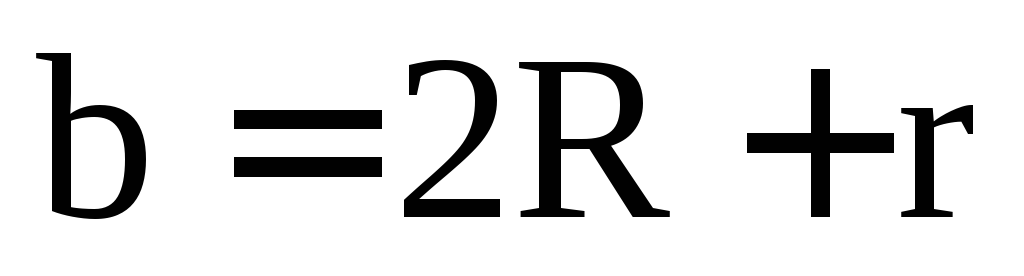 .
.
Вычислим значения:
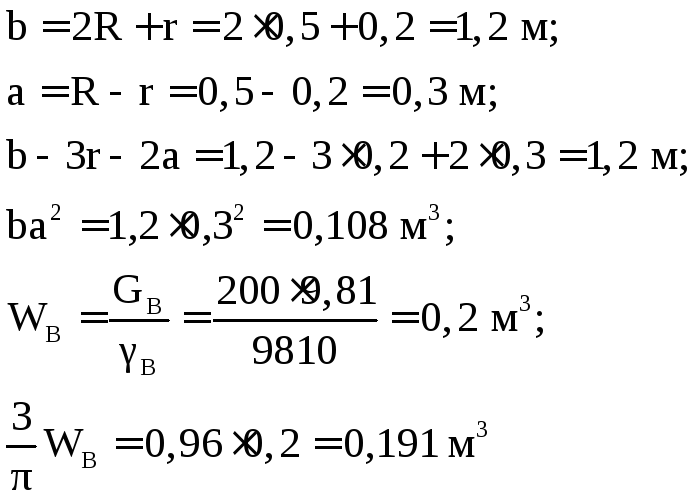
подставим в предыдущее уравнение и запишем его относительно h:
Решение этого квадратного уравнения будет h= 0,109 м.
Так как
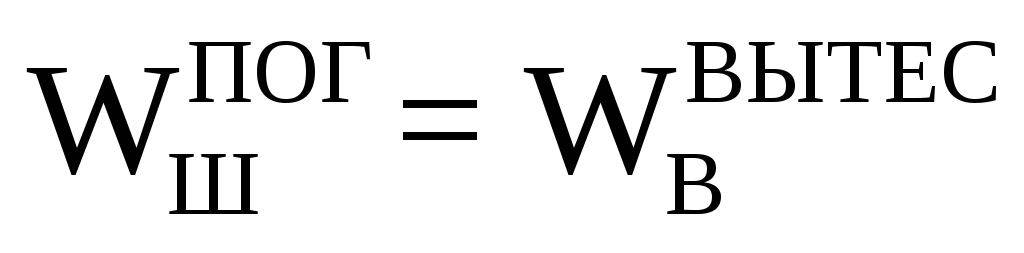 ,
то вес шарика
,
то вес шарика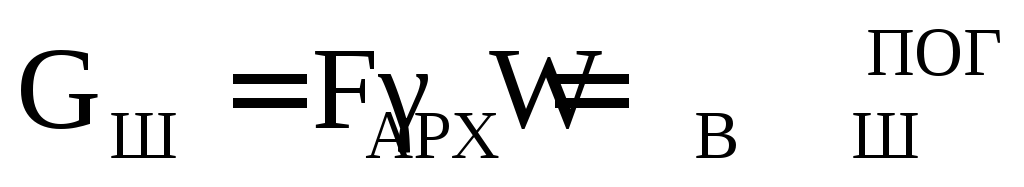 или
или
Ответ:
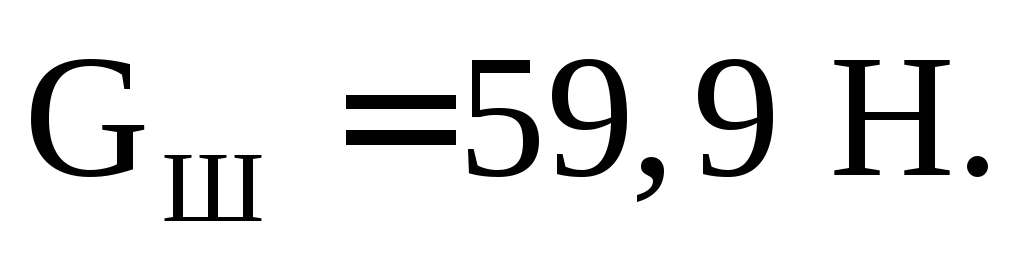
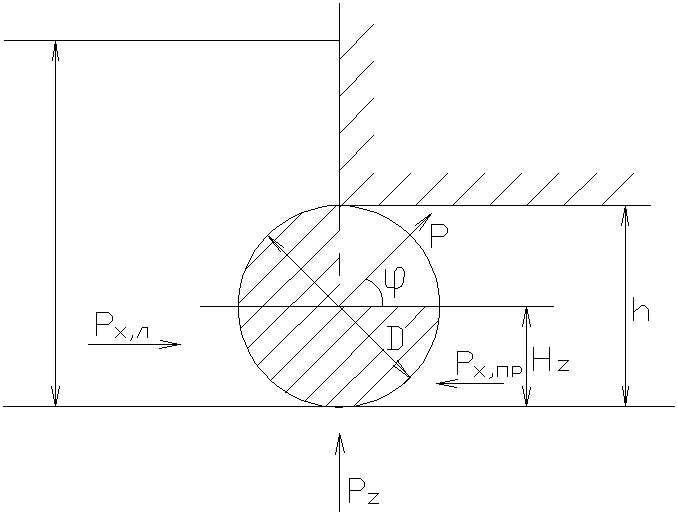
2.46. Определить величину и направление равнодействующей силы давления воды на цилиндрический затвор плотины, перекрывающий донное отверстие высотойh=D=1,2 м.и ширинойb= 6 м. Глубина воды слева Н 1 = 3,8 м, справа Н 2 =D/2.
Решение: Равнодействующая сила давления воды на цилиндрический затвор определяется так:
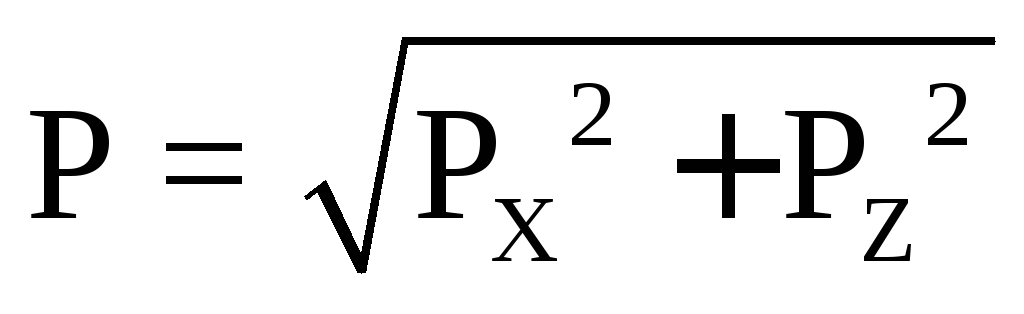 ,
,
где P X  горизонтальная составляющая силы
давления воды;
горизонтальная составляющая силы
давления воды;
P Z – вертикальная составляющая силы давления воды.
Найдем горизонтальную составляющую P X . Она складывается из силы давления воды, действующей слеваP X л и справаP X пр:
P X л = р С.л ω z л
= γ(Н 1 +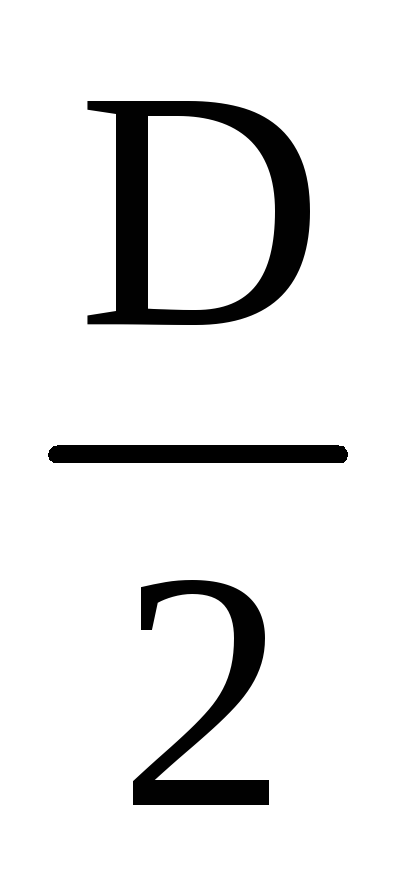 )Db.
)Db.
Аналогично:
P X пр = р с.пр ω z
пр = γ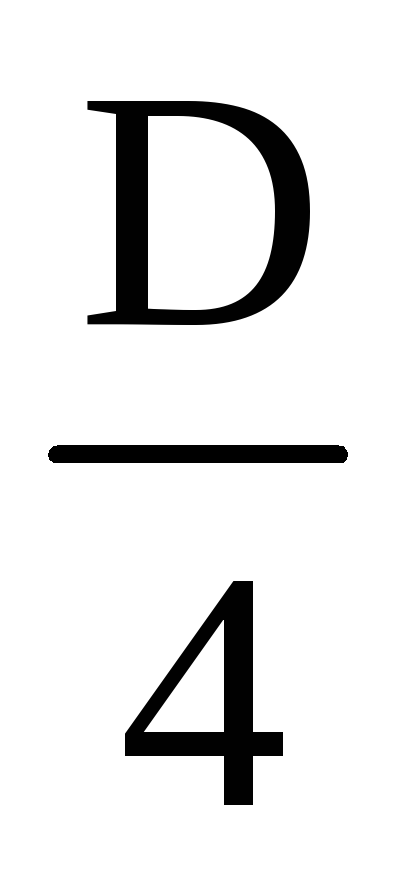
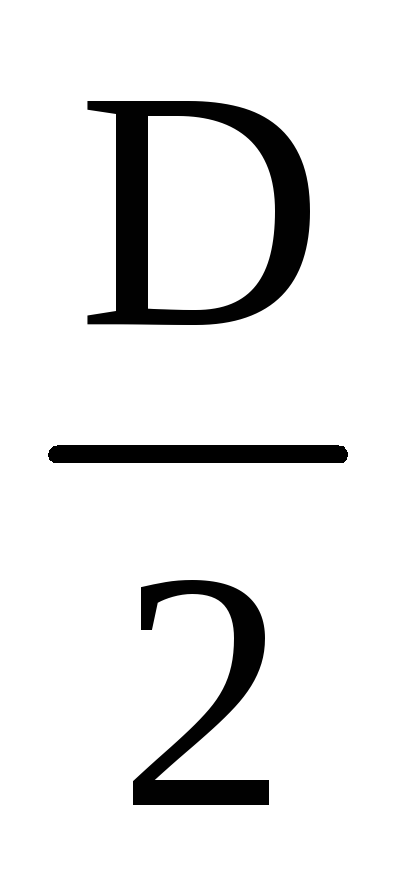 b.
b.
Тогда равнодействующая горизонтальных сил составит:
P X
=P X л -P X пр
= γ(Н 1 +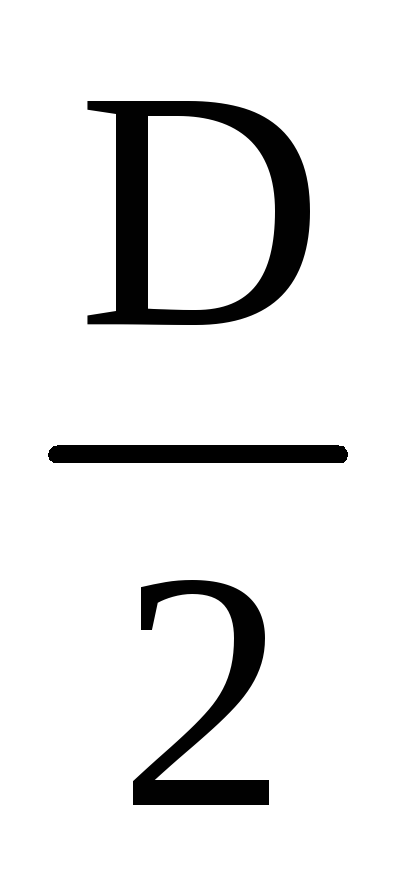 )Db– γ
)Db– γ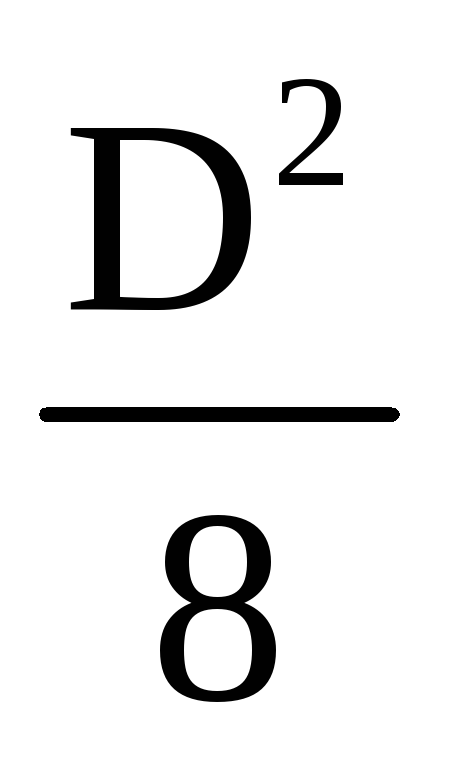 b= γb[(H 1 −
b= γb[(H 1 −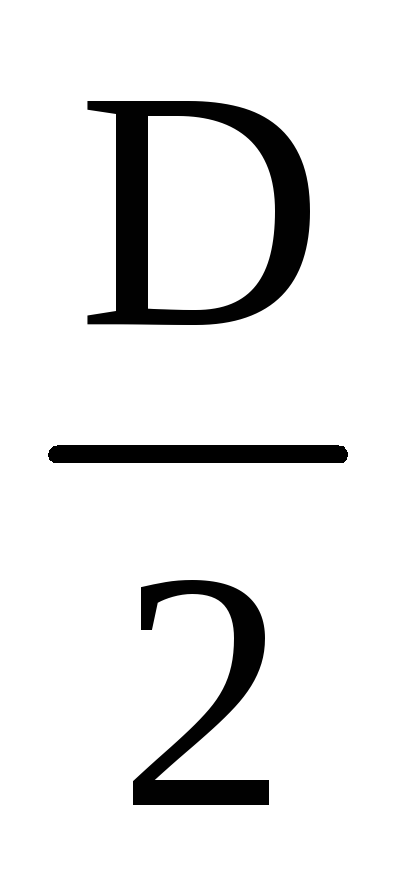 )D−
)D−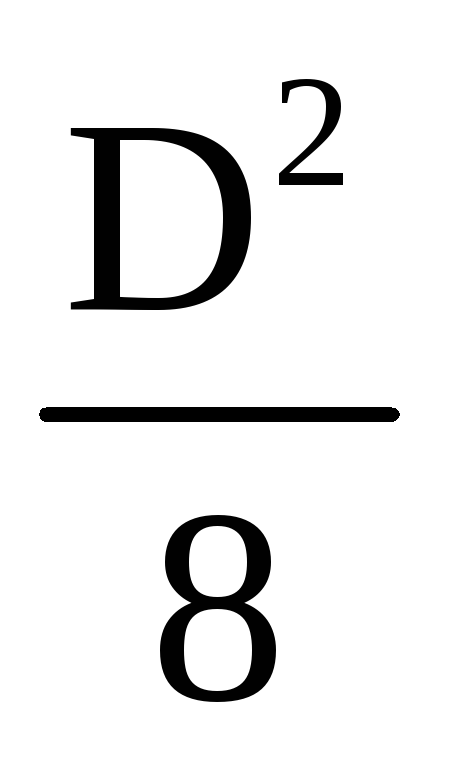 ];
];
P X
= 998 ∙ 9,81 ∙ 6 ∙ [(3,8 −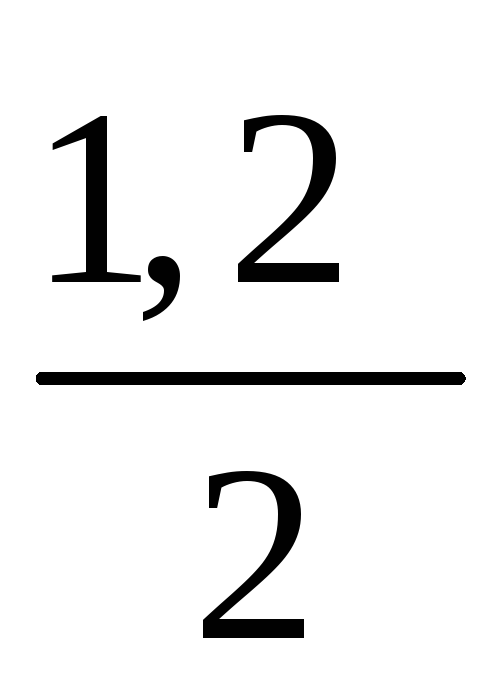 )
∙ 1,2 −
)
∙ 1,2 −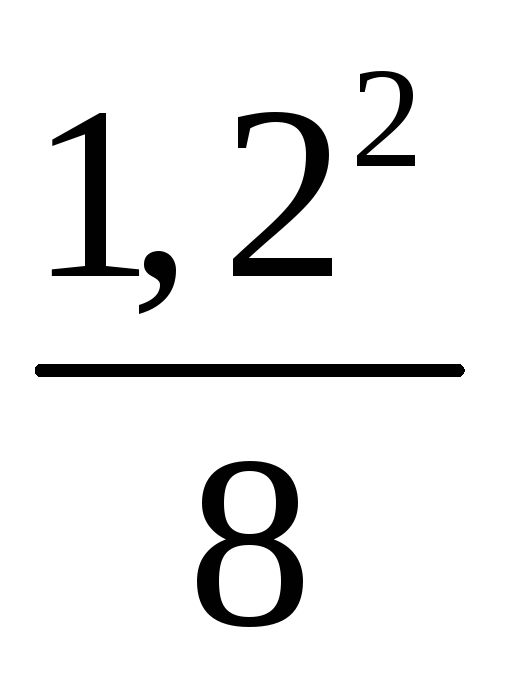 ]
= 215 кН.
]
= 215 кН.
Найдем вертикальную составляющую P Z . Она равна весу жидкости в объеме тела давления (на рисунке заштриховано):
P Z
= γW= γ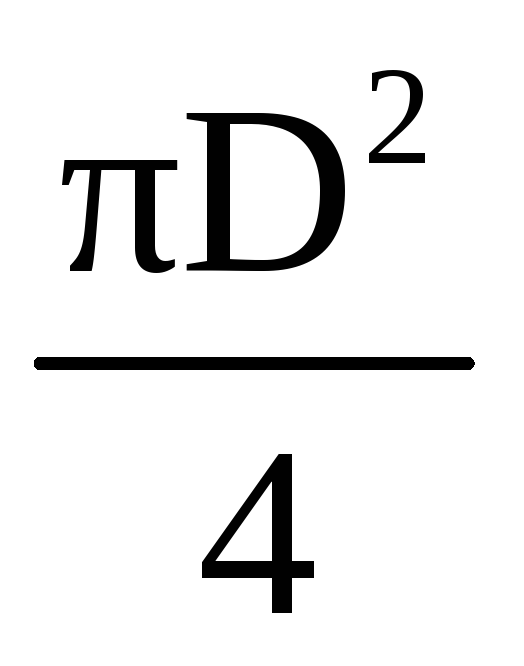 b=γb(3/16)πD 2 ;
b=γb(3/16)πD 2 ;
P Z = 998 ∙ 9,81 ∙ 6 ∙ (3/16) ∙ 3,14 ∙ 1,2 2 = 49,8 кН.
Суммарная сила давления:
Угол наклона силы Pк горизонту:
γ=arctg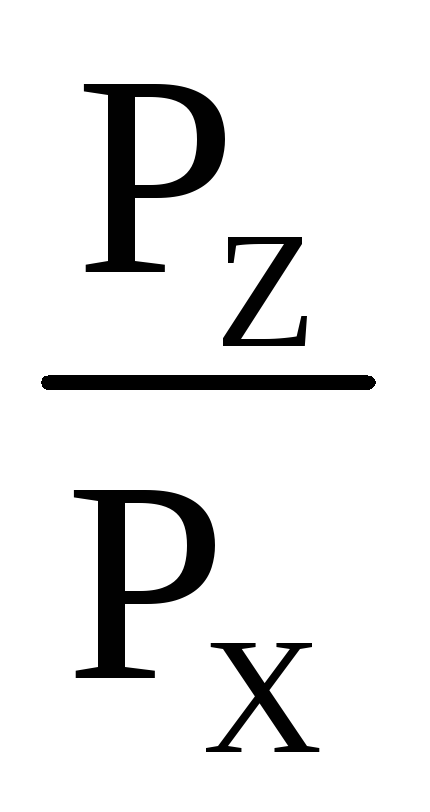 =arctg
=arctg
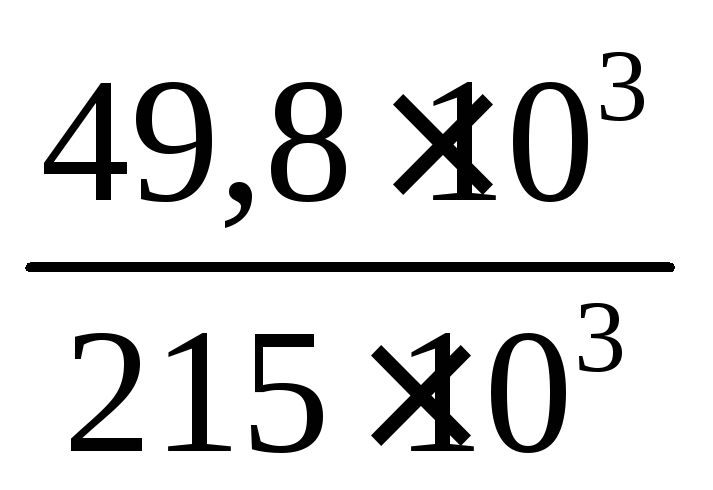 =13º5".
=13º5".
Ответ: P= 220,7 кН; γ = 13º5".
2.47. Стальной шарик радиусомR= 7 см закрывает отверстие диаметромD= 10 см в плоской стенке, удерживаясь силой гидростатического давления. Определить, при каком напоре водыhшарик оторвется от отверстия.
Решение:
Н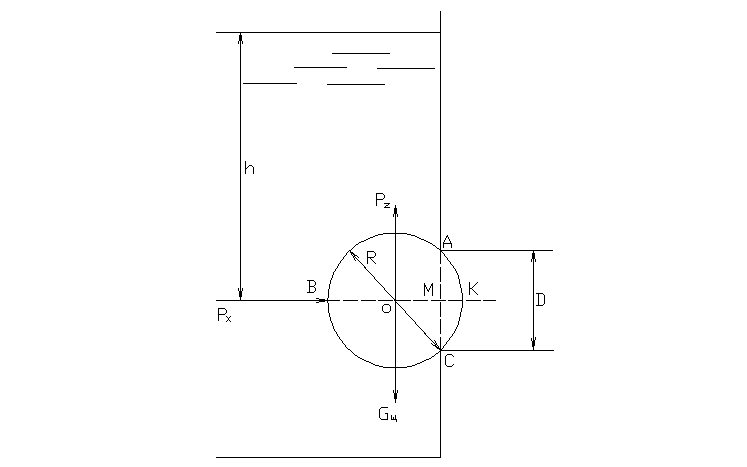 айдём
вес шарика:
айдём
вес шарика: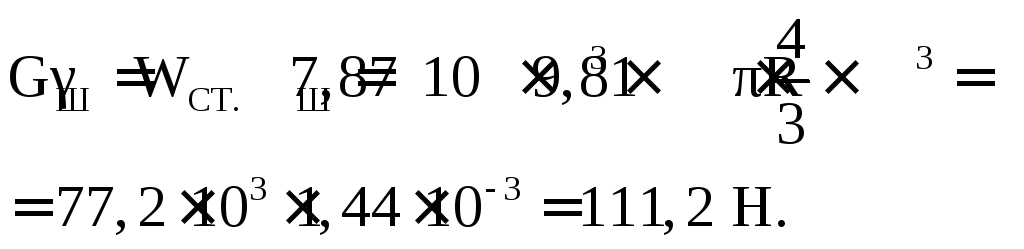 Вертикальная составляющая силы
гидростатического давления воды на
шарик:
Вертикальная составляющая силы
гидростатического давления воды на
шарик:
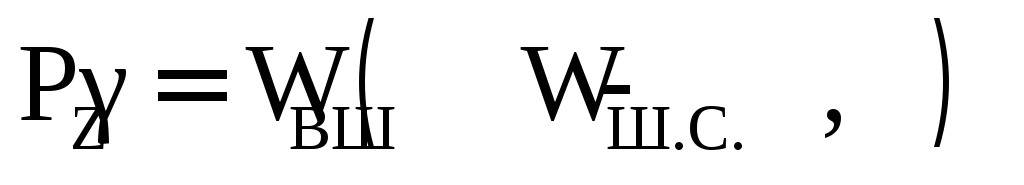
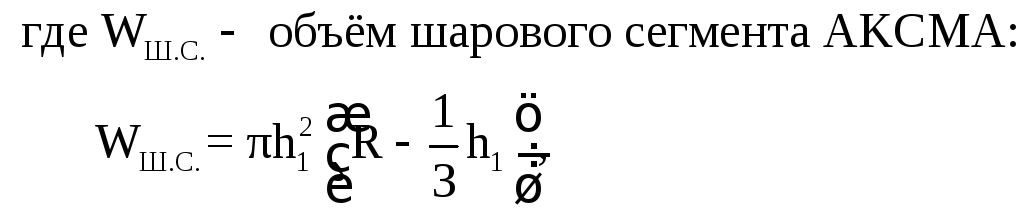
Вес шарика в воде будет на величину
 меньше,
т.е.
меньше,
т.е.
Для сохранения равновесия необходимо составить уравнение моментов сил относительно точки C:
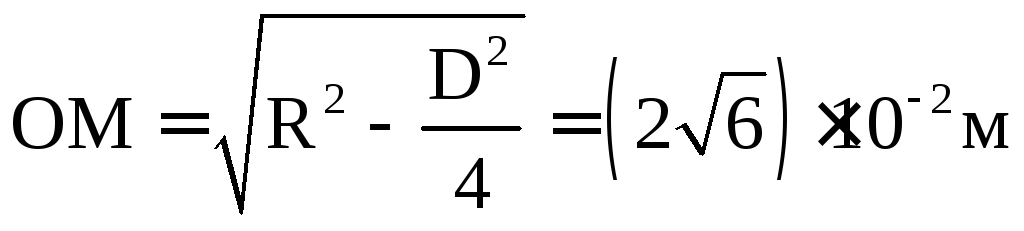 ,
,
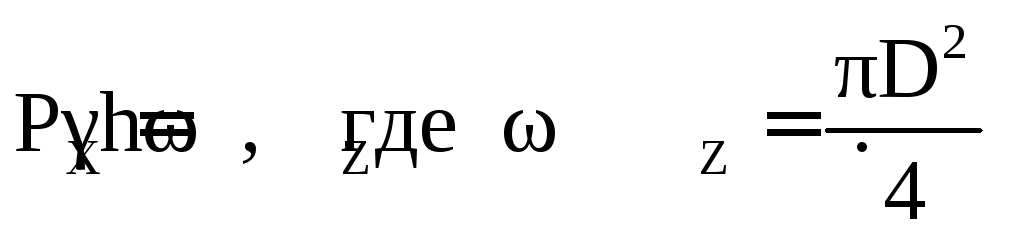
Тогда
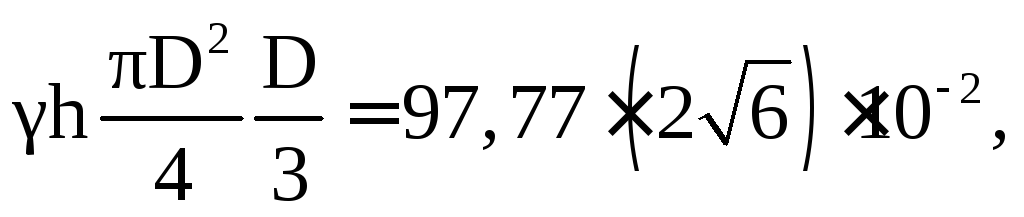
откуда найдём
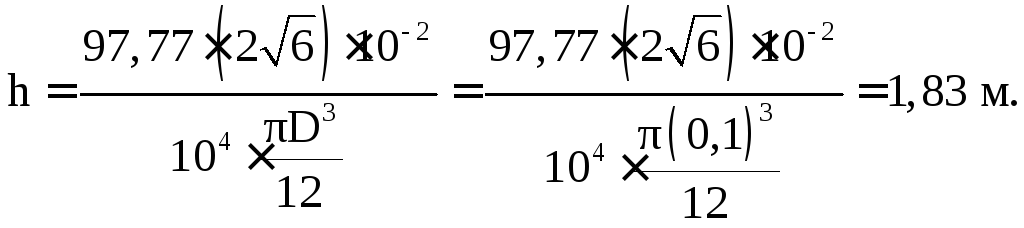
Ответ:
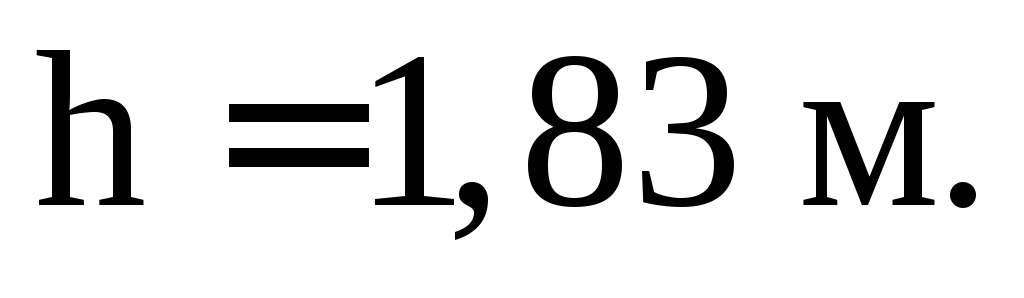
2.48.
Определить величину и направление
действия силы на сегментный затвор
ширинойb 3,0м,
радиусомR
3,0м,
радиусомR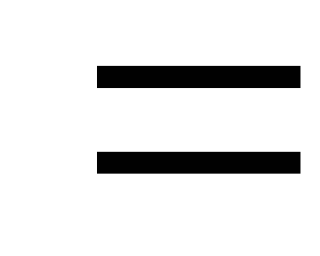 2,0м,
если известны углы
2,0м,
если известны углы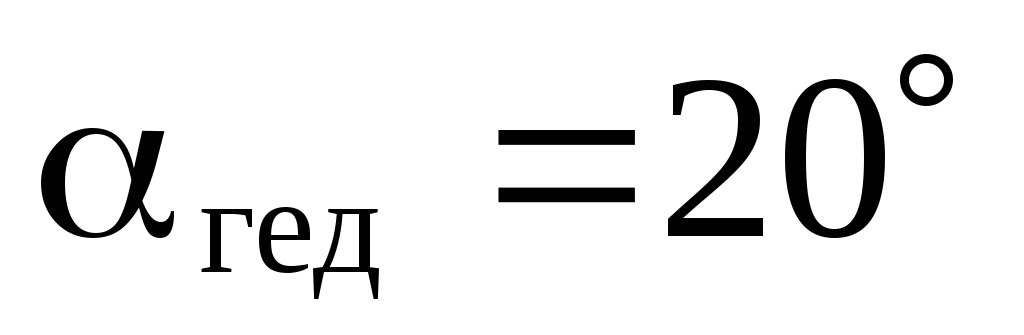 ,
,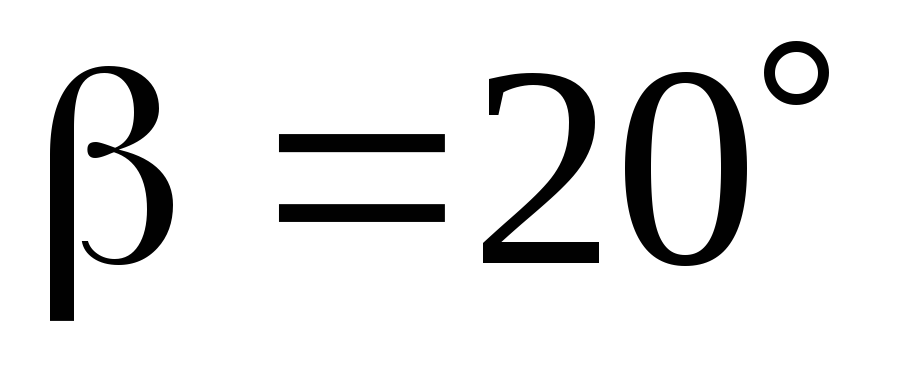 ,
,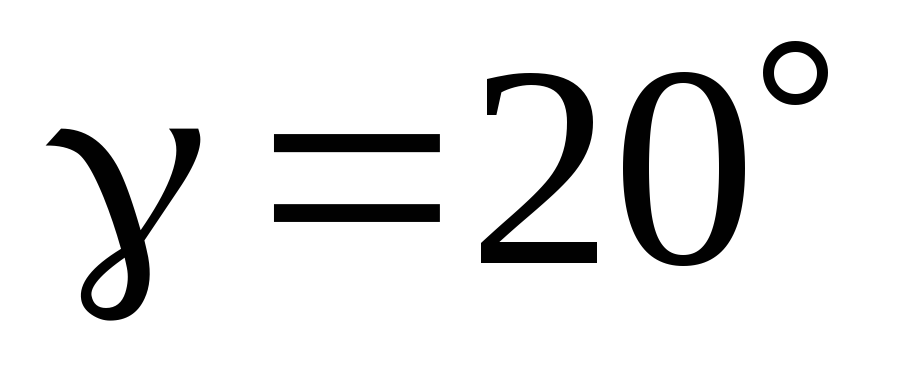 .
.
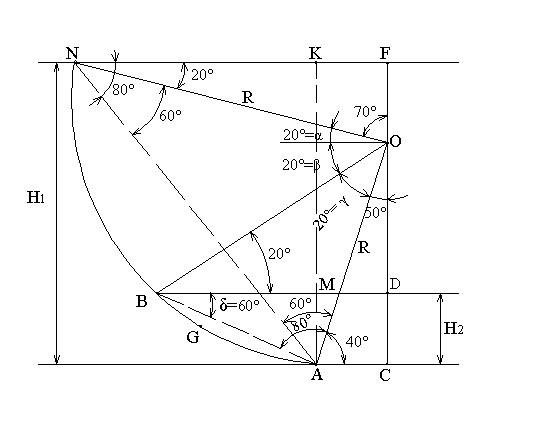
Решение:
Сила давления жидкости на сегментный затвор равна:
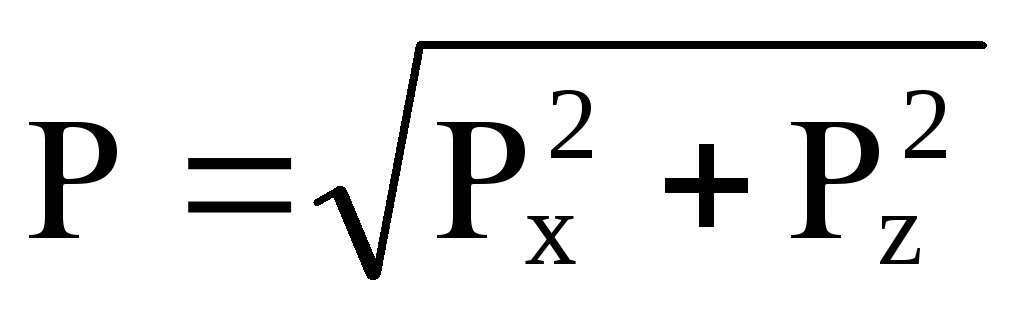 ,
,
а её направление определяется углом
 :
:
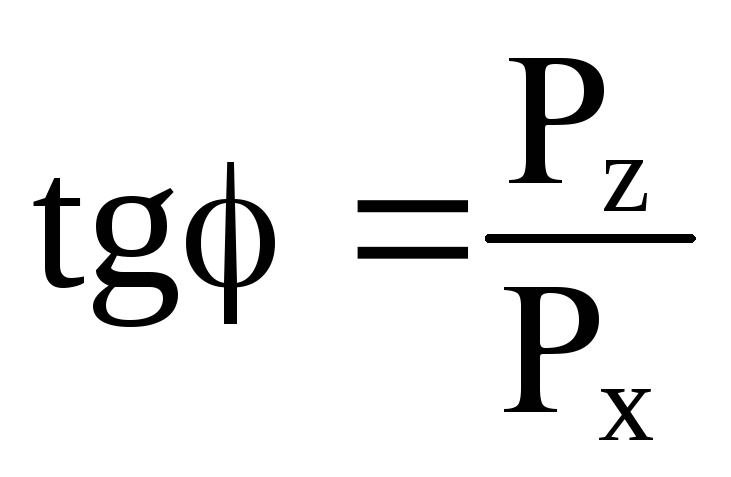 ,
,
где
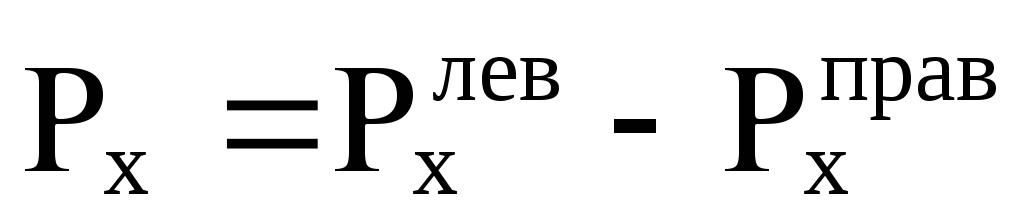 ;
;
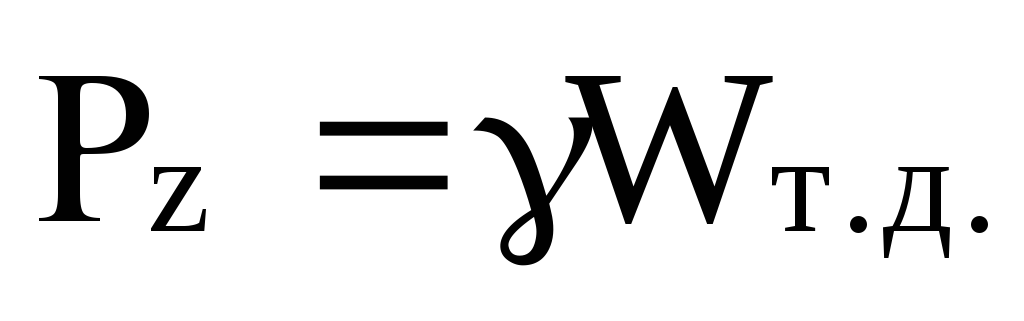 ,
,
где
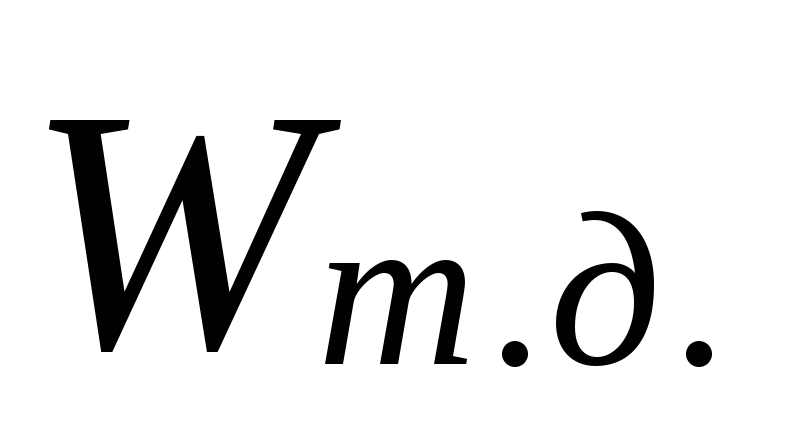 - объём тела давления, равный величине
- объём тела давления, равный величине
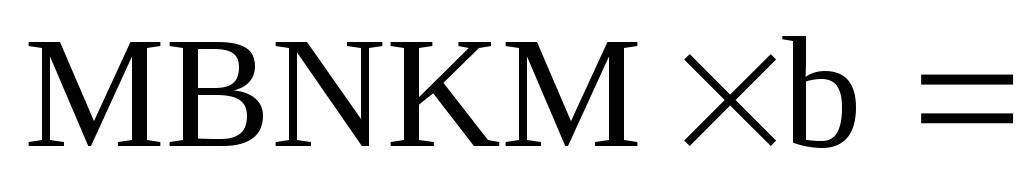
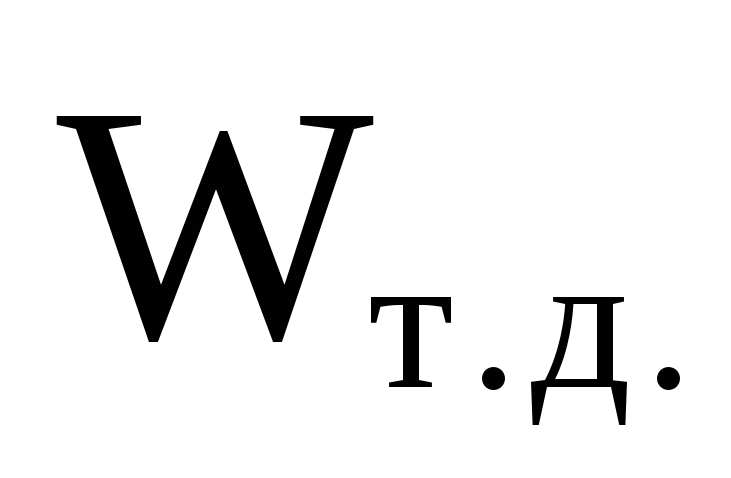
Найдём эти величины из геометрии:
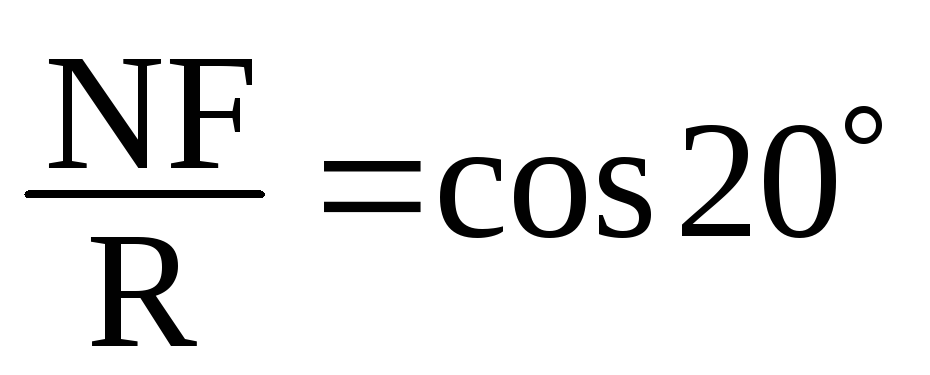 ;;
;;
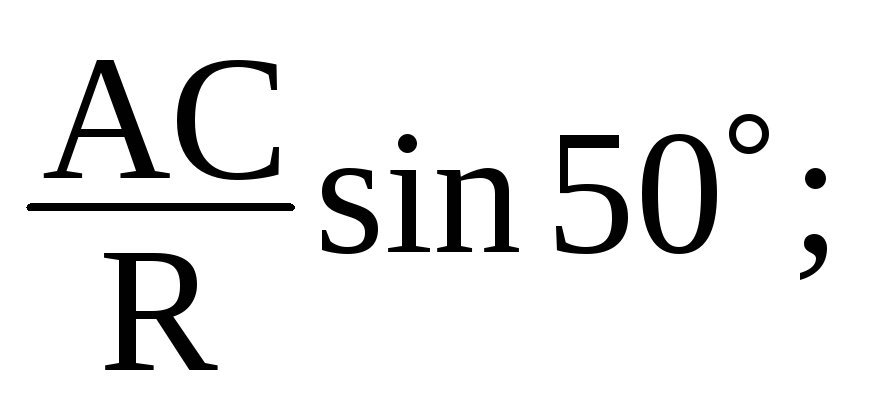 ;
;
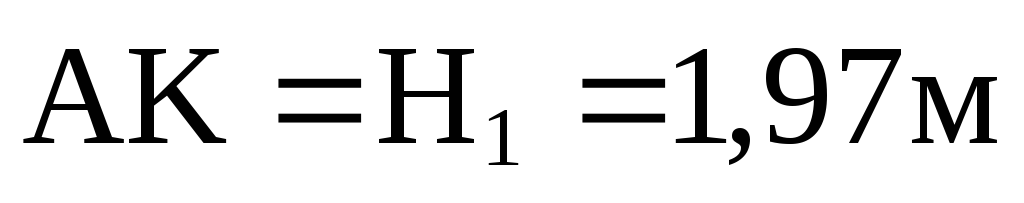 ;
;
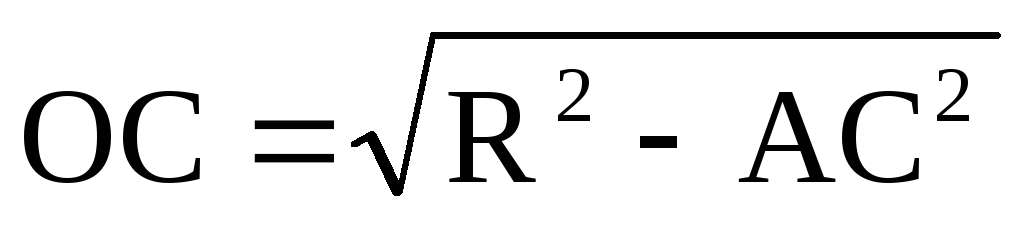 =
=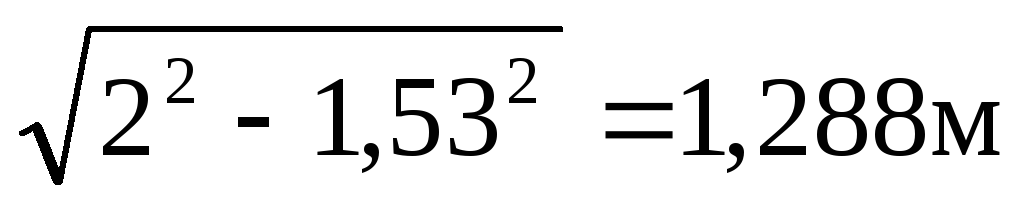 ;
;
![]() ;;
;;
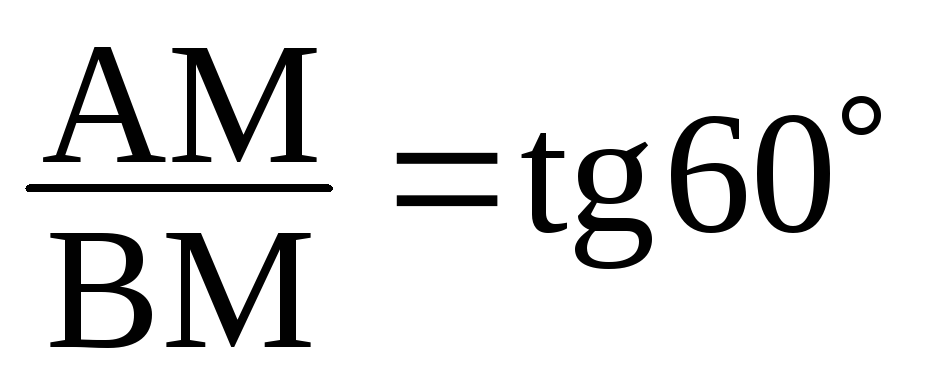 ;
;
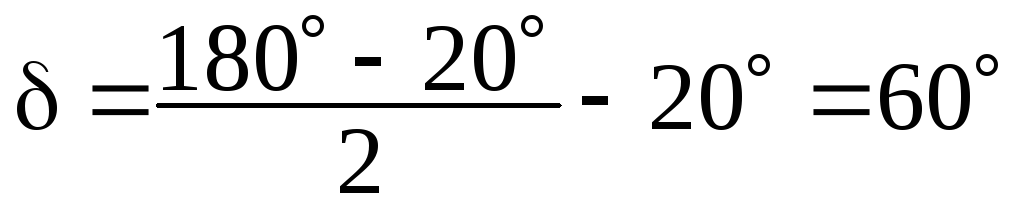 ,
,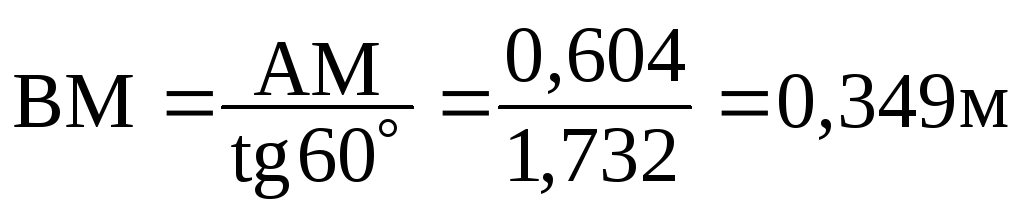 ;
;
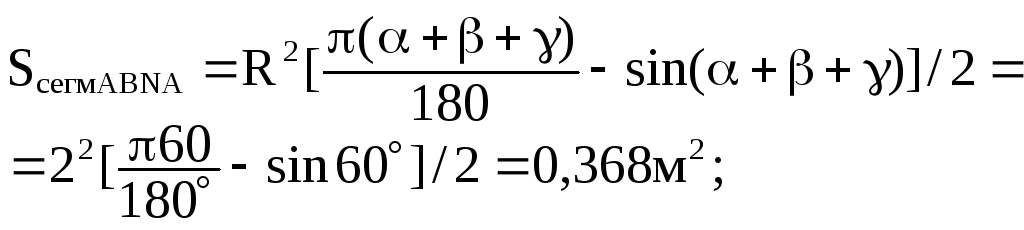
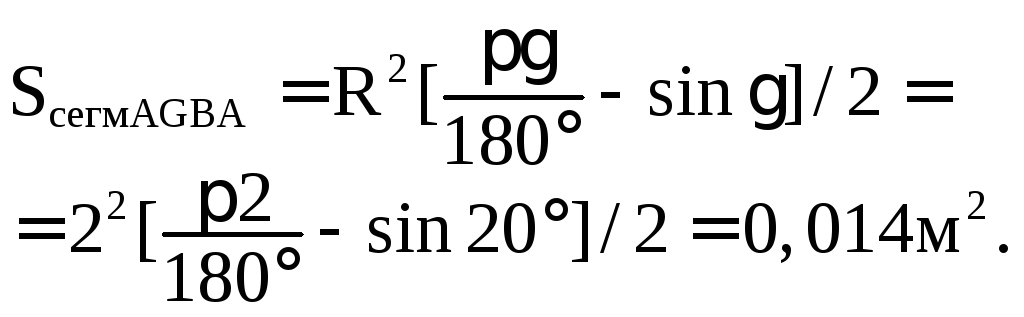
Тогда объём тела давления равняется
Найдём составляющие полной силы гидростатического давления. Горизонтальная, действующая слева, горизонтальная, действующая справа
Их сумма равна H.
Вертикальна составляющаяH.
Полная сила гидростатического давления на затвор составит
t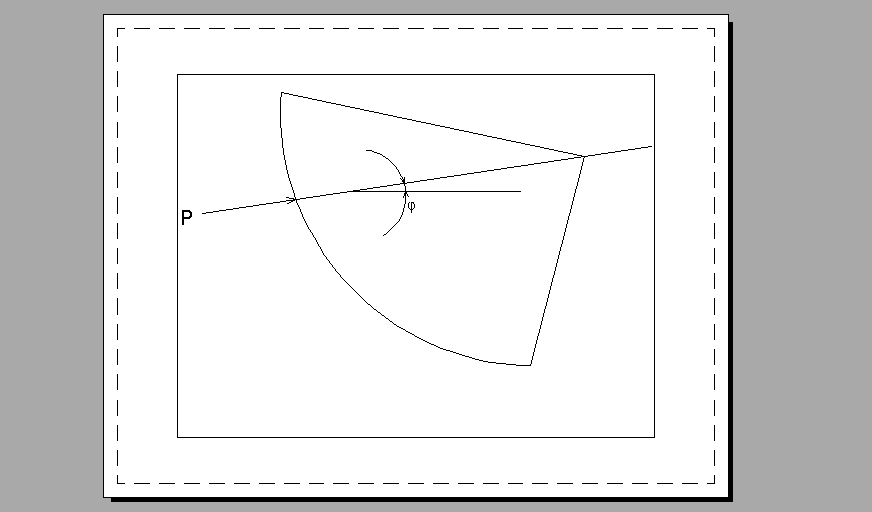 g
g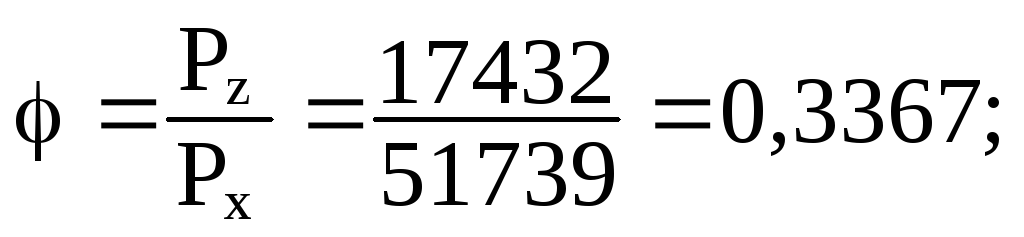 откуда
откуда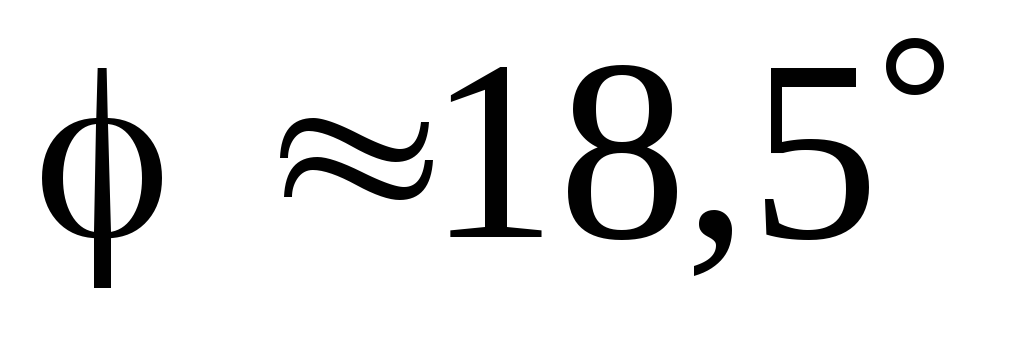 .
.
Ответ:
Р=54,6кН;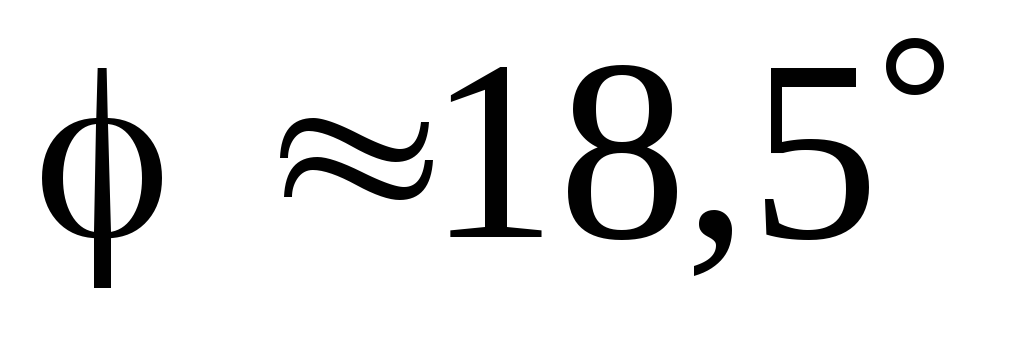 .
.
(06) Эпюры гидростатического давления.
Сила гидростатического давления жидкости на плоские стенки.
Центр давления.
Сила гидростатического давления жидкости на криволинейные стенки.
Закон Архимеда.
Котельная формула
Эпюры гидростатического давления
Эпюра гидростатического давления – графическое изображение закона распределения нормального гидростатического напряжения по поверхности. Давление можно рассматривать абсолютное, избыточное и весовое (только за счет жидкости). Если давление на поверхности жидкости совпадает с атмосферным давлением, то избыточное и весовое давления совпадают. Эпюры могут быть построены для всех перечисленных давлений, однако на практике строят обычно эпюры избыточного давления, принимая во внимание, что с другой стороны стенки также действует атмосферное давление.
Сила гидростатического давления жидкости на плоские поверхности
1. Поверхность горизонтальна
Все точки горизонтальной площадки
находятся на одинаковой глубине и
испытывают одинаковое давление со
стороны покоящейся жидкости. Если
свободная поверхность жидкости открыта
в атмосферу (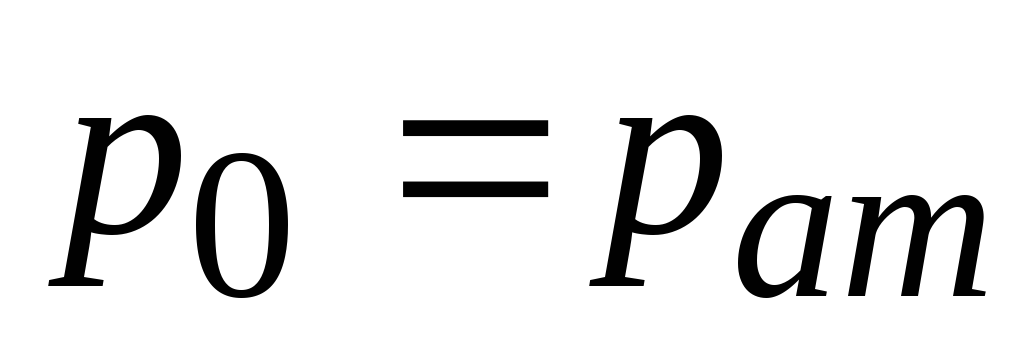 ),
то сила избыточного давления на площадку
площади
),
то сила избыточного давления на площадку
площади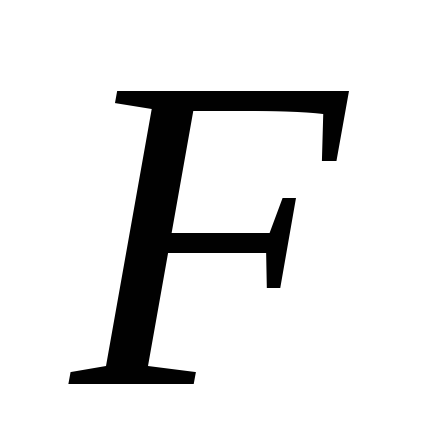 определяется
по формуле
определяется
по формуле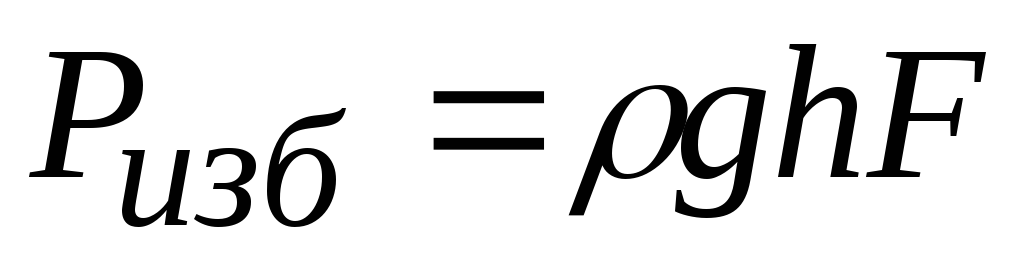 ,
т.е. численно равна весу жидкости,
заключенной в вертикальной призме с
основанием
,
т.е. численно равна весу жидкости,
заключенной в вертикальной призме с
основанием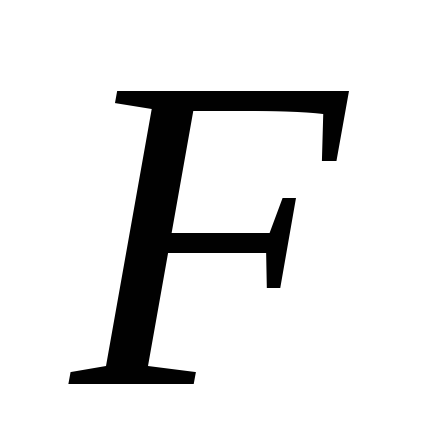 и
высотой
и
высотой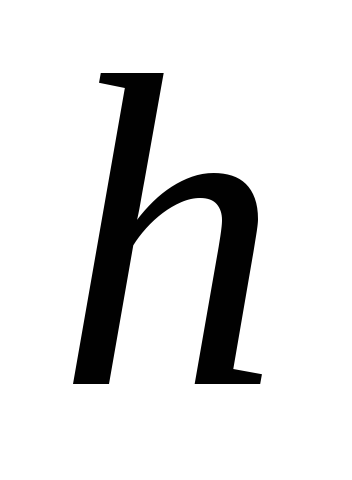 .
.
|
|
Сила
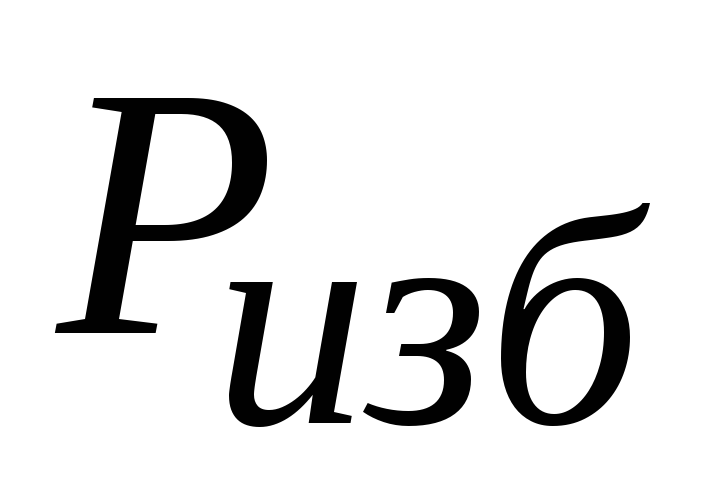 направлена
со стороны жидкости перпендикулярно
стенке.Линия действия силы пересекает
площадку
направлена
со стороны жидкости перпендикулярно
стенке.Линия действия силы пересекает
площадку
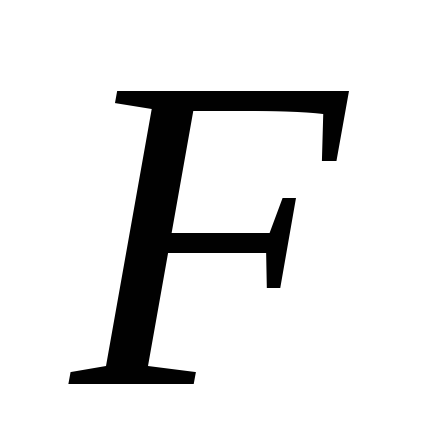 в
центре тяжести, так как давление
распределено по площадке равномерно.
При равенстве
в
центре тяжести, так как давление
распределено по площадке равномерно.
При равенстве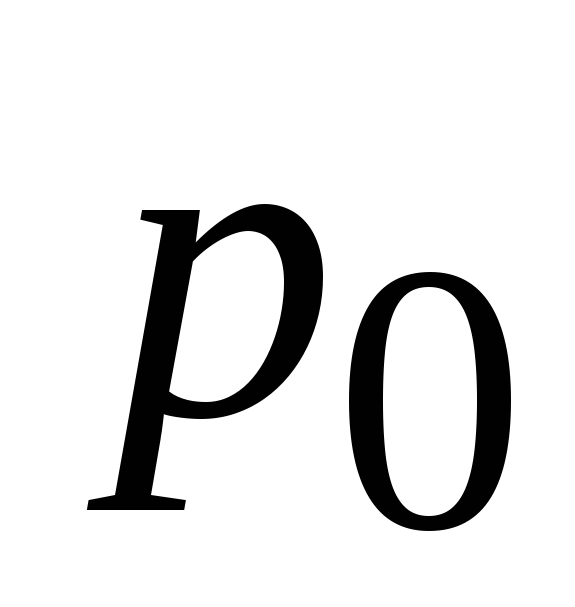 ,
плотностей
,
плотностей ,
площадей оснований
,
площадей оснований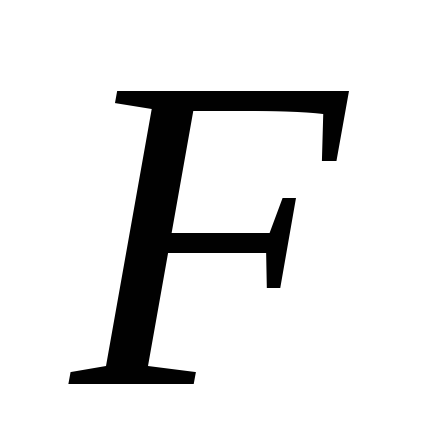 и
глубин
и
глубин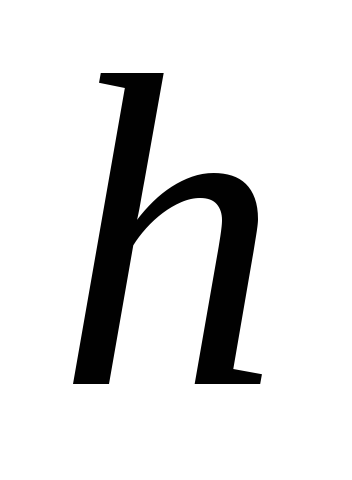 независимо от формы сосуда сила давления
на горизонтальное дно будет одной и той
же. Так в расширяющихся кверху сосудах
сила давления на дно меньше веса жидкости,
в цилиндрических – они одинаковы, а в
сужающихся кверху – сила давления
больше веса заключенной в сосуд жидкости.
Это явление, парадоксальное с точки
зрения житейских представлений, носит
название «гидростатический парадокс».
(Б. Паскаль).
независимо от формы сосуда сила давления
на горизонтальное дно будет одной и той
же. Так в расширяющихся кверху сосудах
сила давления на дно меньше веса жидкости,
в цилиндрических – они одинаковы, а в
сужающихся кверху – сила давления
больше веса заключенной в сосуд жидкости.
Это явление, парадоксальное с точки
зрения житейских представлений, носит
название «гидростатический парадокс».
(Б. Паскаль).
2. Поверхность наклонна
|
|
Рассмотрим
плоскую фигуру площадью
|
Очевидно
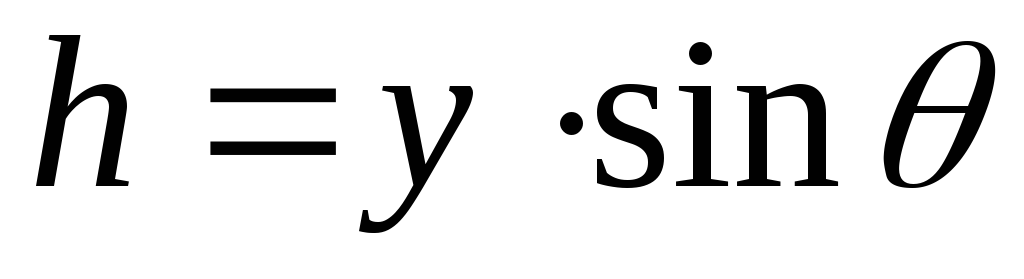 ,
причем
,
причем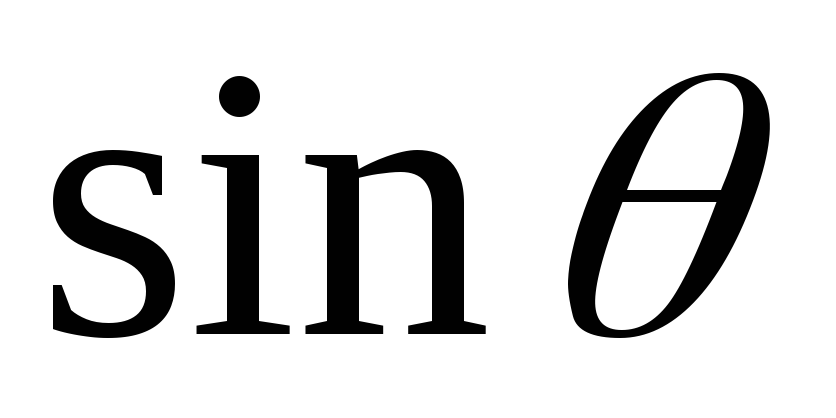 величина
постоянная, выносится за знак интеграла.
величина
постоянная, выносится за знак интеграла.
Известно, что интеграл
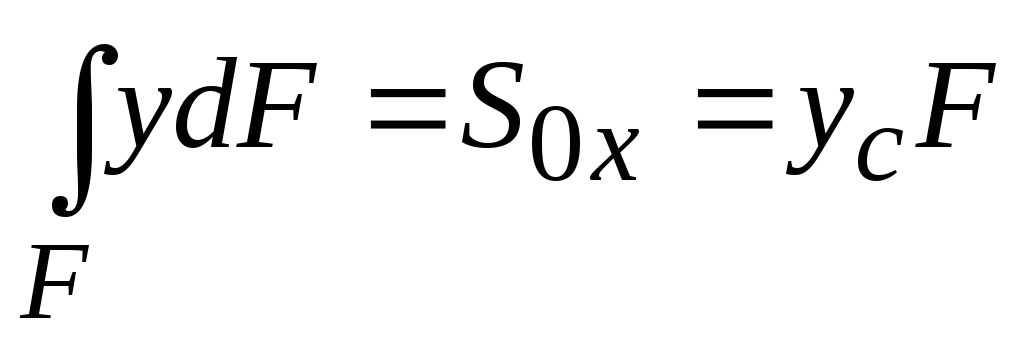 есть
статический момент плоской фигуры
относительно оси
есть
статический момент плоской фигуры
относительно оси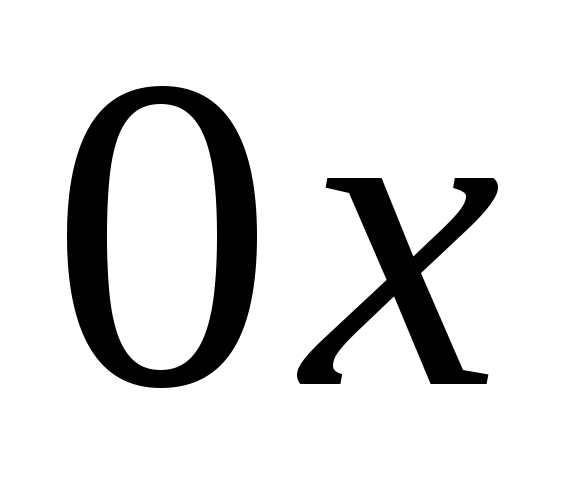 и равен произведению координаты центра
тяжести плоской фигуры на ее площадь.
и равен произведению координаты центра
тяжести плоской фигуры на ее площадь.
Воспользуемся соотношениями
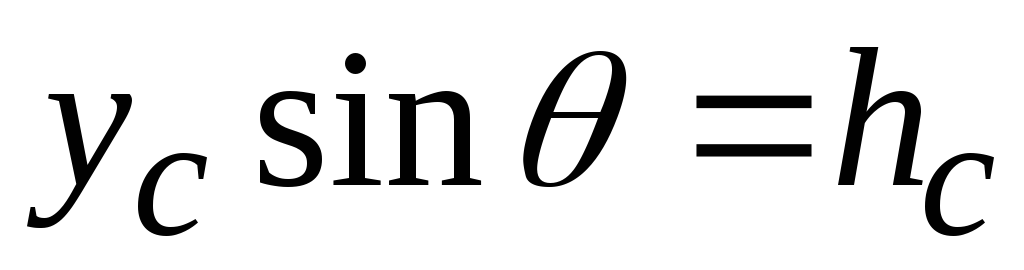 и
и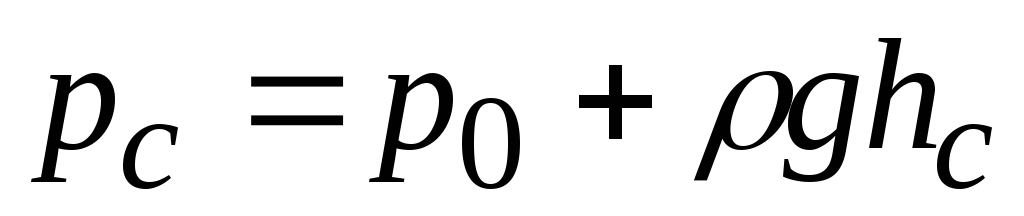 :
:
Сила, действующая на плоскую стенку со
стороны жидкости, равна произведению
давления в центре тяжести на площадь.
Центр давления –
точка приложения
равнодействующей силы давления жидкости
на плоскую поверхность (точка ).
).
Для нахождения координаты
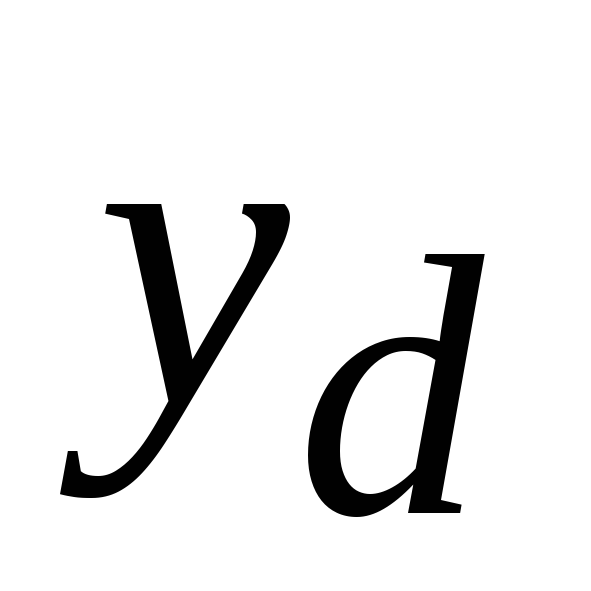 воспользуемся
теоремой Вариньона 1 рассматривая момент сил относительно
оси
воспользуемся
теоремой Вариньона 1 рассматривая момент сил относительно
оси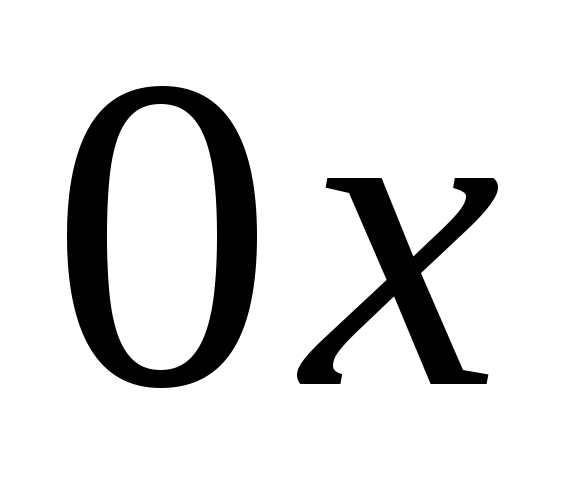 (на
рисунке точка
(на
рисунке точка![]() ).
).
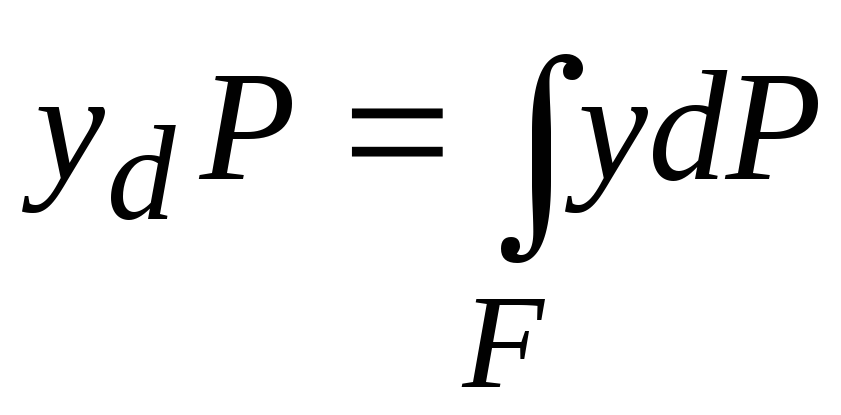 Отсюда находим
Отсюда находим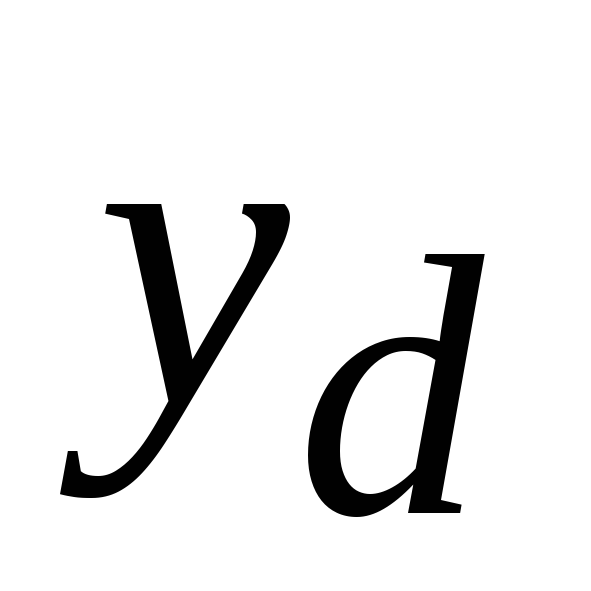 :
:
Известно, что момент инерции плоской
фигуры относительно оси
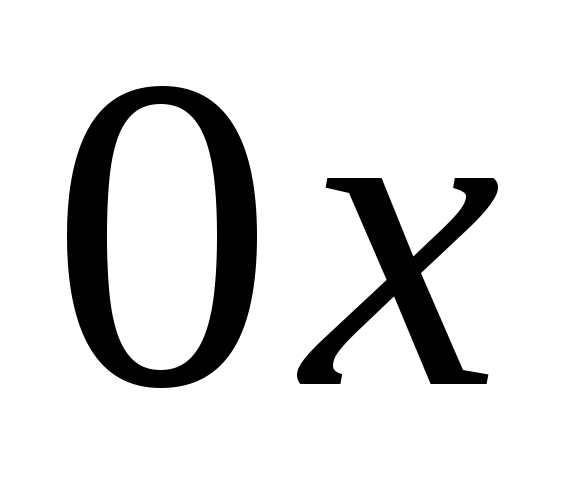
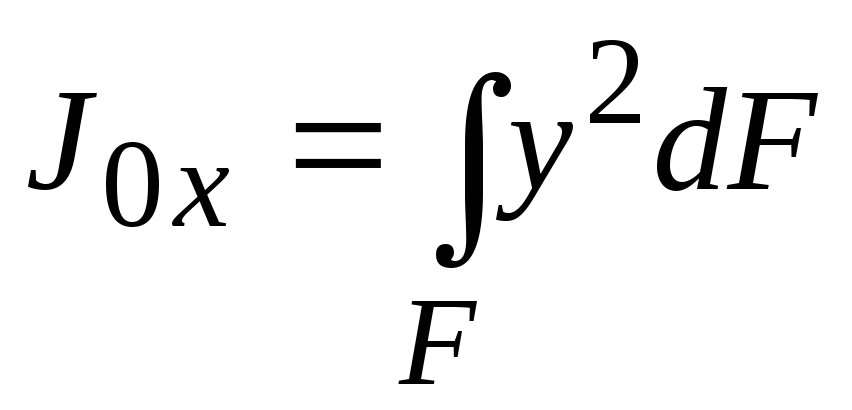 выразим через момент инерции плоской
фигуры относительно оси, приходящей
через центр тяжести (параллельный
перенос оси)
выразим через момент инерции плоской
фигуры относительно оси, приходящей
через центр тяжести (параллельный
перенос оси)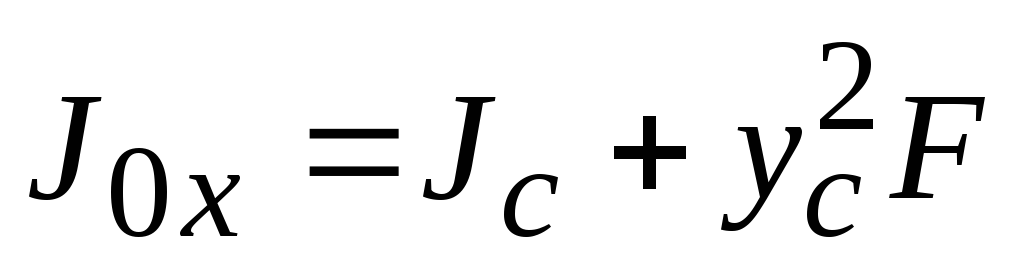 .
Окончательно:
.
Окончательно:
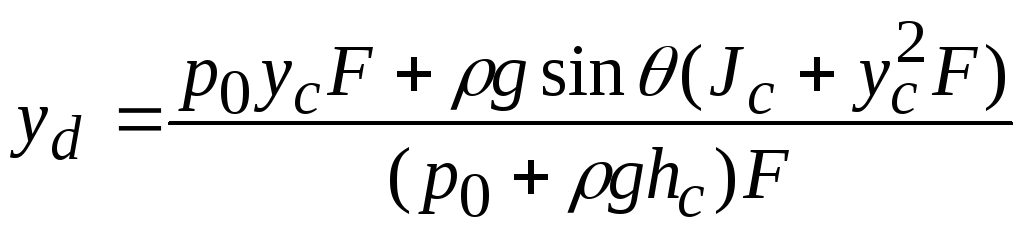 .
.
Если стенка вертикальная, то формула
упрощается, т.к.
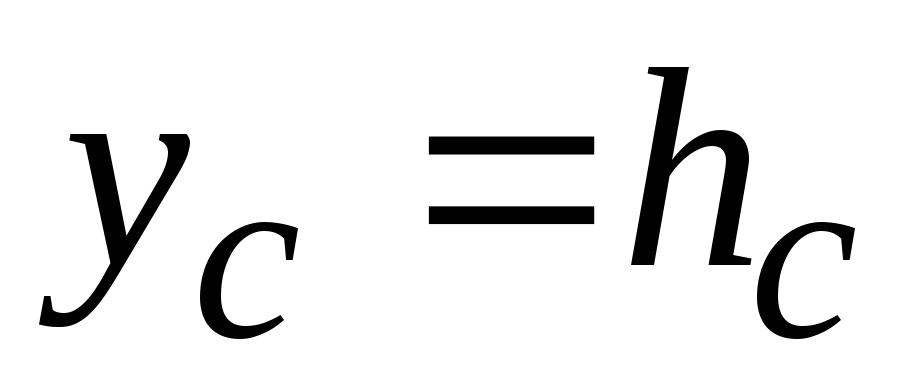 ,
,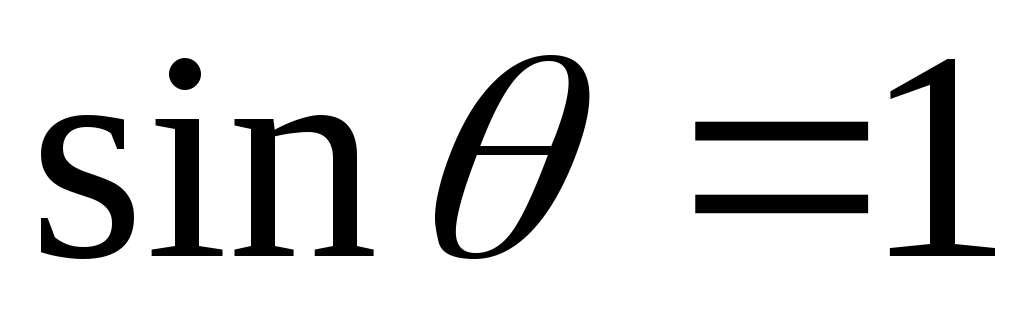 :
:
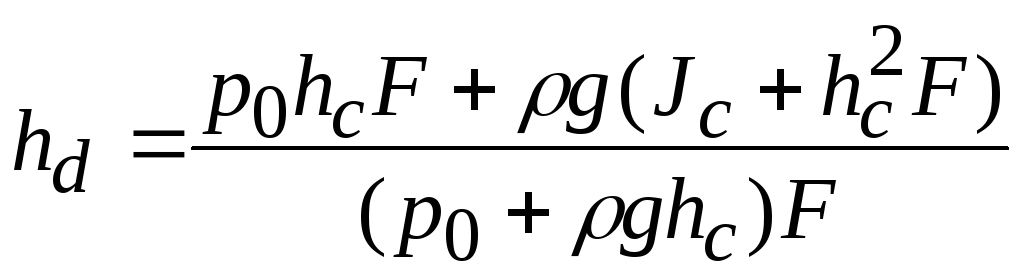 .
.
Если на поверхности жидкости избыточное
давление равно нулю (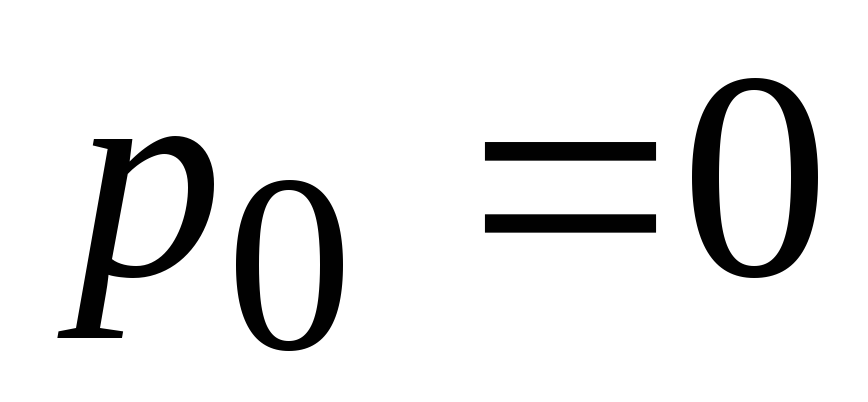 ),
то формула упрощается
),
то формула упрощается
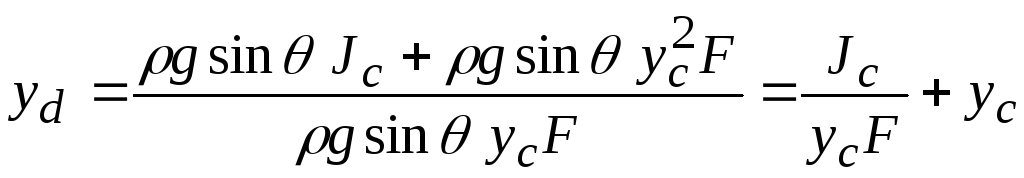
Окончательно координата центра давления
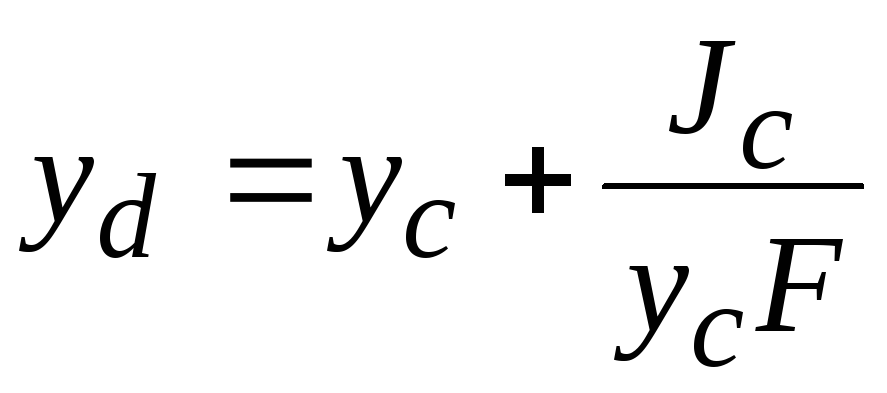
Величину
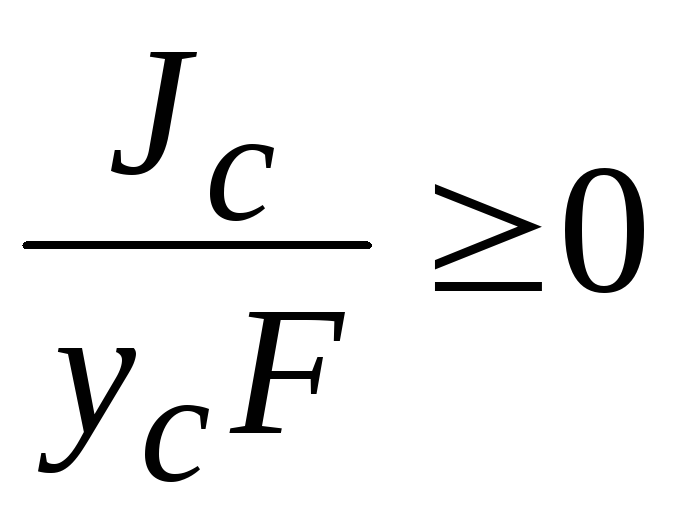 называют эксцентриситетом. Напомним:
называют эксцентриситетом. Напомним: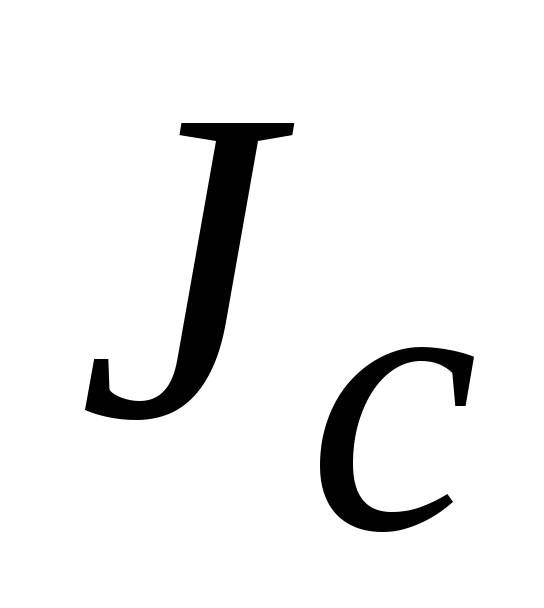 –
момент инерции плоской фигуры относительно
горизонтальной оси, проходящей через
центр тяжести.
–
момент инерции плоской фигуры относительно
горизонтальной оси, проходящей через
центр тяжести.
Моменты инерции плоских фигур относительно горизонтальной оси, проходящей через центр тяжести (для справки)
|
|
|
|
|
|
Прямоугольник |
|
|
|
|
|
|
|
Сила гидростатического давления жидкости на криволинейные стенки
Рассмотрим некоторую ограниченную
часть твердой цилиндрической поверхности
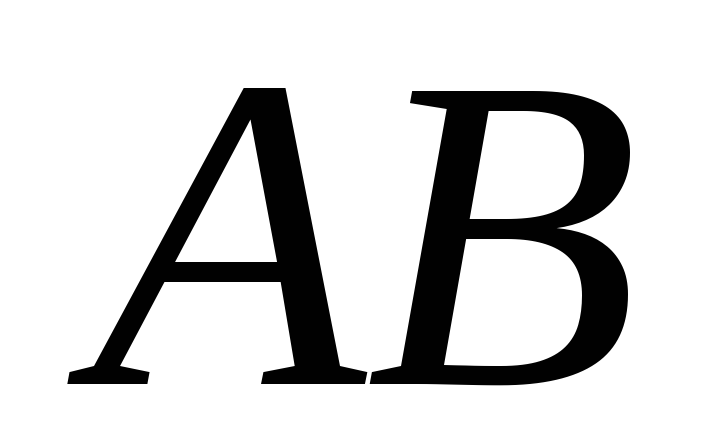 ,
которую назовем цилиндрической стенкой.
Образующая стенки параллельна оси
,
которую назовем цилиндрической стенкой.
Образующая стенки параллельна оси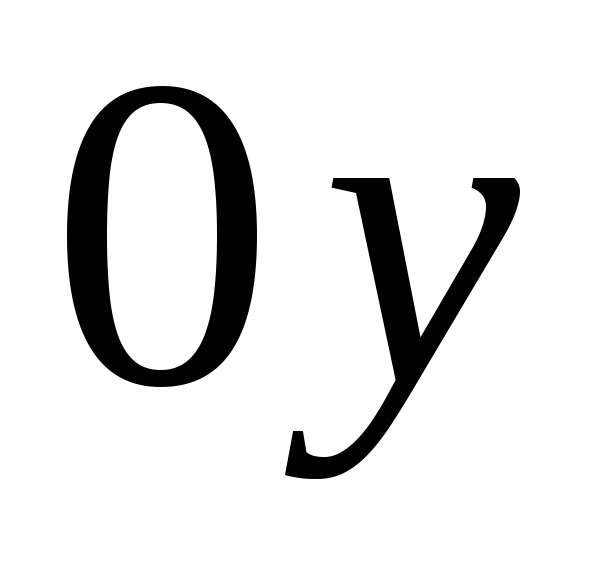 .
.
|
|
Пусть рассматриваемая стенка находится под односторонним воздействием покоящейся жидкости. Выделим
элементарную площадку
Нормально к площадке
со стороны жидкости действует сила
|
Элементарная сила равна произведению давления на площадь
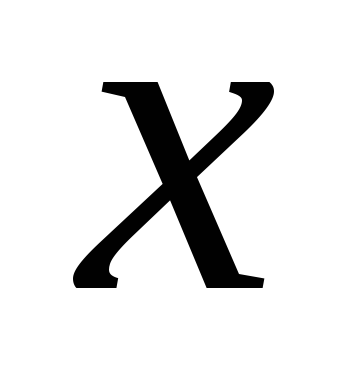 ,
учитывая, что
,
учитывая, что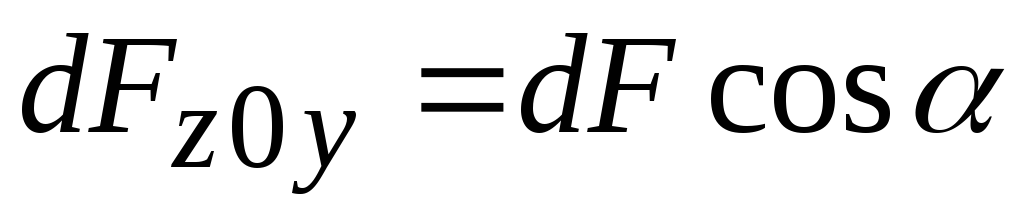
Проекция элементарной силы на ось
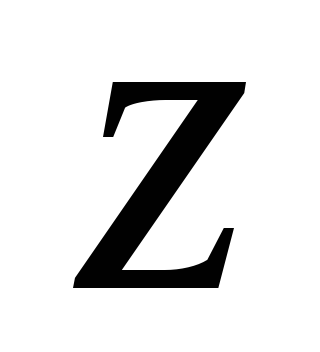 ,
учитывая, что
,
учитывая, что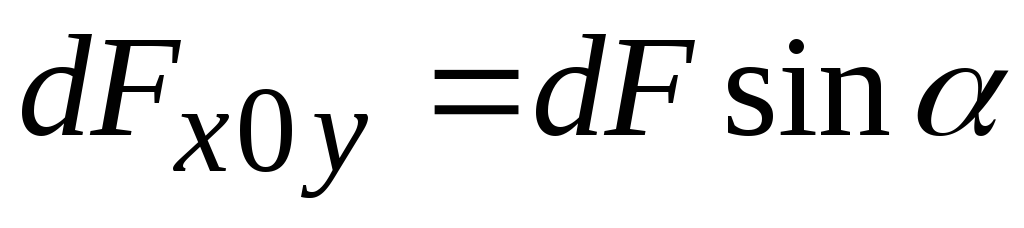
Интегрированием найдем проекции силы,
действующей на всю площадь стенки
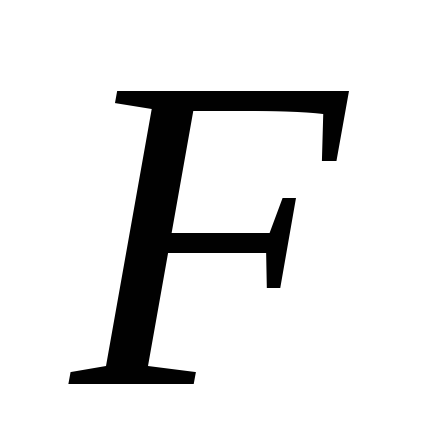 .
.
На ось
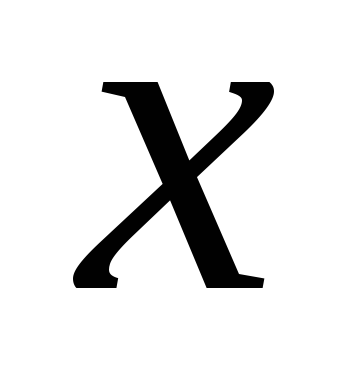 :
:
Учтем выражение для статического момента
плоской фигуры
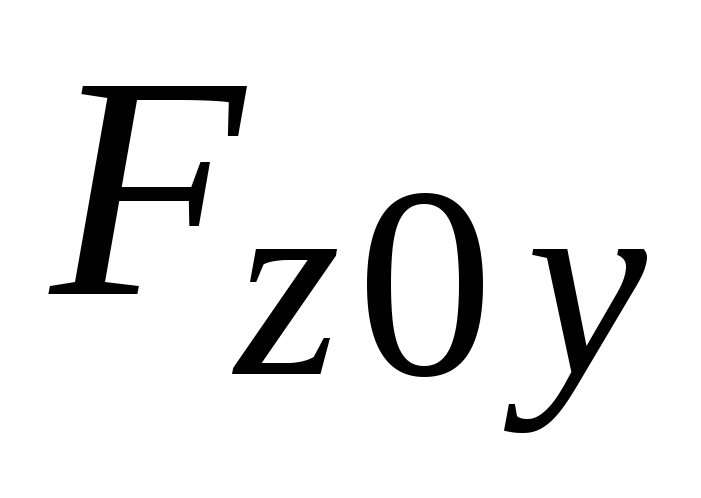 относительно оси
относительно оси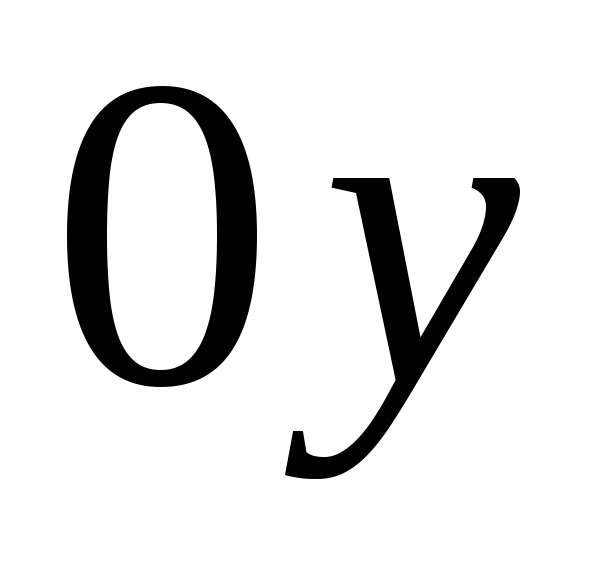
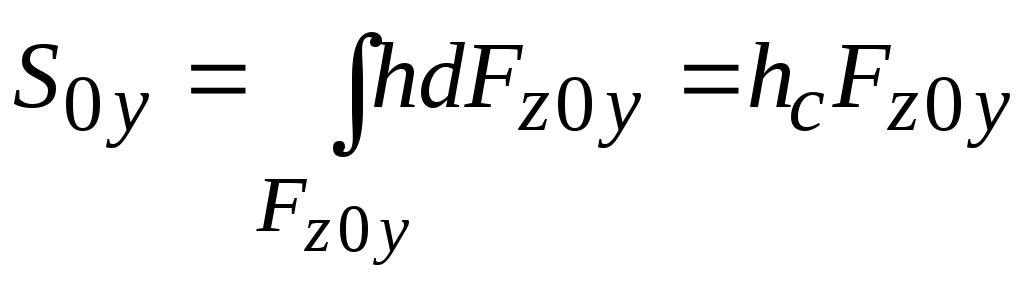 ,
,
где
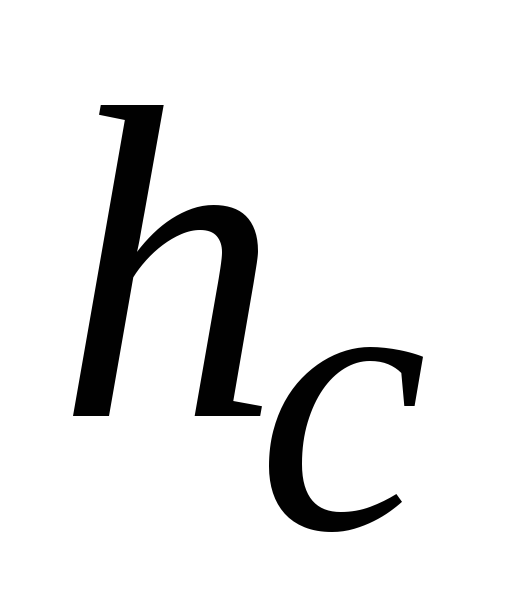 –
глубина погружения центра тяжести
проекции
–
глубина погружения центра тяжести
проекции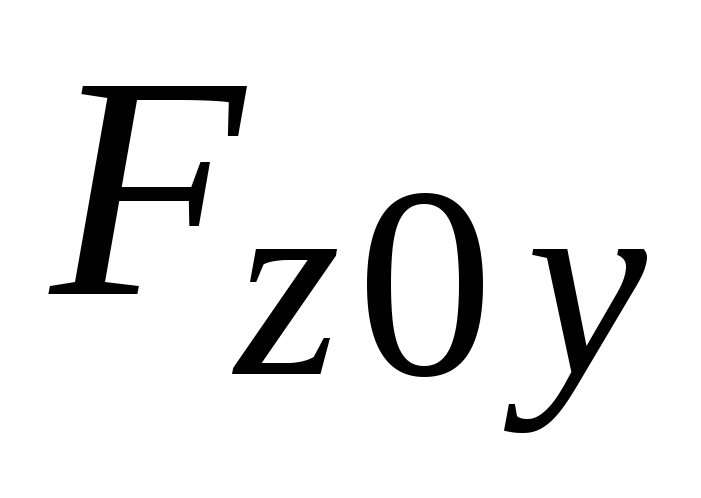 .
.
На ось
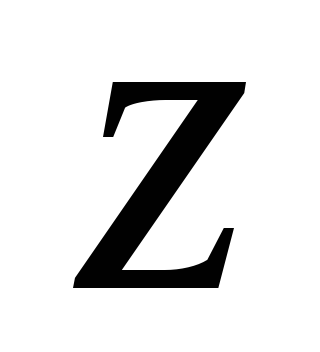 :
:
Заметим, что
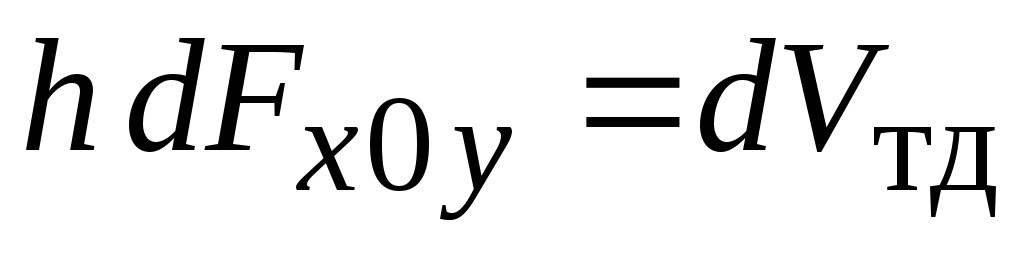 –
объем призмы высотой
–
объем призмы высотой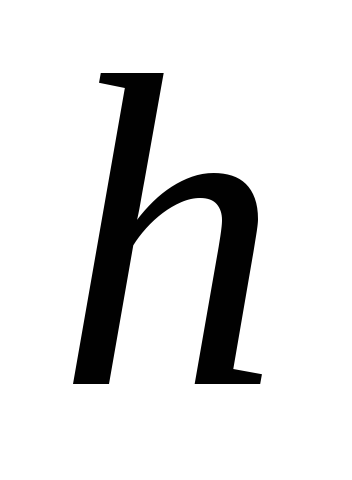 ,
опирающейся на площадку
,
опирающейся на площадку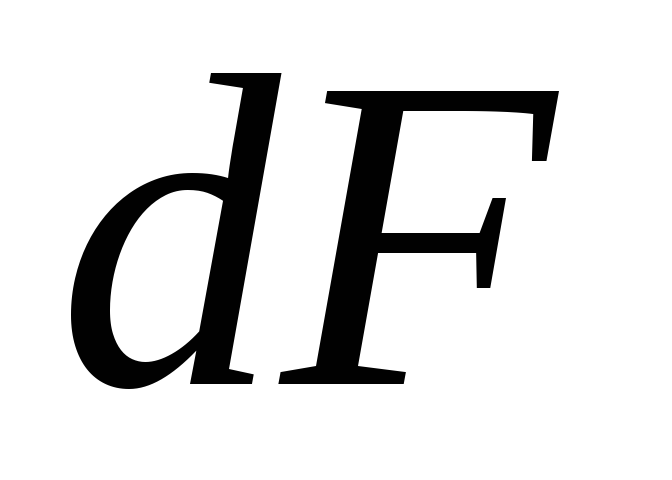 и ограниченной сверху свободной
поверхностью жидкости.
и ограниченной сверху свободной
поверхностью жидкости.
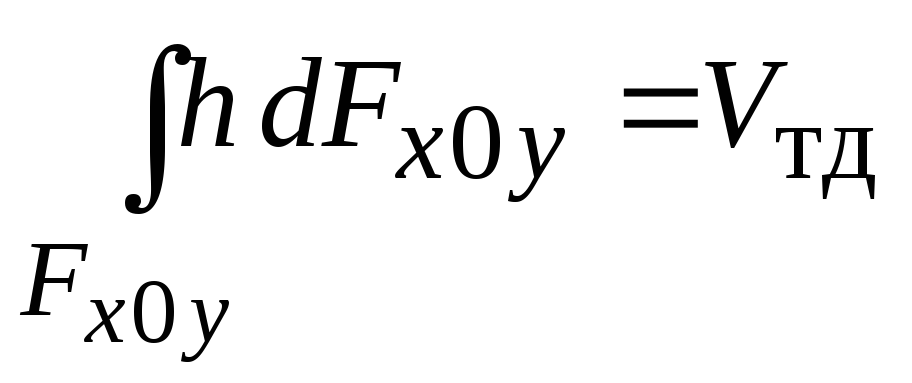 – объем «тела давления».
– объем «тела давления».
Определение. Тело давления – призма, ограниченная снизу криволинейной поверхностью, с боков вертикальными плоскостями, проходящими через крайние образующие поверхности, сверху поверхностью жидкости (или ее продолжением).
Здесь
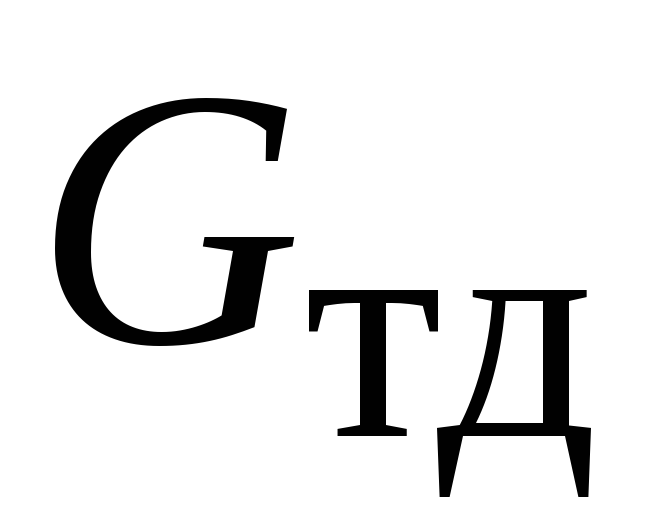 –
вес жидкости в объеме тела давления.
–
вес жидкости в объеме тела давления.
|
|
Окончательно:
|
Если давление на свободной поверхности
равно атмосферному, то избыточное
давление
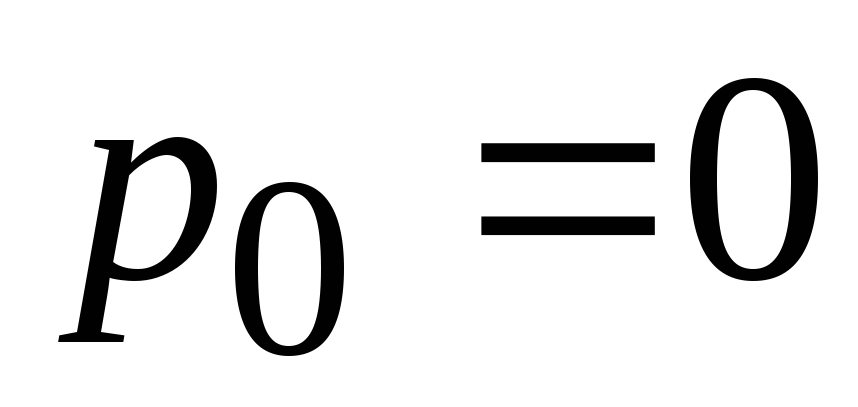 и формулы упрощаются:
и формулы упрощаются: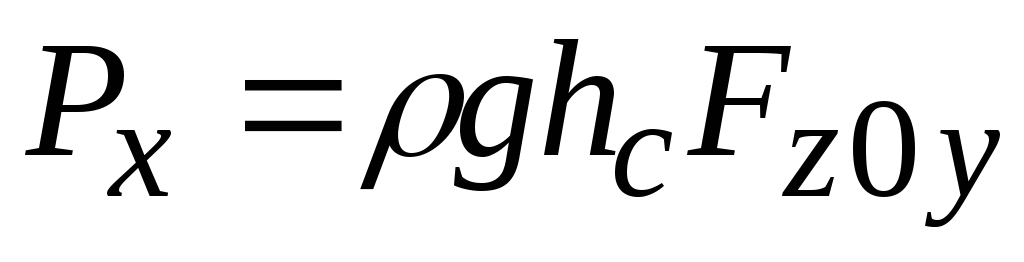 и
и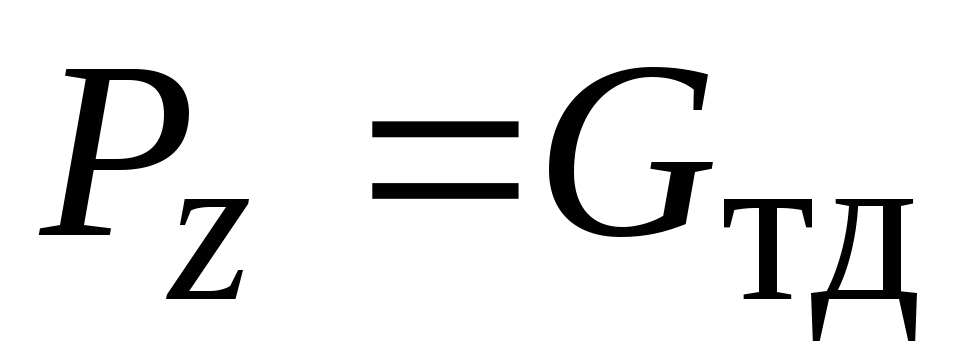
Линия действия
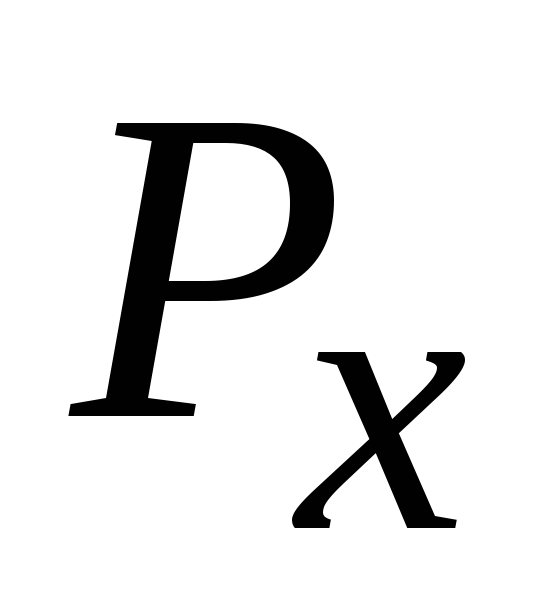 проходит
через центр давления (точка
проходит
через центр давления (точка )
площади проекции
)
площади проекции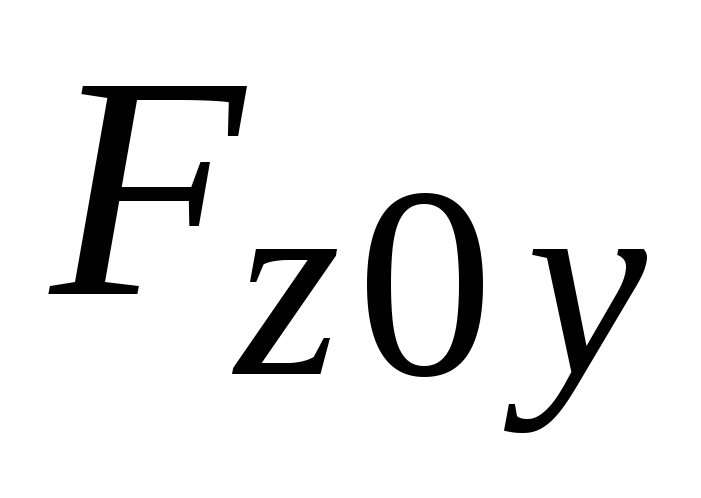 ,
,
а линия действия силы
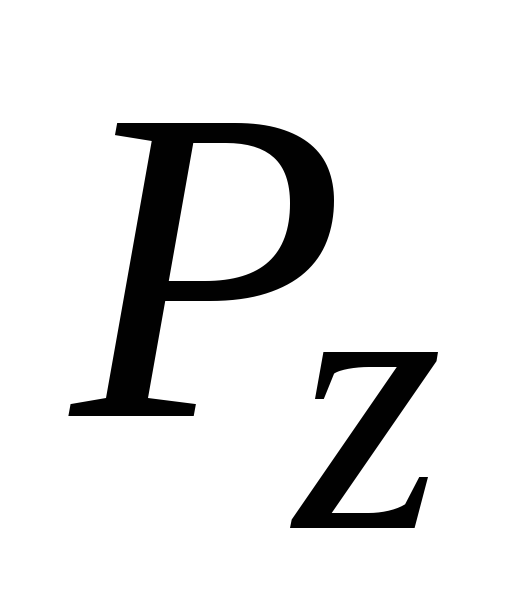 проходит
через центр тяжести тела давления.
проходит
через центр тяжести тела давления.
|
|
Если тело давления
и жидкость находятся с одной стороны
поверхности (жидкость заполняет тело
давления), то сила
|
|
|
Если тело давления
и жидкость находятся с разных сторон
поверхности (жидкость не заполняет
тело давления), то сила
|
Закон Архимеда
Формулировка. Сила давления покоящейся жидкости на тело, погруженное в нее, равна весу вытесненной телом жидкости, направлена вверх и приложена в центре тяжести вытесненного объема.
|
|
Доказательство проведем, используя вывод для силы давления на криволинейную стенку. Рассмотрим
тело, погруженное в жидкость. Условно
разделим тело на верхнюю и нижнюю
половины сечением
Сила
давления жидкости на нижнюю половину
направлена вверх и равна весу жидкости
в теле давления
Сила Архимеда
направлена вверх и равна весу жидкости
в объеме
|
Давление жидкости на стенки трубопровода и резервуара
В заключение раздела гидростатики рассмотрим напряжения, возникающие в стенке круглого трубопровода, находящегося под давлением жидкости.
|
|
Рассмотрим отрезок трубы длиной
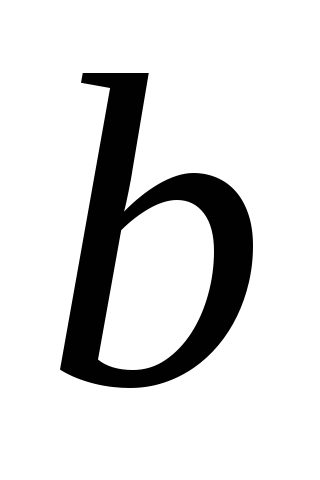 .
Сила давления жидкости на стенку
трубопровода есть произведение давления
.
Сила давления жидкости на стенку
трубопровода есть произведение давления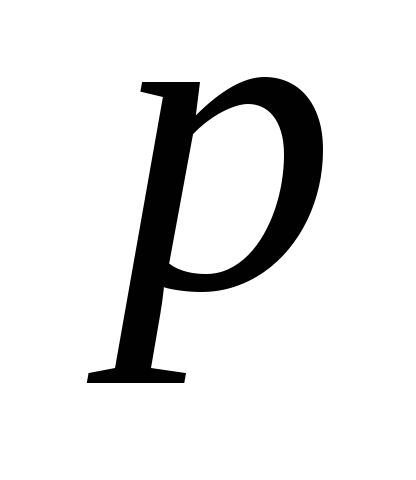 на площадь действия
на площадь действия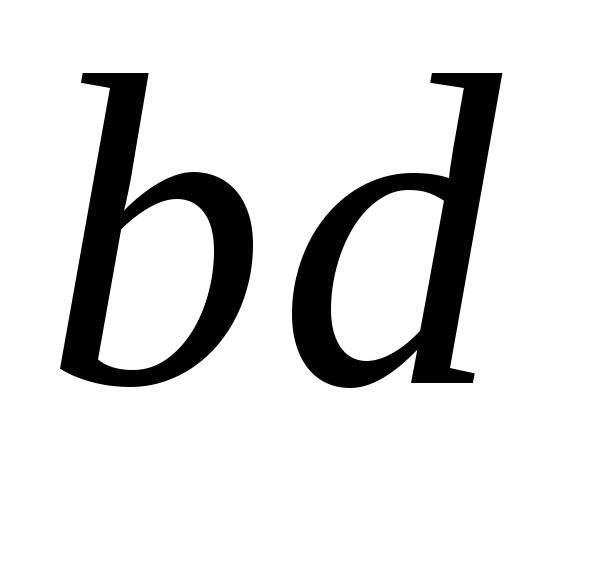 :
: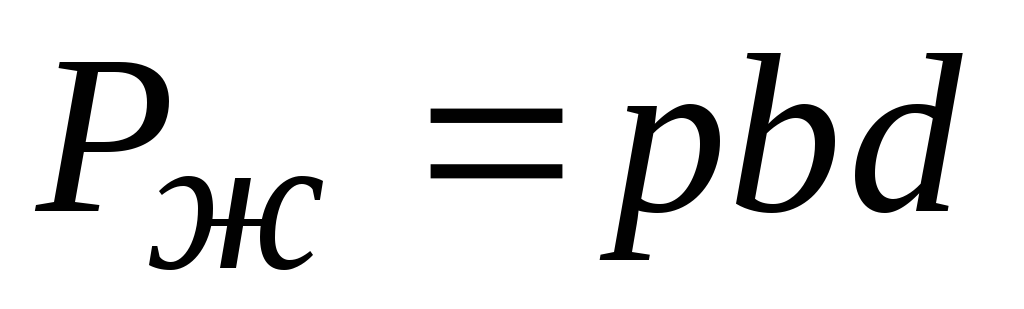 .
.
Эта сила уравновешивается нормальными
растягивающими напряжениями в стенке
трубопровода
 ,
действующими на площади
,
действующими на площади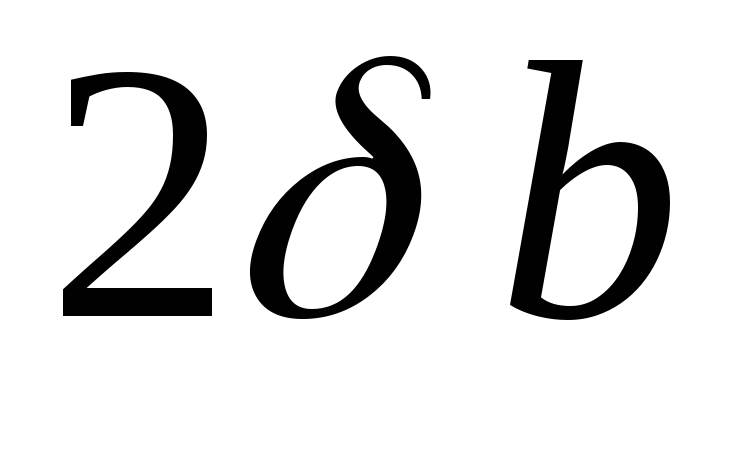 :
: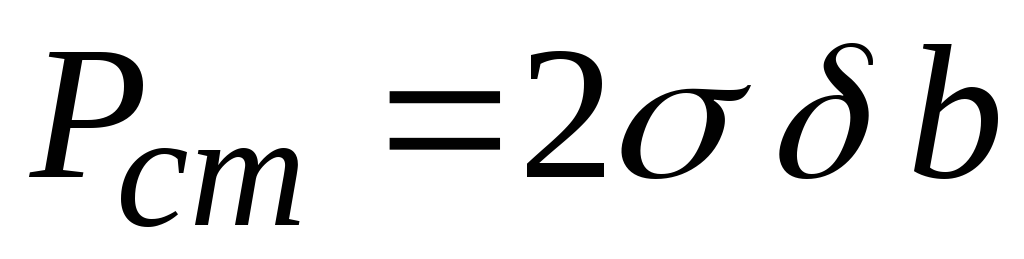
После очевидных преобразований получаем:
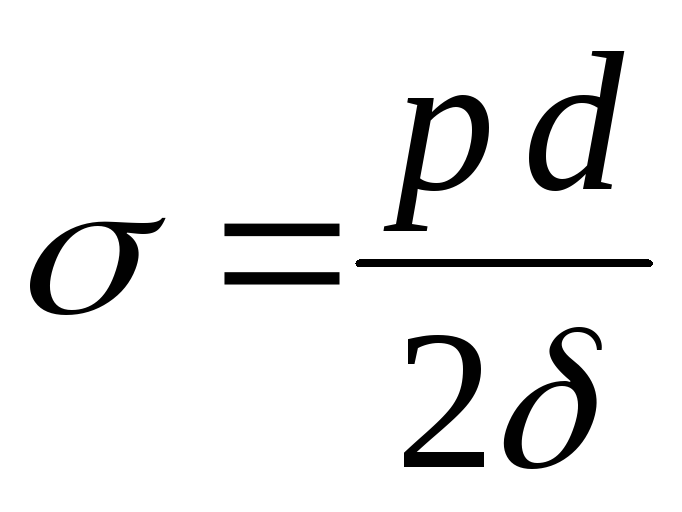
Эта формула, связывающая нормальные
напряжения в стенках трубопровода с
давлением внутри него, называется
«котельной формулой 2 ».
Из нее, зная допустимое напряжение на
разрыв материала стенки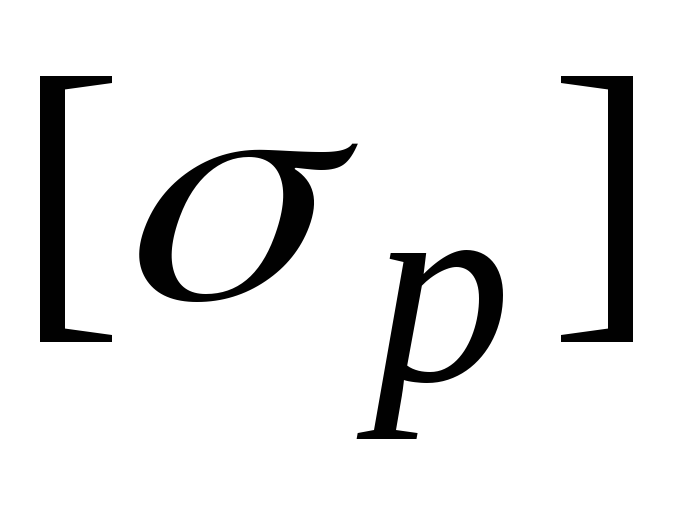 ,
можно найти минимальную толщину стенки
,
можно найти минимальную толщину стенки
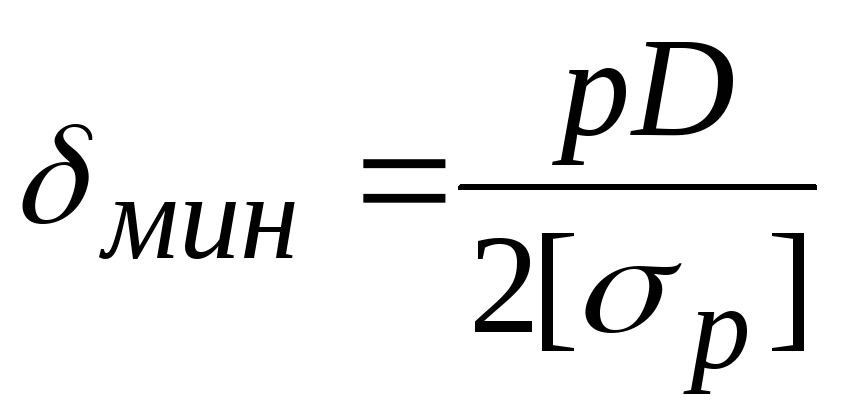 .
При проектировании нужно учесть еще
коэффициент запаса.
.
При проектировании нужно учесть еще
коэффициент запаса.
Выше рассматривались напряжения в стенках, направленные перпендикулярно оси трубопровода. Рассмотрим напряжения, направленные параллельно оси трубопровода.
Давление вдоль оси действует на площадь
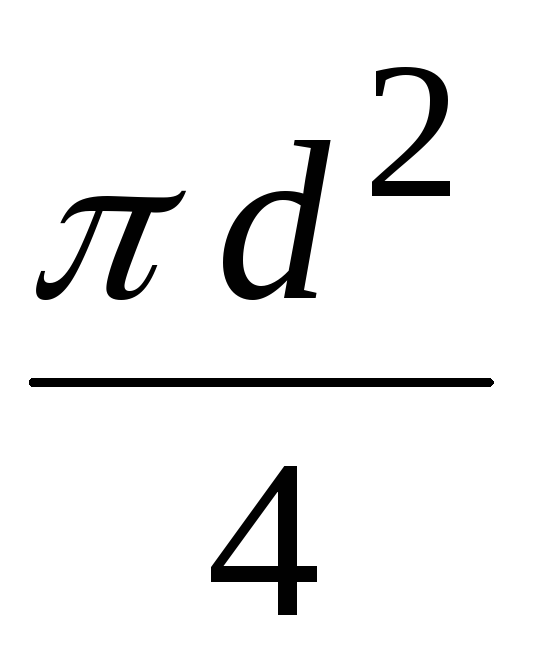 ,
а напряжение в стенке распределено по
площади
,
а напряжение в стенке распределено по
площади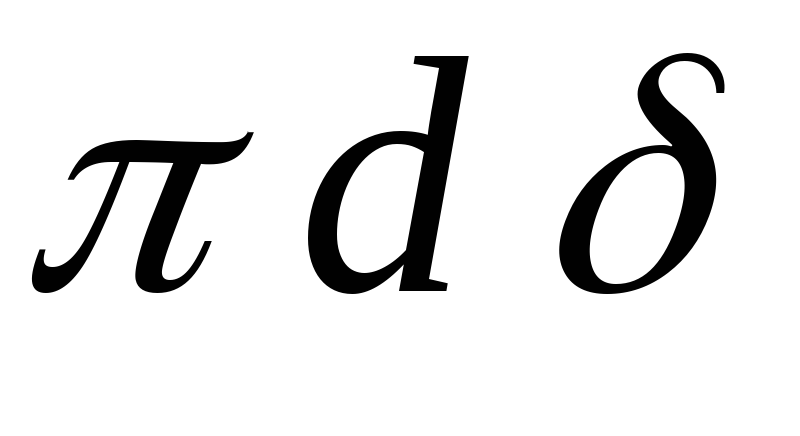 .
Приравняв, получим
.
Приравняв, получим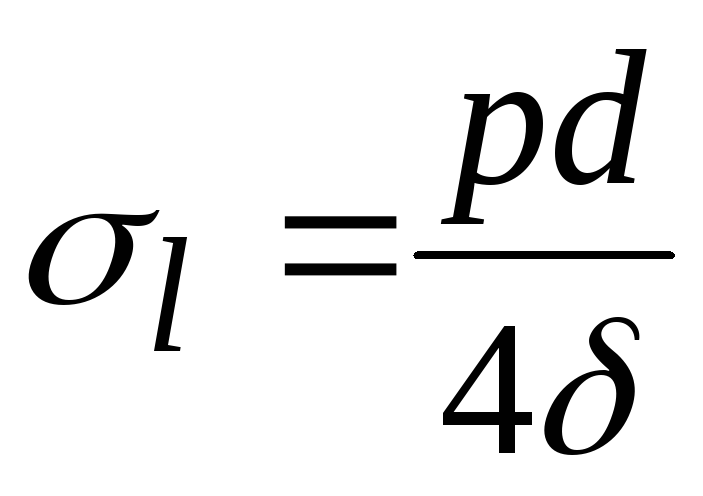 .
Значение напряжения в стенке, направленное
вдоль оси в 2 раза меньше, чем напряжение,
направленное поперек оси. Именно поэтому
сосиски при варке рвутся вдоль, а не
поперек.
.
Значение напряжения в стенке, направленное
вдоль оси в 2 раза меньше, чем напряжение,
направленное поперек оси. Именно поэтому
сосиски при варке рвутся вдоль, а не
поперек.
1Теорема Вариньона. (Пьер Вариньон 1654-1772 французский механик и математик, член Парижской АН)
Если система сил сил F i имеет равнодействующуюR, то моментМ о (F i ) равнодействующей относительно любого центра О (или осиz ) равен сумме моментовM o (F i ) составляющих сил относительно того же центра О (или той же осиz ).
2известна также как формула Мариотта
2.6. Сила давления жидкости па плоскую поверхность, погружённую в жид-кость
Согласно основному закону гидростатики величина давления р
определяется глу-биной погружения точки под уровень свободной поверхности h
жидкости и величиной плотности жидкости р.
Для горизонтальной поверхности
величина давления одинакова во всех точках этой поверхно-сти, т.к.: Отсюда:![]()
![]() Таким образом, Сила давления жидкости на горизонтальную поверхность (дно сосу-да) равно произведению площади этой поверхности на величину давления на глубине по-гружения этой поверхности. На рисунке показан так называемый «гидравлический пара-докс», здесь величины силы давления на дно всех сосудов одинаковы, независимо от формы стенок сосудов и их физической высоты, т.к. площади доньев у всех сосудов оди-наковы, одинаковы и величины давлений. Сила давления на наклонную поверхность, погруженную в жидкость.
Практическим примером такой поверхности может служить наклонная стенка сосуда. Для вывода урав- нения и вычисления силы давления на стенку выберем следующую систему координат: ось ОХ
направим вдоль пересечения плоскости свободной поверхности жидкости с на-клонной стенкой, а ось OZ
направим вдоль этой стенки перпендикулярно оси ОХ.
Тогда в качестве координатной плоскости XOZ
будет выступать сама наклонная стенка. На плос-кости стенки выделим малую площадку, которую, в связи с малыми размерами можем считать горизонтальной. Величина давления на глубине площадки будет равна: где: h
-
глубина погружения площадки относительно свободной поверхности жидкости (по вертика-ли).
Таким образом, Сила давления жидкости на горизонтальную поверхность (дно сосу-да) равно произведению площади этой поверхности на величину давления на глубине по-гружения этой поверхности. На рисунке показан так называемый «гидравлический пара-докс», здесь величины силы давления на дно всех сосудов одинаковы, независимо от формы стенок сосудов и их физической высоты, т.к. площади доньев у всех сосудов оди-наковы, одинаковы и величины давлений. Сила давления на наклонную поверхность, погруженную в жидкость.
Практическим примером такой поверхности может служить наклонная стенка сосуда. Для вывода урав- нения и вычисления силы давления на стенку выберем следующую систему координат: ось ОХ
направим вдоль пересечения плоскости свободной поверхности жидкости с на-клонной стенкой, а ось OZ
направим вдоль этой стенки перпендикулярно оси ОХ.
Тогда в качестве координатной плоскости XOZ
будет выступать сама наклонная стенка. На плос-кости стенки выделим малую площадку, которую, в связи с малыми размерами можем считать горизонтальной. Величина давления на глубине площадки будет равна: где: h
-
глубина погружения площадки относительно свободной поверхности жидкости (по вертика-ли). 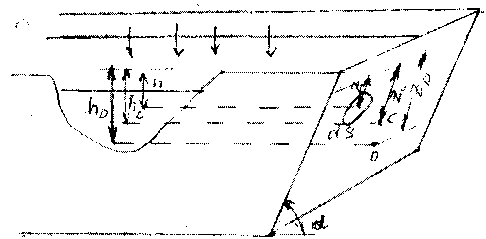 Силадавления
Силадавления![]() dP
на площадку: Для определения силы давления на всю смоченную часть наклонной стенки (часть площади стенки сосуда, расположенная ниже уровня свободной поверхности жидкости) необходимо проинтегрировать это урав-нение по всей смоченной части площади стенки S
.
Интеграл представляет собой статический момент площади S
относительно оси ОХ.
Он, как известно, равен произведению этой площади на координату её центра тяжести z
c
.
Тогда окончательно: Таким образом, сила давления на наклонную плоскую поверхность, погружённую в жидкость равна смоченной площади этой поверхности на величину давления в центре тя-жести этой площади. Сила давления на плоскую стенку кроме величины и направления характеризуется также и точкой приложения этой силы, которая называется центром дав-ления. Центр давления силы атмосферного давления p
0
S
будет находиться в центре тяже-сти площадки, поскольку атмосферное давление передаётся на все точки жидкости одина-ково. Центр давления самой жидкости на площадку можно определить исходя из теоремы о моменте равнодействующей силы. Согласно этой теореме момент равнодействующей силы относительно оси ОХ
будет равен сумме моментов составляющих сил относительно этой же оси.
dP
на площадку: Для определения силы давления на всю смоченную часть наклонной стенки (часть площади стенки сосуда, расположенная ниже уровня свободной поверхности жидкости) необходимо проинтегрировать это урав-нение по всей смоченной части площади стенки S
.
Интеграл представляет собой статический момент площади S
относительно оси ОХ.
Он, как известно, равен произведению этой площади на координату её центра тяжести z
c
.
Тогда окончательно: Таким образом, сила давления на наклонную плоскую поверхность, погружённую в жидкость равна смоченной площади этой поверхности на величину давления в центре тя-жести этой площади. Сила давления на плоскую стенку кроме величины и направления характеризуется также и точкой приложения этой силы, которая называется центром дав-ления. Центр давления силы атмосферного давления p
0
S
будет находиться в центре тяже-сти площадки, поскольку атмосферное давление передаётся на все точки жидкости одина-ково. Центр давления самой жидкости на площадку можно определить исходя из теоремы о моменте равнодействующей силы. Согласно этой теореме момент равнодействующей силы относительно оси ОХ
будет равен сумме моментов составляющих сил относительно этой же оси. 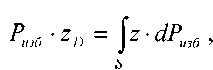 откуда:
откуда: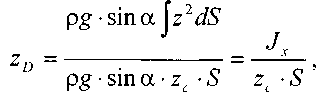 где:- положение центра избыточного давления на вертикальной оси, - момент инерции площадки S
относительно оси ОХ.
Отсюда центр давления (точка приложения равнодействующей силы избыточного давления) расположен всегда ниже центра тяжести площадки. В сучаях, когда внешнней действующей силой на свободную поверхность жидкости является сила атмосферного давления, то на стенку сосуда будут одновременно действовать две одинаковые по вели-чине и противоположные по направлению силы обусловленные атмосферным давлением (на внутреннюю и внешнюю стороны стенки). По этой причине реальной действующей несбалансированной силой остаётся сила избыточного давления. 2.7. Сила давления на криволинейную поверхность, погружённую в жидкость
Выберем внутри покоящейся жидкости криволинейную поверхность ABCD
,
которая может быть частью поверхности некоторого тела погруженного в жидкость. Построим проекции этой поверхности на координатные плоскости. Тогда в координатной плоскости XOZ
проекцией этой поверхности будет плоская поверхность , в координатной плоскости YOZ
-
плоская поверхность
где:- положение центра избыточного давления на вертикальной оси, - момент инерции площадки S
относительно оси ОХ.
Отсюда центр давления (точка приложения равнодействующей силы избыточного давления) расположен всегда ниже центра тяжести площадки. В сучаях, когда внешнней действующей силой на свободную поверхность жидкости является сила атмосферного давления, то на стенку сосуда будут одновременно действовать две одинаковые по вели-чине и противоположные по направлению силы обусловленные атмосферным давлением (на внутреннюю и внешнюю стороны стенки). По этой причине реальной действующей несбалансированной силой остаётся сила избыточного давления. 2.7. Сила давления на криволинейную поверхность, погружённую в жидкость
Выберем внутри покоящейся жидкости криволинейную поверхность ABCD
,
которая может быть частью поверхности некоторого тела погруженного в жидкость. Построим проекции этой поверхности на координатные плоскости. Тогда в координатной плоскости XOZ
проекцией этой поверхности будет плоская поверхность , в координатной плоскости YOZ
-
плоская поверхность![]() и в плоскости свободной поверхности жидкости (координатная плоскость ХОТ) -
плоская поверхность
и в плоскости свободной поверхности жидкости (координатная плоскость ХОТ) -
плоская поверхность ![]() . На криволи- нейной поверхности выделим малую площадку dS
, проекции которой на координатные плоскости будут соответственно
. На криволи- нейной поверхности выделим малую площадку dS
, проекции которой на координатные плоскости будут соответственно ![]() . Сила давления на криво-линейную поверхность dP
будет направ-лена по внутренней нормали к этой по-верхности и может быть представлена в виде: Горизонтальные составляющие мо-гут быть определены, как силы давления "
. Сила давления на криво-линейную поверхность dP
будет направ-лена по внутренней нормали к этой по-верхности и может быть представлена в виде: Горизонтальные составляющие мо-гут быть определены, как силы давления "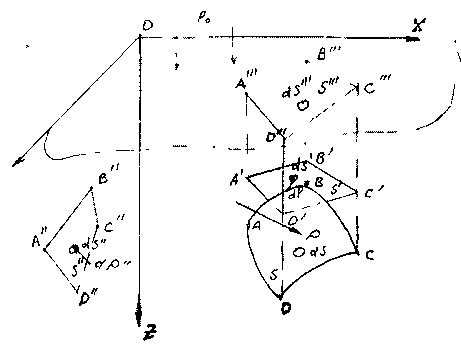 " - на проекции
" - на проекции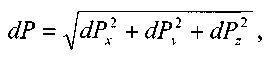 малой площадки dS
на соот- ветствующие координатные плоскости:
малой площадки dS
на соот- ветствующие координатные плоскости:
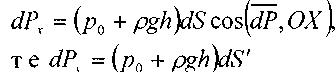
Интегрируя эти уравнения, получим (как в случае с давлением на наклонную по-верхность): 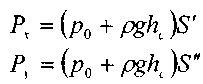 Вертикальная составляющая силы давления: ^
Вертикальная составляющая силы давления: ^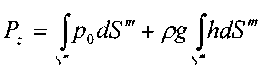 Второй интеграл в этом равенстве представляет собой объём образованный рассмат-риваемой криволинейной поверхностью ABCD
и её проекцией на свободную поверхность жидкости. Этот объём принято называть телом давления Таким образом, горизонтальные составляющие силы давления на криволинейную поверхность равны давлениям на вертикальные проекции этой поверхности, а вертикаль-ная составляющая равна весу тела давления, и силе внешнего давления на горизонтальную проекцию криволинейной поверхности. Основные уравнения гидростатики широко используются на практике. Примероми могут служить простейшие гидравлические машины - гидравлический пресс, построен-ный по принципу сообщающихся сосудов и гидравлический аккумулятор. Гидравлический пресс состоит из двух цилиндров приводного (1) и рабочего (2) со- единеных между собой трубо-проводом и представляет систе-му сообщающихся сосудов. В приводном цилиндре перемеща-ется плунжер малого диаметра d
,
в рабочем цилиндре находит-ся поршень с большим диамет-ром D
.
Связь между плунжером и рабочим поршнем осуществ-
Второй интеграл в этом равенстве представляет собой объём образованный рассмат-риваемой криволинейной поверхностью ABCD
и её проекцией на свободную поверхность жидкости. Этот объём принято называть телом давления Таким образом, горизонтальные составляющие силы давления на криволинейную поверхность равны давлениям на вертикальные проекции этой поверхности, а вертикаль-ная составляющая равна весу тела давления, и силе внешнего давления на горизонтальную проекцию криволинейной поверхности. Основные уравнения гидростатики широко используются на практике. Примероми могут служить простейшие гидравлические машины - гидравлический пресс, построен-ный по принципу сообщающихся сосудов и гидравлический аккумулятор. Гидравлический пресс состоит из двух цилиндров приводного (1) и рабочего (2) со- единеных между собой трубо-проводом и представляет систе-му сообщающихся сосудов. В приводном цилиндре перемеща-ется плунжер малого диаметра d
,
в рабочем цилиндре находит-ся поршень с большим диамет-ром D
.
Связь между плунжером и рабочим поршнем осуществ-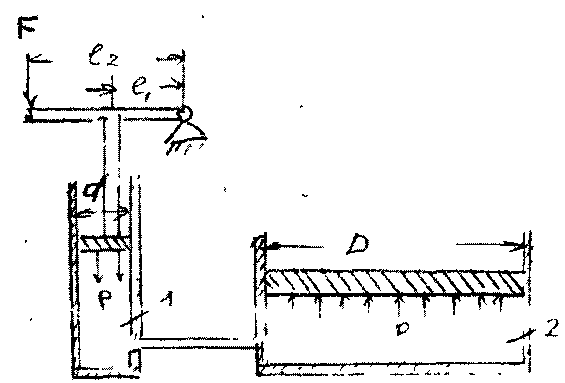 ляется через рабочую жидкость, заполняющую гидравлическую систему (сообщающиеся сосуды). Усилие F
через рычаг передаются рабочей жидкости. Сила давления на жидкость под плунжером Р
]
передаёт жидкости давление р,
которое, в свою очередь, передаётся во все точки рабочего поршня. Тогда сила давления на поверхность рабочего поршеня будет равна"
ляется через рабочую жидкость, заполняющую гидравлическую систему (сообщающиеся сосуды). Усилие F
через рычаг передаются рабочей жидкости. Сила давления на жидкость под плунжером Р
]
передаёт жидкости давление р,
которое, в свою очередь, передаётся во все точки рабочего поршня. Тогда сила давления на поверхность рабочего поршеня будет равна" 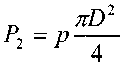 Таким образом, с помощью гидравлического пресса, приложенная к концу рычага ^ сила, увеличивается враз. 2.8. Равновесие твёрдого тела в жидкости
Определим силу давления на твёрдое тело, погружённое в жидкость. На замкнутую криволинейную поверхность, являющуюся поверхностью твердого тела погружённого в жидкость будут действовать массо-вые силы (в данном случае силы тя-жести) и поверхностные, силы дав-ления на поверхность тела. Рассмот-рим действие сил давления. Как из-вестно, горизонтальные составляю-щие силы давления будут взаимно уравновешены. Так как проекции тела на координатную плоскость XOZ
с его левой и правой сторон
Таким образом, с помощью гидравлического пресса, приложенная к концу рычага ^ сила, увеличивается враз. 2.8. Равновесие твёрдого тела в жидкости
Определим силу давления на твёрдое тело, погружённое в жидкость. На замкнутую криволинейную поверхность, являющуюся поверхностью твердого тела погружённого в жидкость будут действовать массо-вые силы (в данном случае силы тя-жести) и поверхностные, силы дав-ления на поверхность тела. Рассмот-рим действие сил давления. Как из-вестно, горизонтальные составляю-щие силы давления будут взаимно уравновешены. Так как проекции тела на координатную плоскость XOZ
с его левой и правой сторон 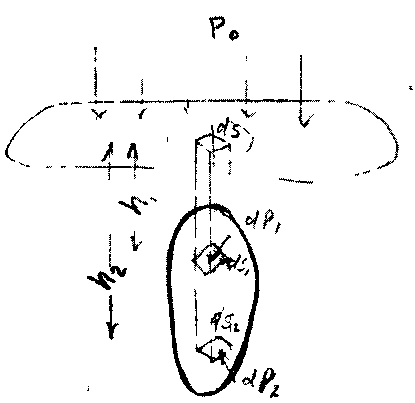 совпадут; то совпадут и координаты центров тяжести этих проекций. То-гда проекции сил давления на ось ОХ
будут одинаковыми по величине, но противоположными по направлению
совпадут; то совпадут и координаты центров тяжести этих проекций. То-гда проекции сил давления на ось ОХ
будут одинаковыми по величине, но противоположными по направлению![]() Аналогично можно записать и для проекций сил давления на ось OY
(давление на проек-ции поверхностей в координатной плоскости YOZ
),
.
Неуравновешенными будут лишь вертикальные составляющие силы давления, действующие на верхнюю и нижнюю стороны поверхности тела. Вертикальными сечениями выделим на верхней и нижней половинах тела малые площадки. Тогда вертикальные составляющие на верхнюю и нижнюю площадки будут равны:
Аналогично можно записать и для проекций сил давления на ось OY
(давление на проек-ции поверхностей в координатной плоскости YOZ
),
.
Неуравновешенными будут лишь вертикальные составляющие силы давления, действующие на верхнюю и нижнюю стороны поверхности тела. Вертикальными сечениями выделим на верхней и нижней половинах тела малые площадки. Тогда вертикальные составляющие на верхнюю и нижнюю площадки будут равны: 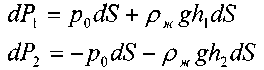 После интегрирования по объёму тела найдём равнодействующую сил давления. Она окажется равной разности весов двух тел давления, ограниченных свободной поверхно-стью жидкости и верхней и нижней поверхностями тела.
После интегрирования по объёму тела найдём равнодействующую сил давления. Она окажется равной разности весов двух тел давления, ограниченных свободной поверхно-стью жидкости и верхней и нижней поверхностями тела. ![]() Равнодействующая сил давления носит название выталкивающей силы, эта сила на-правлена вертикально вверх и численно равна весу жидкости в объёме вытесненной те-лом. Последнее положение получило название закона Архимеда. Закон Архимеда часто формулируют несколько иначе: «тело, погружнное в жидкость теряет в своём весе столько сколько весит вытесненная им жидкость». Таким образом, На погружённое в жидкость тело действуют две силы: вес тела
Равнодействующая сил давления носит название выталкивающей силы, эта сила на-правлена вертикально вверх и численно равна весу жидкости в объёме вытесненной те-лом. Последнее положение получило название закона Архимеда. Закон Архимеда часто формулируют несколько иначе: «тело, погружнное в жидкость теряет в своём весе столько сколько весит вытесненная им жидкость». Таким образом, На погружённое в жидкость тело действуют две силы: вес тела![]() и выталкивающая сила
и выталкивающая сила![]() ЕслиТело будет тонуть. ЕслиТело будет всплывать до тех пор пока вес тела и величина выталкивающей силы, действующей на погруженную часть объёма тела не уравновесятся. ЕслиТело будет находиться во взвешенном состоянии в жидкости, т.е. плавать внутри жидкости на любой заданной глубине. Для тела плавающего на поверхности жидкости должно, таким образом выполняться условие:
ЕслиТело будет тонуть. ЕслиТело будет всплывать до тех пор пока вес тела и величина выталкивающей силы, действующей на погруженную часть объёма тела не уравновесятся. ЕслиТело будет находиться во взвешенном состоянии в жидкости, т.е. плавать внутри жидкости на любой заданной глубине. Для тела плавающего на поверхности жидкости должно, таким образом выполняться условие: ![]() Другими словами, степень погружения плавающего на поверхности тела под уровень жидкости заваисит от со-
Другими словами, степень погружения плавающего на поверхности тела под уровень жидкости заваисит от со-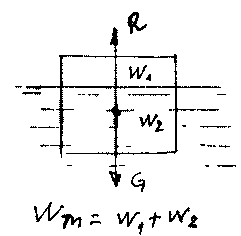 отношения плотности тела
отношения плотности тела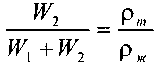 и жидкости: Если тело однородное, то точка приложения силы тяжести тела и точка приложения выталкивающей силы совпадают. В тех случаях, когда плавающее на поверхности жидко-сти тело не однородно по своему составу (корабль с грузом) в условиях равновесия точки приложения действующих на тело сил располагаются в разных местах на прямой верти-кальной линии. В таких случаях на плавающее в жидкости тело действует пара сил, от действия которой зависит положение тела относительно жидкости Такие плавающие тела могут находиться в ос-тойчивом и не остойчивом состоянии Так тело 1 под дей-ствием пары сил находится в состоянии равновесия На тело 2 действует пара сил, стремящаяся уменьшить угол крена (угол между осью плавания тела и плоскостью сво-
и жидкости: Если тело однородное, то точка приложения силы тяжести тела и точка приложения выталкивающей силы совпадают. В тех случаях, когда плавающее на поверхности жидко-сти тело не однородно по своему составу (корабль с грузом) в условиях равновесия точки приложения действующих на тело сил располагаются в разных местах на прямой верти-кальной линии. В таких случаях на плавающее в жидкости тело действует пара сил, от действия которой зависит положение тела относительно жидкости Такие плавающие тела могут находиться в ос-тойчивом и не остойчивом состоянии Так тело 1 под дей-ствием пары сил находится в состоянии равновесия На тело 2 действует пара сил, стремящаяся уменьшить угол крена (угол между осью плавания тела и плоскостью сво-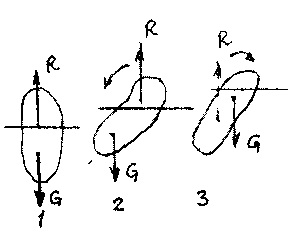 бодной поверхности жидкости) Такое положение пла-вающего тела называется остойчивым На тело 3 действует пара сил, стремящаяся увели-чить угол крена (перевернуть тело), такое положение тела называется не остойчивым по-ложением ;
t
*
3. Элементы кинематики жидкости
Кинематикой называют раздел механики, изучающий движение физических тел во-обще, вне связи с источником движения (силами). Это определение справедливо и для ки-нематики жидкости как отдельного раздела гидравлики. 3.1. Методы изучения движения жидкости.
Жидкость представляет собой физическое тело, состоящее из бесконечно большого числа бесконечно малых частиц. С большой степенью точности мы можем рассматривать жидкое тело как сплошную среду, эта модель позволяет значительно упростить решение большинства гидравлических задач. Тем не менее, нередки случаи, когда уровень иссле-дования движения жидкого тела требует глубокого знания физических процессов проис-ходящих в движущейся жидкости на молекулярном уровне. В таких случаях вполне удоб-ная модель сплошной среды может оказаться неприемлемой. Исходя из практики изучения гидравлики как прикладной дисциплины, можно упо-мянуть два метода изучения движения жидкости: метод Лагранжа и метод Эйлера. Описание движения жидкости методом Лагранжа сво-дится к рассмотрению положения частиц жидкости (в пол-ном смысле слова) в любой момент времени. Так в началь-ный момент времени частицы находились в точках 1, 2, 3 и 4. По истечении некоторого времени они переместились в точки: Г, 2",3"и4", причём это перемещение сопровожда-лось изменением объёмов и форм частиц (упругой деформа-цией). Тогда можно утверждать, что частицы жидкости при
бодной поверхности жидкости) Такое положение пла-вающего тела называется остойчивым На тело 3 действует пара сил, стремящаяся увели-чить угол крена (перевернуть тело), такое положение тела называется не остойчивым по-ложением ;
t
*
3. Элементы кинематики жидкости
Кинематикой называют раздел механики, изучающий движение физических тел во-обще, вне связи с источником движения (силами). Это определение справедливо и для ки-нематики жидкости как отдельного раздела гидравлики. 3.1. Методы изучения движения жидкости.
Жидкость представляет собой физическое тело, состоящее из бесконечно большого числа бесконечно малых частиц. С большой степенью точности мы можем рассматривать жидкое тело как сплошную среду, эта модель позволяет значительно упростить решение большинства гидравлических задач. Тем не менее, нередки случаи, когда уровень иссле-дования движения жидкого тела требует глубокого знания физических процессов проис-ходящих в движущейся жидкости на молекулярном уровне. В таких случаях вполне удоб-ная модель сплошной среды может оказаться неприемлемой. Исходя из практики изучения гидравлики как прикладной дисциплины, можно упо-мянуть два метода изучения движения жидкости: метод Лагранжа и метод Эйлера. Описание движения жидкости методом Лагранжа сво-дится к рассмотрению положения частиц жидкости (в пол-ном смысле слова) в любой момент времени. Так в началь-ный момент времени частицы находились в точках 1, 2, 3 и 4. По истечении некоторого времени они переместились в точки: Г, 2",3"и4", причём это перемещение сопровожда-лось изменением объёмов и форм частиц (упругой деформа-цией). Тогда можно утверждать, что частицы жидкости при ![]() своём движении участвуют в трёх видах движения (поступа-тельном, вращательном и деформации). Для описания такого сложного движения жидко-сти необходимо, таким образом, определить как траектории частиц, так и гидравлические характеристики частиц (плотность р,
температуру Т
и скорость и)
в функции времени и координат.
своём движении участвуют в трёх видах движения (поступа-тельном, вращательном и деформации). Для описания такого сложного движения жидко-сти необходимо, таким образом, определить как траектории частиц, так и гидравлические характеристики частиц (плотность р,
температуру Т
и скорость и)
в функции времени и координат. 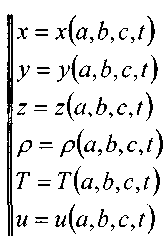 Переменные а, Ь, с,
и / носят название переменных Лагранжа. Задача сводится к ре-шению систем дифференциальных уравнений в частных производных для каждой части- цы жидкости. Метод Лагранжа ввиду громоздкости и трудности решения может исполь-зоваться в случаях детального изучения поведения лишь отдельных частиц жидкости. Ис-пользование этого метода для инженерных расчётов не рентабельно. Суть другого метода, метода Эйлера заключается в том, что движение жидкости подменяется изменением поля скоростей. Под полем скоростей понимают некоторую дос-таточно большую совокупность точек бесконечного пространства занятого движущейся жидкостью, когда в каждой точке пространства в каждый момент времени находится час-тица жидкости с определённой скоростью (вектором скорости). Припишем неподвижным точкам пространства скорость частиц жидкости, которые в данный момент времени нахо-дятся в этих точках. Поскольку пространство бесконечно и непрерывно, то мы имеем мас-сив данных о скоростях достаточно полный, чтобы определить (задать) поле в каждой его точке. Условно, нос достаточной точностью такое поле можно считать непрерывным. Несмотря на то, что исходные условия создания модели движущийся жидкости до-вольно сложные, тем не менее, метод Эйлера весьма удобен для расчётов. Построение поля скоростей осуществляет-ся следующим образом: На некоторый момент времени (например, to
)
произвольным образом выберем необходимое число точек, в которых находятся частицы жид-кости. Приписав их скорости
Переменные а, Ь, с,
и / носят название переменных Лагранжа. Задача сводится к ре-шению систем дифференциальных уравнений в частных производных для каждой части- цы жидкости. Метод Лагранжа ввиду громоздкости и трудности решения может исполь-зоваться в случаях детального изучения поведения лишь отдельных частиц жидкости. Ис-пользование этого метода для инженерных расчётов не рентабельно. Суть другого метода, метода Эйлера заключается в том, что движение жидкости подменяется изменением поля скоростей. Под полем скоростей понимают некоторую дос-таточно большую совокупность точек бесконечного пространства занятого движущейся жидкостью, когда в каждой точке пространства в каждый момент времени находится час-тица жидкости с определённой скоростью (вектором скорости). Припишем неподвижным точкам пространства скорость частиц жидкости, которые в данный момент времени нахо-дятся в этих точках. Поскольку пространство бесконечно и непрерывно, то мы имеем мас-сив данных о скоростях достаточно полный, чтобы определить (задать) поле в каждой его точке. Условно, нос достаточной точностью такое поле можно считать непрерывным. Несмотря на то, что исходные условия создания модели движущийся жидкости до-вольно сложные, тем не менее, метод Эйлера весьма удобен для расчётов. Построение поля скоростей осуществляет-ся следующим образом: На некоторый момент времени (например, to
)
произвольным образом выберем необходимое число точек, в которых находятся частицы жид-кости. Приписав их скорости ![]() точкам неподвижного про-странства (1, 2, 3, 4, 5 и 6) мы сделаем «момен-тальную фотографию» поля скоростей на вы-бранный момент времени. В следующий момент времени
точкам неподвижного про-странства (1, 2, 3, 4, 5 и 6) мы сделаем «момен-тальную фотографию» поля скоростей на вы-бранный момент времени. В следующий момент времени ![]() в тех же выбранных точках неподвижного пространства будут находиться другие частицы жидкости, имеющие другие ско-рости . Выполнив уже известную процедуру второй раз, получим но-
в тех же выбранных точках неподвижного пространства будут находиться другие частицы жидкости, имеющие другие ско-рости . Выполнив уже известную процедуру второй раз, получим но-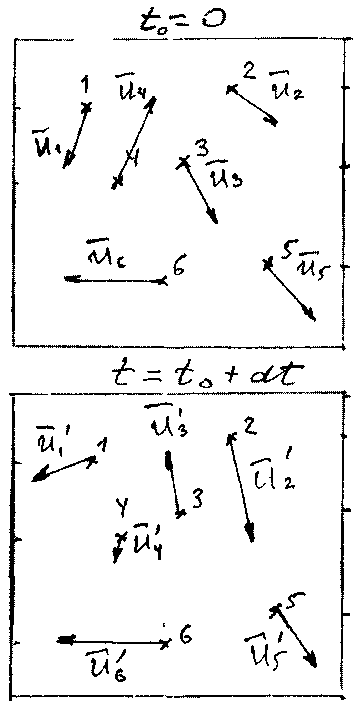 вую «моментальную фотографию» поля скоро-стей на момент времени
вую «моментальную фотографию» поля скоро-стей на момент времени![]() . Теперь вместо изучения траекторий частиц жидкости будем сравнивать поля скоростей. Тогда система уравнений примет вид:
. Теперь вместо изучения траекторий частиц жидкости будем сравнивать поля скоростей. Тогда система уравнений примет вид:
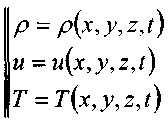
Поле скоростей движения жидкости иногда называют гидродинамическим полем по аналогии с электромагнитным, тепловым и др. полями. Это определение не противоречит физической стороне процесса движения жидкости. Анализируя состояние гидродинами-ческого поля на разные моменты времени, можно отметить, что с течени-ем времени поле изменилось, несмотря на то, что в отдельных точках 5 и 6 скорости оста-лись постоянными![]() Такое поле называют нестационарным гидродина-мическим полем. В частном случае, когда во всех точках неподвижного пространства с течением времени предыдущие частицы жидкости сменяются другими с такими же скоро-стями, то поле скоростей во времени не меняется. Такое гидродинамическое поле называ-ют стационарным. В соответствии с этим различают и два вида движения жидкости: уста-новившееся, когда поле скоростей является стационарным и неустановившееся при неста-ционарном гидродинамическом поле. 3.2.Кинематические элементы движущейся жидкости
Основной кинематической характеристикой гидродинамического поля является ли-ния тока - кривая, в каждой точке которой вектор скорости направлен по касательной к кривой. И ходя из данного определения можно записать дифференциальное уравнение линии
Такое поле называют нестационарным гидродина-мическим полем. В частном случае, когда во всех точках неподвижного пространства с течением времени предыдущие частицы жидкости сменяются другими с такими же скоро-стями, то поле скоростей во времени не меняется. Такое гидродинамическое поле называ-ют стационарным. В соответствии с этим различают и два вида движения жидкости: уста-новившееся, когда поле скоростей является стационарным и неустановившееся при неста-ционарном гидродинамическом поле. 3.2.Кинематические элементы движущейся жидкости
Основной кинематической характеристикой гидродинамического поля является ли-ния тока - кривая, в каждой точке которой вектор скорости направлен по касательной к кривой. И ходя из данного определения можно записать дифференциальное уравнение линии  тока:
тока: 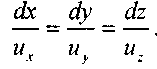 Если через некоторую неподвижную в пространстве кривую провести линии тока, то полученная поверхность называется поверхностью тока, а образованное этой поверхно-стью тело будет называться трубкой тока. Жидкость, на-полняющая трубку тока, называется элементарной струйкой. Поскольку линии тока никогда не пересекают-ся, то поверхность трубки тока является непроницаемой
Если через некоторую неподвижную в пространстве кривую провести линии тока, то полученная поверхность называется поверхностью тока, а образованное этой поверхно-стью тело будет называться трубкой тока. Жидкость, на-полняющая трубку тока, называется элементарной струйкой. Поскольку линии тока никогда не пересекают-ся, то поверхность трубки тока является непроницаемой 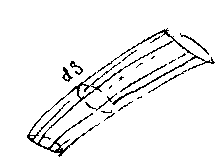 внешней границей для элементарной струйки жидкости. Сечение трубки тока, нормальное к линиям тока называется живым сечением элементар-ной струйки dS
.
При установившемся движении жидкости понятия линии тока и траекто-рии движения частицы жидкости совпадают. Объём жидкости протекающий через живое сечение элементарной струйки в единицу времени называется расходом элементарной струйки.
внешней границей для элементарной струйки жидкости. Сечение трубки тока, нормальное к линиям тока называется живым сечением элементар-ной струйки dS
.
При установившемся движении жидкости понятия линии тока и траекто-рии движения частицы жидкости совпадают. Объём жидкости протекающий через живое сечение элементарной струйки в единицу времени называется расходом элементарной струйки. 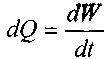 ? где: объём жидкости, протекающий через живое сечение трубки тока за время расход жидкости в живом сечении трубки тока. Размерность расхода жидкости в системе СИ -м/с.
Гидродинамическое поле считается потенциальным (безвихревым), если в этом поле отсутствует вихревое движение жидкости. В потенциальном поле может существовать лишь поступательное или криволинейное движение жидкости. 3.3 Уравнение неразрывности жидкости
Если в гидродинамическом поле отсутствуют вихри, то; для такого поля можно за-писать уравнение, связывающее параметры движущейся жидкости (плотность жидкости) с параметрами, характеризующими условия движения жидкости. Вывод такого уравне-ния основан на представлении жидкости как сплошной непрерывной среды, в силу чего такое уравнение получило название уравнения неразрывности. Для этой цели выделим в пространст-ве малый элемент жидкой среды в виде па-
? где: объём жидкости, протекающий через живое сечение трубки тока за время расход жидкости в живом сечении трубки тока. Размерность расхода жидкости в системе СИ -м/с.
Гидродинамическое поле считается потенциальным (безвихревым), если в этом поле отсутствует вихревое движение жидкости. В потенциальном поле может существовать лишь поступательное или криволинейное движение жидкости. 3.3 Уравнение неразрывности жидкости
Если в гидродинамическом поле отсутствуют вихри, то; для такого поля можно за-писать уравнение, связывающее параметры движущейся жидкости (плотность жидкости) с параметрами, характеризующими условия движения жидкости. Вывод такого уравне-ния основан на представлении жидкости как сплошной непрерывной среды, в силу чего такое уравнение получило название уравнения неразрывности. Для этой цели выделим в пространст-ве малый элемент жидкой среды в виде па-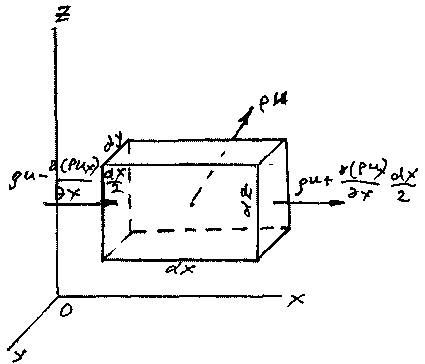 раллелепипеда, стороны которого будут равны соответственно.
раллелепипеда, стороны которого будут равны соответственно.![]() . Грани параллелепипеда пусть будут параллельны координатным плоскостям. В центре элемента в данный момент времени будет находиться частица жидкости, плотность которой равна р,
а вектор скорости движения и
направлен таким образом, что жидкость втекает внутрь элемента через левую, нижнюю и переднюю грани элемента и вытекает через противопо-ложные грани. Будем считать также, что размер элемента достаточно мал, и можно допус-тить, что в пределах этого элемента изменение плотности жидкости и скорости её движе-ния будет прямо пропорционально расстоянию от центра элемента. Одновременно разме-ры граней будут достаточно велики по сравнению с точкой, что позволит утверждать, что плотность жидкости и скорость во всех точках граней будут одинаковыми, как и плот-ность жидкости в пределах соответствующих граней. Тогда произведение плотности жид-кости на вектор скорости (импульс) в специальной литературе часто называют вектором массовой скорости ри.
В таком случае проекция вектора массовой скорости в центре левой грани элемента на ось ОХ
будет равна:
. Грани параллелепипеда пусть будут параллельны координатным плоскостям. В центре элемента в данный момент времени будет находиться частица жидкости, плотность которой равна р,
а вектор скорости движения и
направлен таким образом, что жидкость втекает внутрь элемента через левую, нижнюю и переднюю грани элемента и вытекает через противопо-ложные грани. Будем считать также, что размер элемента достаточно мал, и можно допус-тить, что в пределах этого элемента изменение плотности жидкости и скорости её движе-ния будет прямо пропорционально расстоянию от центра элемента. Одновременно разме-ры граней будут достаточно велики по сравнению с точкой, что позволит утверждать, что плотность жидкости и скорость во всех точках граней будут одинаковыми, как и плот-ность жидкости в пределах соответствующих граней. Тогда произведение плотности жид-кости на вектор скорости (импульс) в специальной литературе часто называют вектором массовой скорости ри.
В таком случае проекция вектора массовой скорости в центре левой грани элемента на ось ОХ
будет равна: 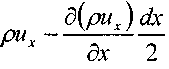 а проекция вектора массовой скорости в центре правой грани элемента на ось ОХ:
&
Масса жидкости, поступившая через левую грань элемента за малый интервал времени dt
\
а проекция вектора массовой скорости в центре правой грани элемента на ось ОХ:
&
Масса жидкости, поступившая через левую грань элемента за малый интервал времени dt
\
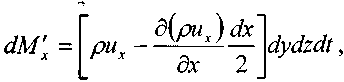 масса жидкости, вытекшая через правую грань элемента за малый интервал времени dt
:
масса жидкости, вытекшая через правую грань элемента за малый интервал времени dt
:
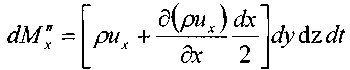 Изменение массы жидкости внутри элемента при движении жидкости вдоль оси ОХ:
Аналогично, изменение массы жидкости внутри элемента при движении жидкости вдоль оси OY
:
1,
Изменение массы жидкости внутри элемента при движении жидкости вдоль оси ОХ:
Аналогично, изменение массы жидкости внутри элемента при движении жидкости вдоль оси OY
:
1, 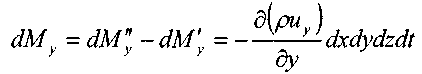 и вдоль оси OZ:
Окончательно, изменение массы жидкости внутри элемента при движении жидкости в произвольном направлении: ? или
и вдоль оси OZ:
Окончательно, изменение массы жидкости внутри элемента при движении жидкости в произвольном направлении: ? или 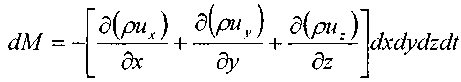 Величина плотности жидкости в начальный момент (до начала движения жидкости t
=
Q
) -
р, а по истечении бесконечно малого интервала времени (т.е.
Величина плотности жидкости в начальный момент (до начала движения жидкости t
=
Q
) -
р, а по истечении бесконечно малого интервала времени (т.е.![]()
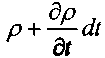
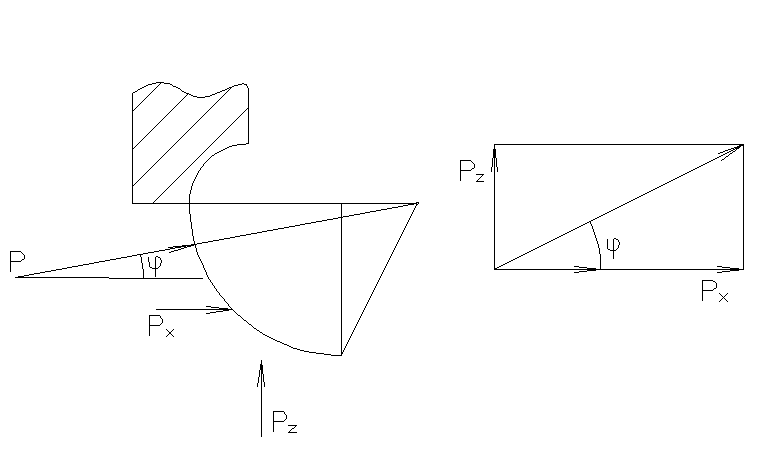
Сила F давления жидкости на криволинейные, например цилиндрические, поверхности АВ (рис.6) складывается из горизонтальной F Г и вертикальной F В составляющих и определяется их геометрической суммой
Каждая из составляющих силы F находится отдельно.
Горизонтальная составляющая
Горизонтальная составляющая F Г силы, действующей на криволинейную поверхность, равна силе давления P жидкости на плоскую вертикальную прямоугольную фигуру А 1 В 1 , которая представляет собой проекцию криволинейной стенки АВ на вертикальную плоскость (рис.7)
где p c - давление в центре тяжести (т.С) вертикальной проекции, Па;
Расчет вертикальной составляющей требует проведения дополнительных построений, для определения т.наз. тела давления . Тело давления - это фигура, которая всегда находится над криволинейной поверхностью АВ (рис.8) и ограничена самой этой поверхностью, плоскостью свободной поверхности жидкости (ОА) и вертикальными плоскостями, проходящими через границы криволинейной стенки (ОВ). Тело давления ОАВ показано штриховкой.
На рис.8,а тело давления находится в области, реально занятой жидкостью, в отличие от тела давления на рис.8,б. В первом случае тело давления называется положительным (действительным), во втором случае – отрицательным (мнимым).
Вертикальная составляющая F В силы, действующей на криволинейную поверхность АВ, по величине равна силе тяжести G тела давления. При этом, для положительного тела давления (рис.8,а) она направлена вниз, т.е. равна силе тяжести со знаком плюс (F B =+G ), а для отрицательного (рис.8,б) направлена вверх (F B =-G ) Линия действия F В проходит через центр тяжести (цт) тела давления.
Например, для криволинейной стенки АВ, которая представляет собой круглоцилиндрическую поверхность с радиусом кривизны r =H , тело давления представляет собой четверть цилиндра (рис.9), и тогда вертикальная составляющая будет равна
где V тд . - объем тела давления, м 3 .
В этом случае вертикальная составляющая F B направлена вниз, так как жидкость находится над стенкой и заполняет тело давления.
Стенка может иметь сложную форму, когда отдельные части ее поверхности оказываются одновременно как над жидкостью, так и под ней, как например, на рис.11. В этом случае всю криволинейную поверхность АВС следует разделить на частные поверхности АВ и ВС с разным по знаку наклоном. Для каждой из них в отдельности строятся тела давления, вертикальные составляющие которых (F B ’ и F B ”) действуют в противоположных направлениях. После их суммирования получают результирующее тело давления ABC, сила тяжести которого равна вертикальной составляющей силы давления на поверхность ABC.
Если жидкость находится по обе стороны криволинейной стенки, то тела давления от двух слоев жидкости строятся отдельно и затем определяется их геометрическая сумма.
Линия действия равнодействующей силы давления на круглоцилиндрические поверхности всегда направлена по радиусу и проходит через их геометрическую ось О (рис.9, 10). Угол наклона вектора этой силы к горизонту вычисляют по формуле
1.6. Контрольные задания по разделу "Свойства жидкости и газа. Гидростатика"
Определить абсолютное и избыточное (или вакуум) давление в т.А (рис.12) и одну из пропущенных величин в таблице 1, если остальные величины заданы. Налитые в резервуары жидкости с плотностями r 1 и r 2 не смешиваются и находятся в состоянии покоя. Значение давления дано в атмосферах, p A = 1атм =101325Па.
Таблица 1
| № вар | p 1 , атм | p 2 , атм | h 1 , м | h 2 , м | h 3 , м | h 4 , м | h 5 , м | r 1, кг/м 3 | r 2 , кг/м 3 |
| p А | p абс =1,3 | ? | |||||||
| p изб =0,2 | p А | ? | |||||||
| p абс =1,5 | p А | ? | |||||||
| p абс =0,5 | p А | ? | |||||||
| ? | p А | ||||||||
| p абс =0,3 | ? | ||||||||
| № вар | p 1 , атм | p 2 , атм | h 1 , м | h 2 , м | h 3 , м | h 4 , м | h 5 , м | r 1, кг/м 3 | r 2 , кг/м 3 |
| p изб =0,2 | p вак =0,1 | ? | |||||||
| p абс =1,2 | p изб =0,3 | ? | |||||||
| p А | p абс =1,2 | ? | |||||||
| p вак =0,2 | p абс =0,9 | ? |
По данным таблицы 2 определить равнодействующую сил избыточного давления на 1 погонный метр (нормально к плоскости чертежа) поверхности ABC. Найти угол наклона линии действия сил избыточного давления воды на поверхность ABC слева. В расчетах принять h =2м, r =1м.
Таблица 2
| № варианта | Форма поверхности АВС |
ОСНОВЫ ГИДРОДИНАМИКИ
В этом разделе следует изучить основные гидравлические параметры потока жидкости, виды и режимы ее движения. Необходимо знать математическое выражение основных законов классической физики - законов сохранения вещества и энергии - применительно к движению жидкостей и газов.
Решение многих практических задач, основано на использовании уравнений Бернулли и неразрывности потока (сохранение расхода по длине трубы). Поэтому очень важным является изучение этих уравнений и следствий из них.
При решении некоторых простейших задач о движении жидкостей часто в первом приближении делают допущение о том, что движущаяся жидкость является идеальной . Под идеальной понимают жидкость абсолютно несжимаемую и нерасширяемую, не способную сопротивляться растяжению и сдвигу. Главное, чем отличается идеальная жидкость от жидкости реальной, - это отсутствие вязкости, которая вызывает способность сопротивляться сдвигу, т.е. возникновению касательных напряжений (трения в жидкости). Следовательно, в движущейся идеальной жидкости возможен лишь один вид напряжений – напряжение сжатия, т.е. давление p , а касательное напряжение τ =0.
Основными уравнениями, позволяющими решать простейшие задачи о движении идеальной жидкости являются уравнение постоянства расхода (уравнение неразрывности) и уравнение Бернулли.
Давление, созданное в жидкости, действуя на поверхности различных устройств и их элементов, создает силу. Плоскими поверхностями могут быть стенки различных резервуаров, тела плотин, клапаны, щиты и затворы.
Определим величину силы, действующей на плоскую поверхность, и точку ее приложения.
Представим (рис.3.15) сосуд, наполненный жидкостью и имеющий плоскую стенку ОМ под углом α к горизонту. В плоскости этой стенки наметим оси координат ОУ и ОХ. Ось ОХ направим перпендикулярно к плоскости чертежа.
На стенке сосуда наметим некоторую плоскую фигуру АВ любого очертания, имеющую площадь w. Из точки О проведем ось ОХ, нормальную к направлению АВ, т.е. ось ОХ совместим с плоскостью чертежа. Будем мысленно вращать фигуру АВ вокруг оси ОУ так, чтобы эта фигура совместилась с плоскостью чертежа.
Выделим на площади фигуры бесконечно малую поверхность в виде полоски dw, погруженную на глубину h. При этом расстояние полоски от оси ОХ равно y. гидростатическое давление в области бесконечно малой плоскости согласно основному уравнению гидростатики будет
Тогда сила давления на элементарную площадку
![]() . (3.16)
. (3.16)
Интегрируя выражение (3.16) в пределах площади ω и заменив h = у·sinα, получим
Интеграл представляет собой статический момент площади фигуры АВ относительно оси ОХ. Из механики известно, что
Y с w, (3.18)
где у с – расстояние центра тяжести площади фигуры АВ относительно оси ОХ.
Подставив (3.18) в (3.17) и заменив y c sinα = h c , получим силу, действующую на площадь ω:
![]() (3.19)
(3.19)
Это означает, что сила давления P жидкости на плоскую фигуру, погруженную в жидкость, равна произведению этой площади ω на гидростатическое давление в ее центре тяжести (p o +γh c).
Из формулы (3.19) следует, что сила Р состоит из двух сил: силы р о ω и силы γh с ω. Сила p о ω создает равномерную нагрузку и приложена в центре тяжести фигуры площадью ω. Сила γh с ω создает неравномерную нагрузку и поэтому точка ее приложения не совпадает с центром тяжести фигуры. Эта точка называется центром гидростатического давления; обозначается она буквой d. Для нахождения точки приложения силы γh с ω применим теорему механики о моменте равнодействующей силы: момент равнодействующей силы относительно оси ОХ равен сумме моментов от элементарных сил:
![]() . (3.20)
. (3.20)
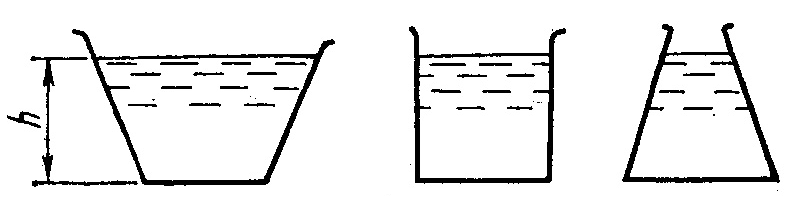
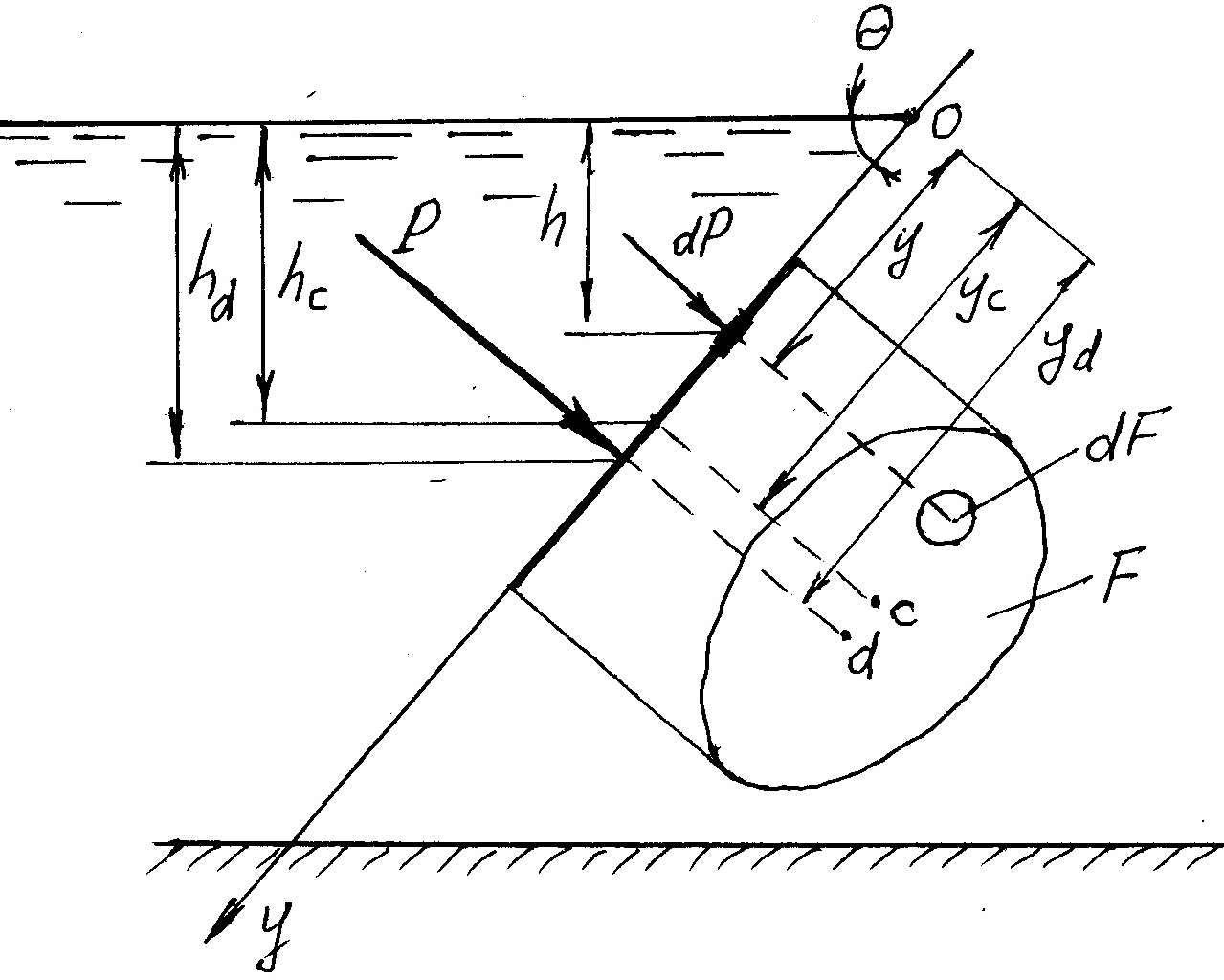
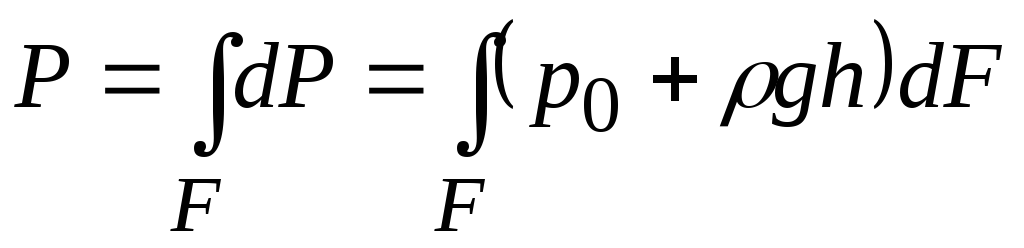
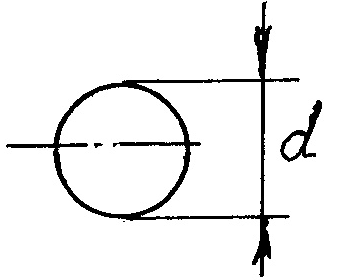
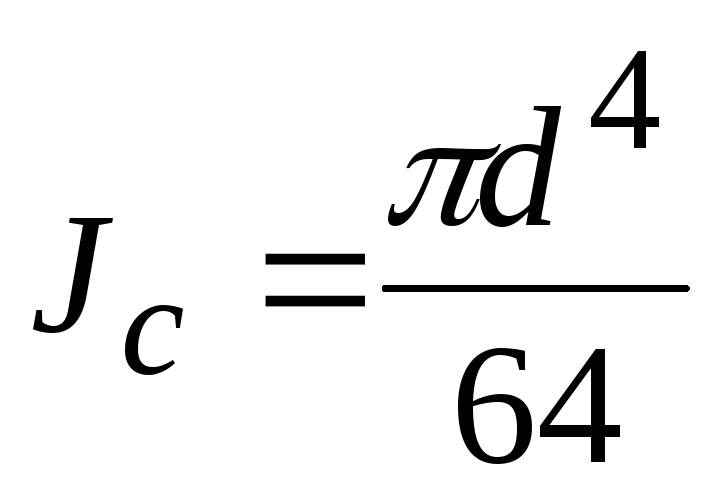
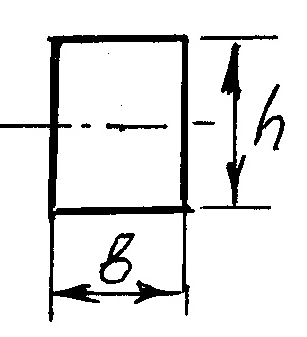
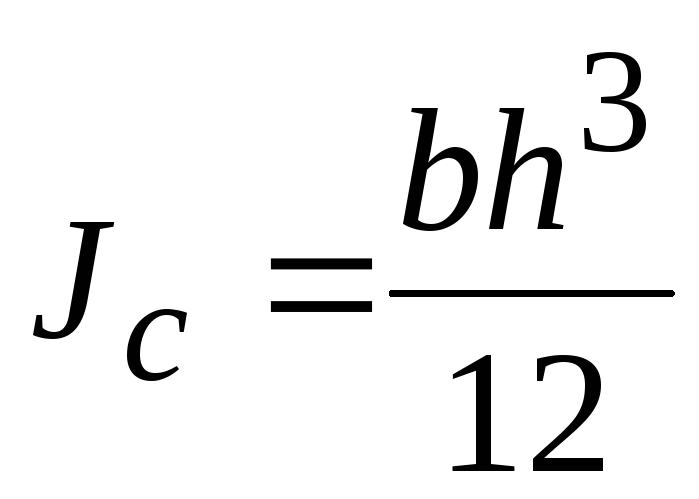
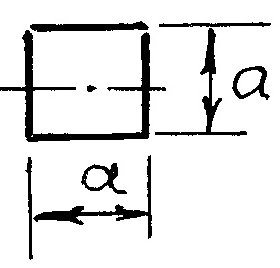
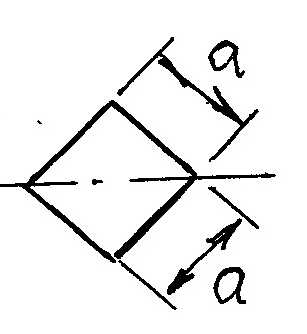
 –
сторона
–
сторона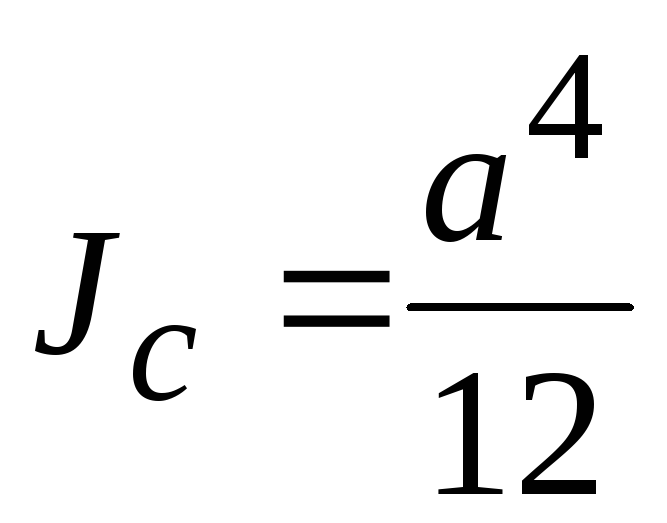
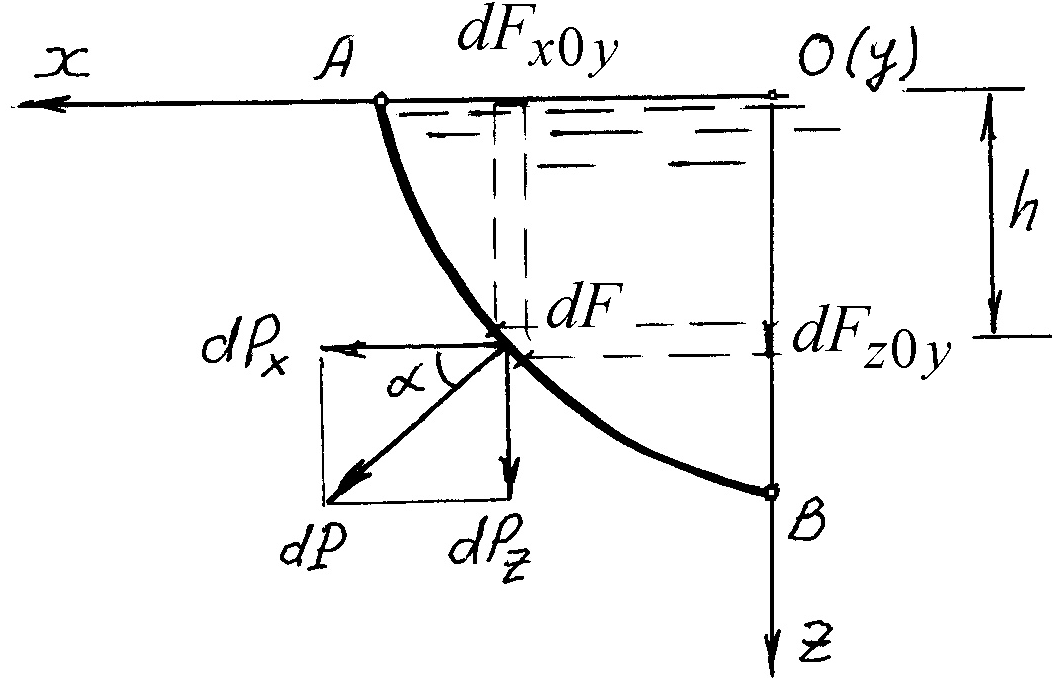
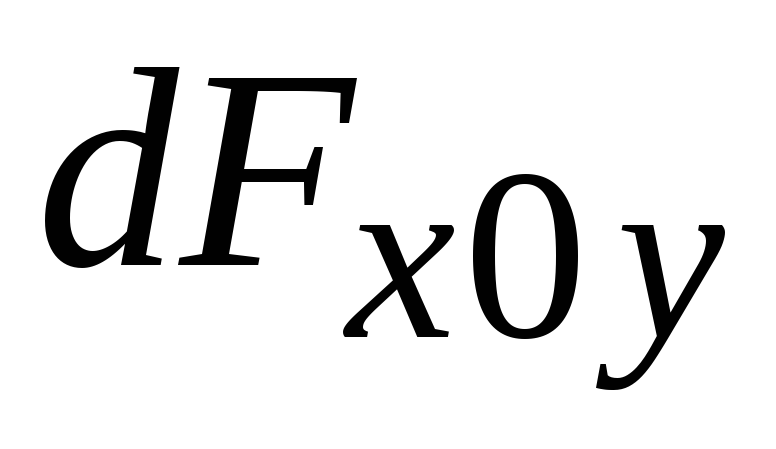 и
и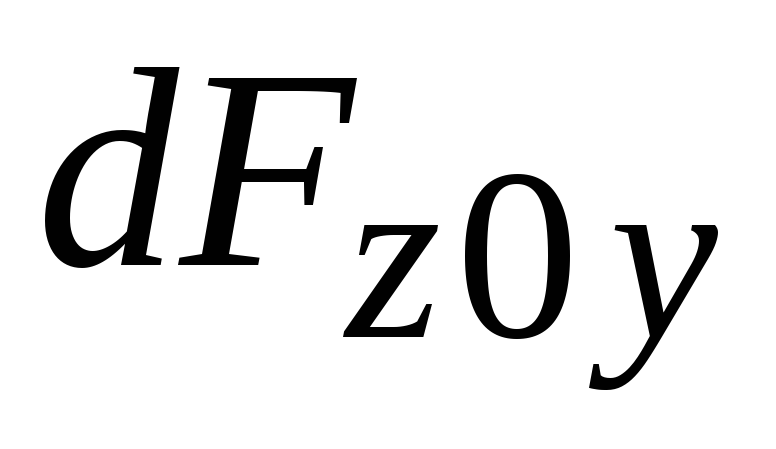 .
.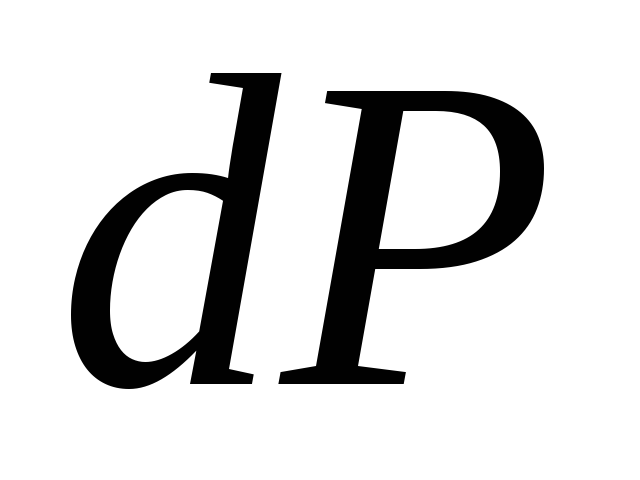 ,
ее проекции на оси
,
ее проекции на оси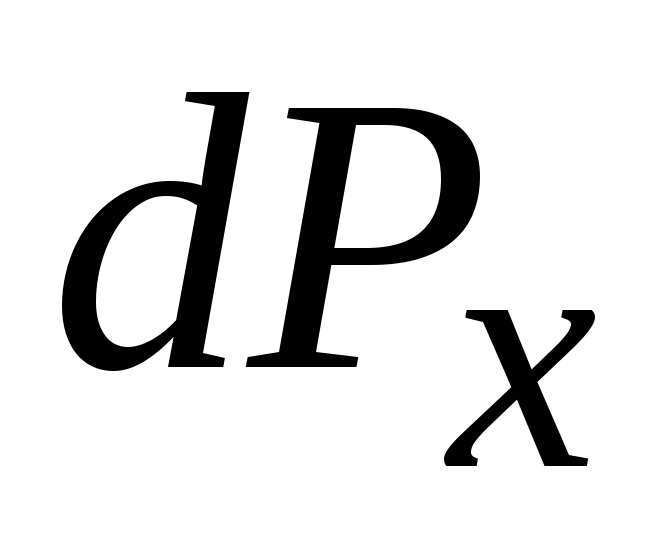 и
и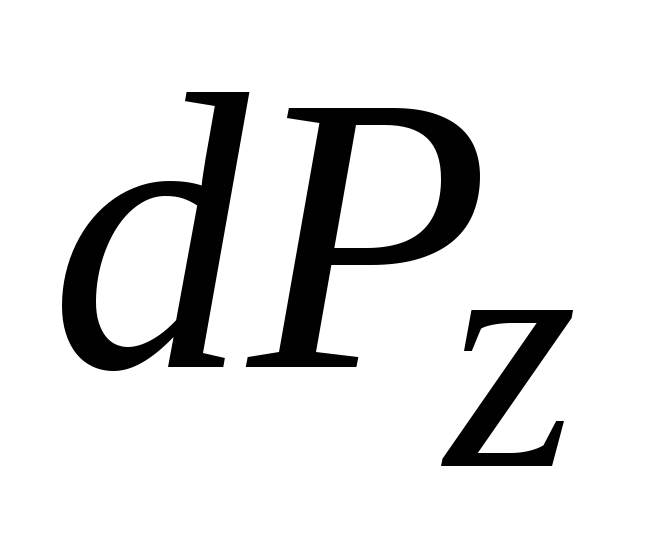 .
.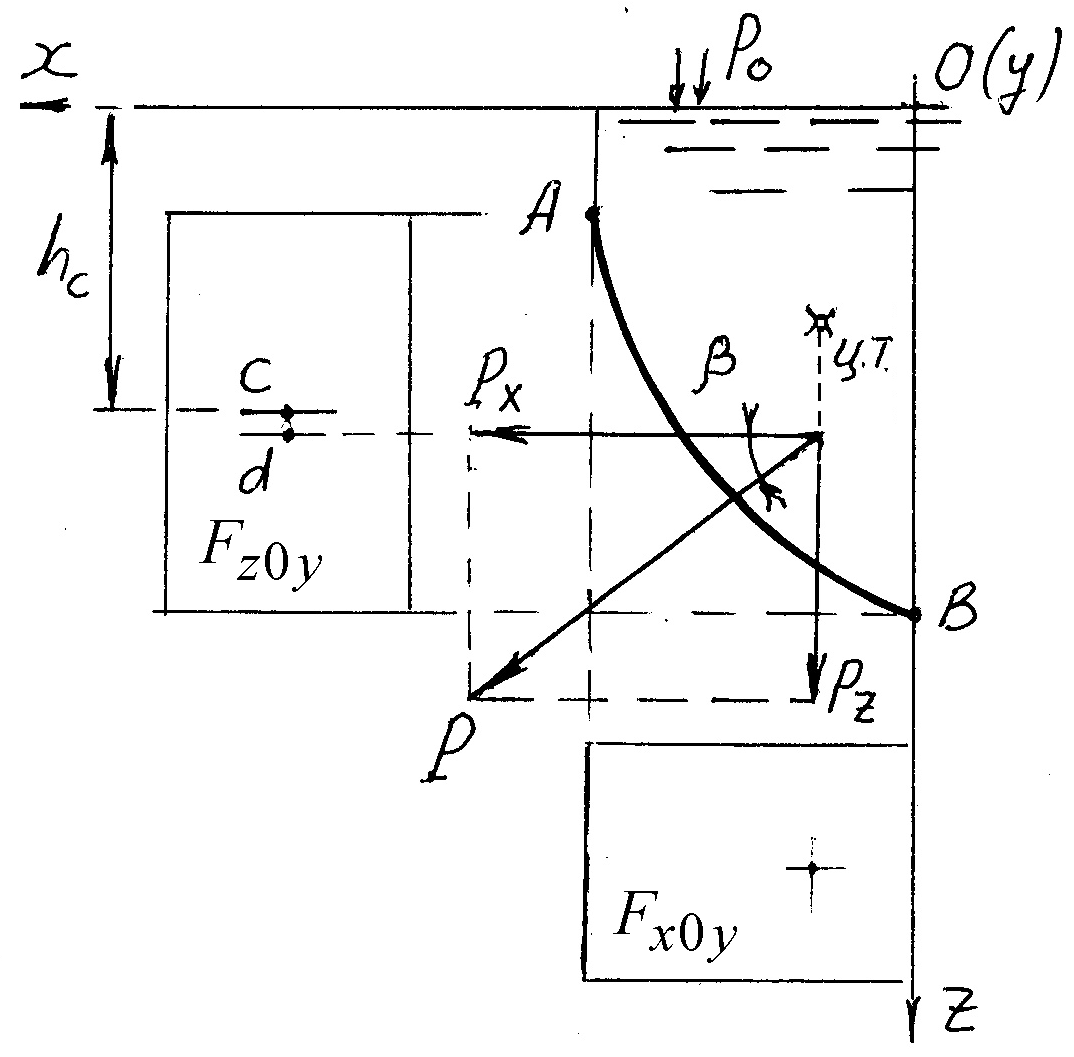
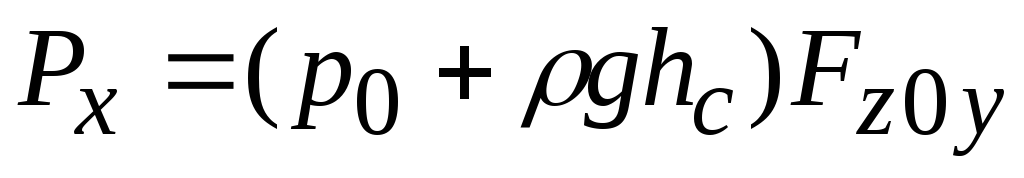
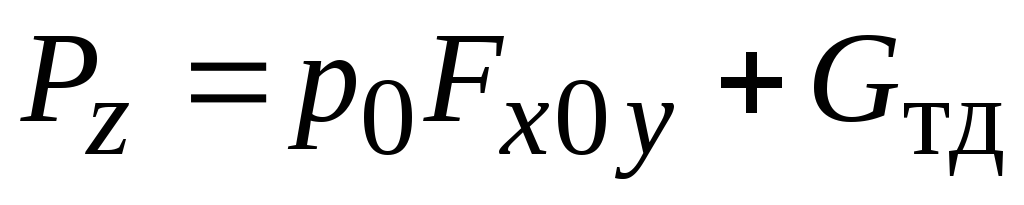
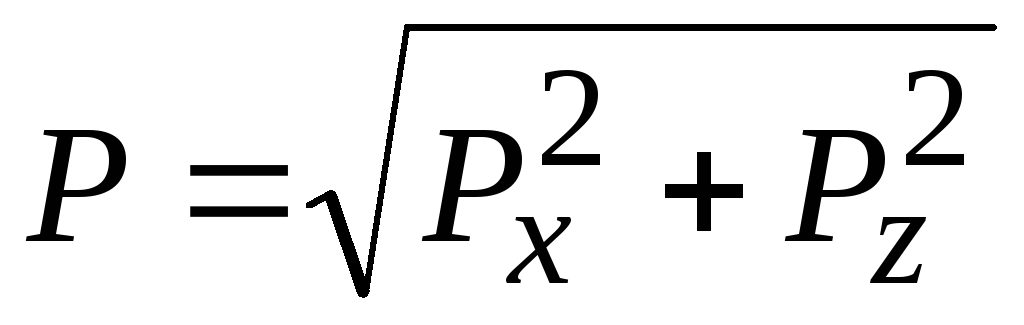
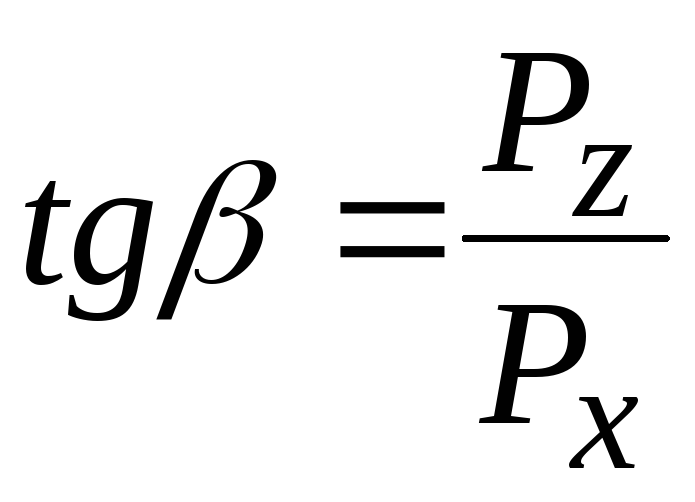
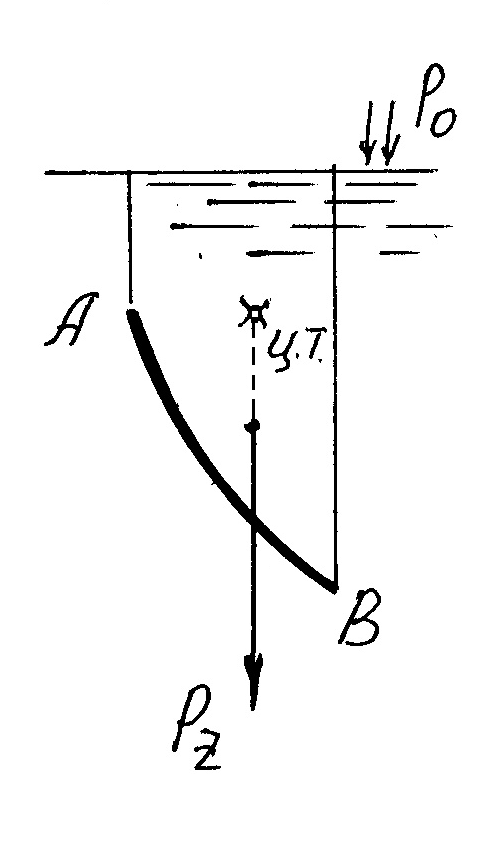
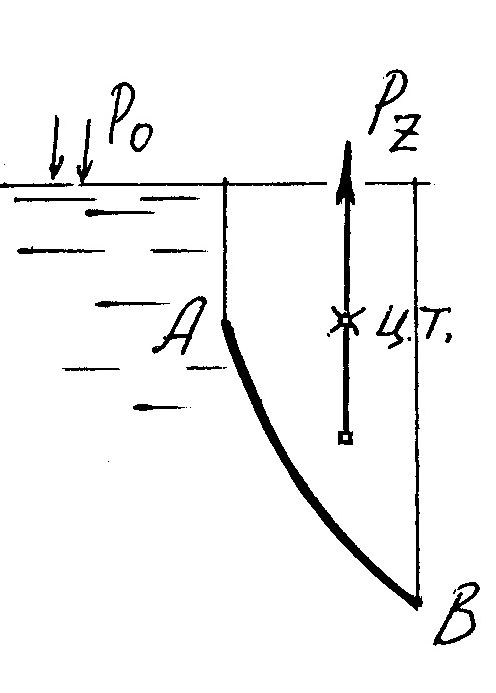
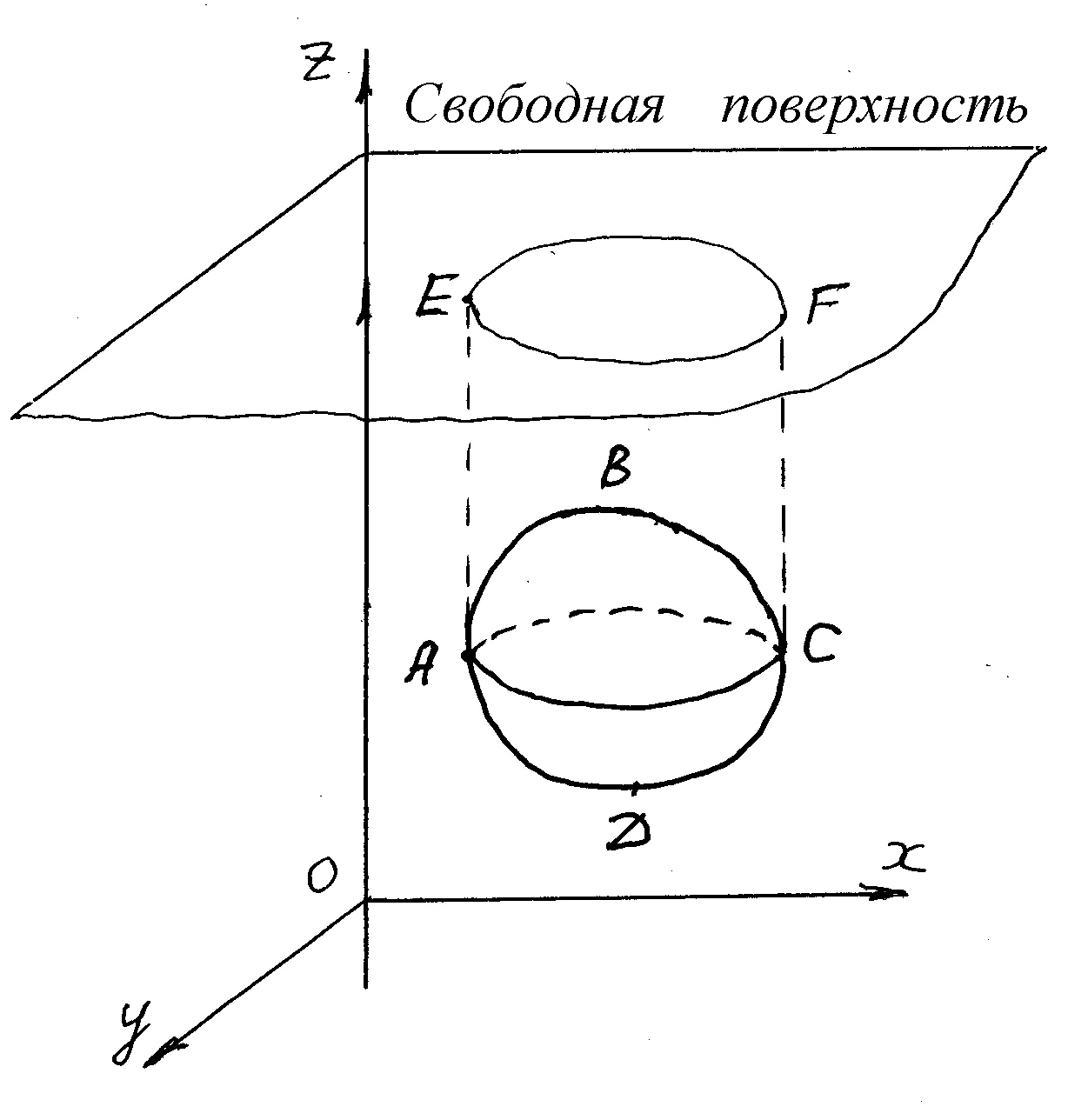
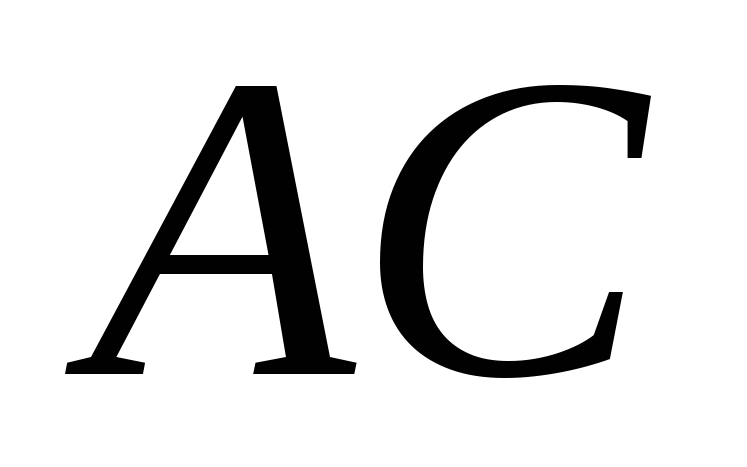 .
Сила давления на верхнюю половину
направлена вниз и равна весу жидкости
в теле давления
.
Сила давления на верхнюю половину
направлена вниз и равна весу жидкости
в теле давления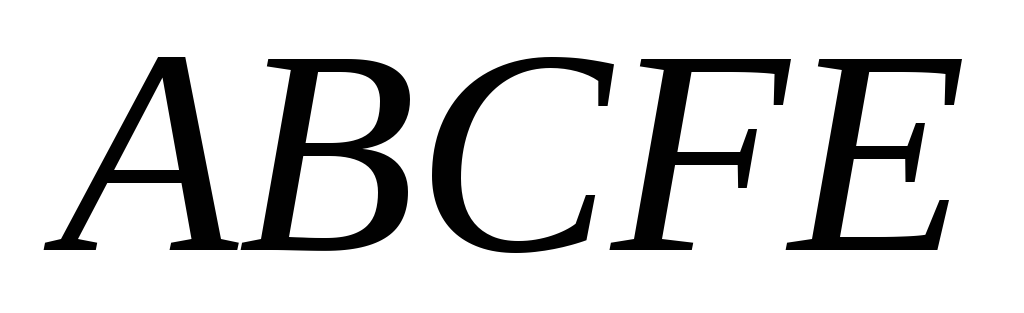 .
.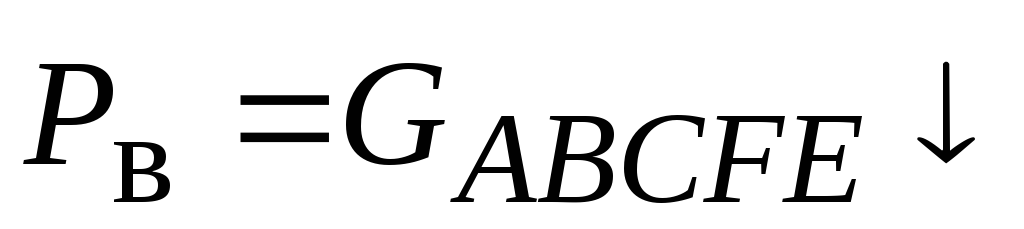
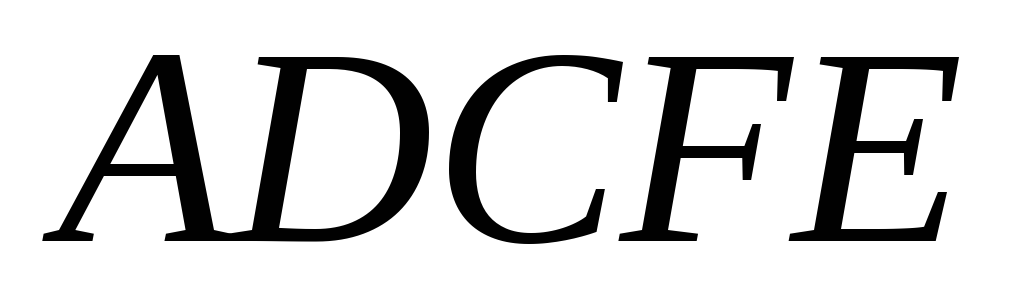 .
.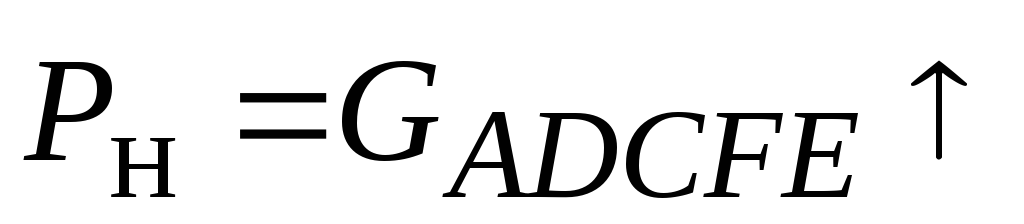
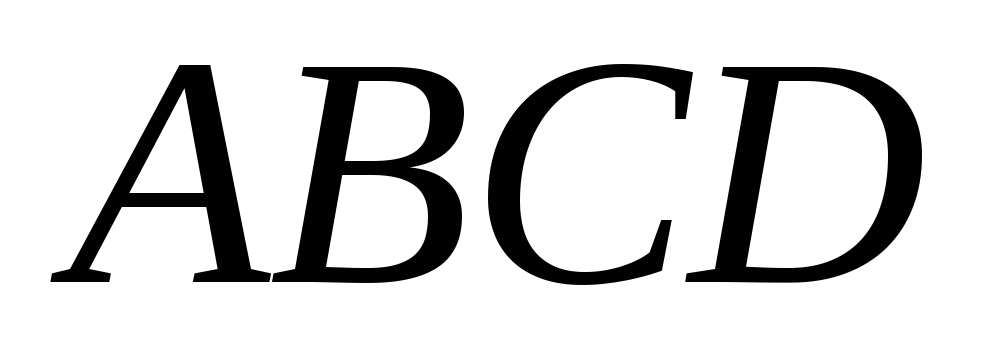 ,
ч.т.д.
,
ч.т.д.