Скорость течения газа в трубе. Движение газа по трубам. Основные положения и задачи
Лекции по гидравлике
Методы предотвращения негативных явлений гидравлического удара и его использование
Резкое увеличение давления, сопровождающее гидравлический удар - явление крайне негативное, т.к. гидравлический удар может разрушить трубопровод или какие-либо элементы гидравлических машин, испытывающие эффекты гидравлического удара. По этой причине разрабатываются методы предотвращения гидравлических ударов или уменьшить его негативное влияние. Поскольку мощность гидравлического удара напрямую зависит от массы движущийся жидкости, то для предотвращения гидравлического удара следует максимально уменьшить массу жидкости, которая будет участвовать в гидравлическом ударе. Для этого необходимо запорную арматуру монтировать в непосредственной близости к резервуару. В качестве меры уменьшения негативных последствий гидравлического удара используют замену прямого гидравлического удара на непрямой. Для этого достаточно запорную арматуру на напорных трубопроводах сделать медленно закрывающейся, что позволит уменьшить силу удара. Другой мерой борьбы с
явлением гидравлического удара является установка на напорных линиях, работающих в условиях
циклической нагрузки специальных компенсаторов с воздушной подушкой, которая принимает на себя удар
Однако в ряде случаев явление гидравлического удара успешно используется. К таким случаям использования гидравлического удара относятся производственные процессы по разрушению материалов и др. Известна специальная конструкция водоподъёмника, базирующаяся на использовании гидравлического удара.
Основной отличительной особенностью движения газа по трубам от движения капельных жидкостей заключается в том, что капельные жидкости характеризуются весьма малой сжимаемостью, а их вязкость практически не зависит от давления. По этой причине для решения большинства практических задач капельные жидкости можно считать не сжимаемыми, что позволяет значительно упростить уравнения движения такой жидкости. При движении газа таких допущений делать нельзя. Поскольку изучение общих решений уравнений газодинамики не является предметом настоящего курса, рассмотрим лишь частные задачи, встречающиеся в практике работы специалистов горных отраслей промышленности. К числу таких первоочередных задач относится изучение движения газов, включая воздух по газопроводам (воздуховодам).
Газ двигается по газопроводу при переменном давлении, т.к. давление изменяется вдоль длины газопровода из-за неизбежных потерь напора по длине трубопровода. По этой причине плотность газа и его вязкость являются величинами переменными и неодинаковы в различных сечениях газопровода. Рассмотрим наиболее простой случай газопровода (воздуховода) собранного из труб одинакового диаметра (простой газопровод S = const ) при установившемся движении газа. Тогда в соответствии с уравнением неразрывности потока газа массовый расход газа вдоль газопровода является величиной постоянной= const. При этом объёмный расход газа будет меняться от одного сечения газопровода к другому, т.к. плотность газа зависит от давления, которое по длине газопровода меняется.
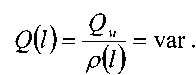
Тогда скорость движения газа также будет меняться вдоль длины газопровода:
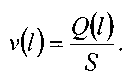
При этом должна изменяться и температура газа по длине газопровода, и, как следствие, также и вязкость газа. Однако для решения практических задач движение газа по трубопроводу можно считать изотермическим (небольшие скорости движения, теплоизоляция газопровода, небольшие перепады давления). Это допущение не приведет к серьёзным погрешностям в расчётах, но оно позволяет пренебречь изменением вязкости газа при незначительных колебаниях температуры газа в газопроводе. Т.е. полагаем, что в газопроводе соблюдается условие: Т = const и= const. При таких условиях будет посто-
янным для всего потока и число Рейнольдса, и как следствие будут одинаковым коэффициенты трения и гидравлических сопротивлений по длине потока.
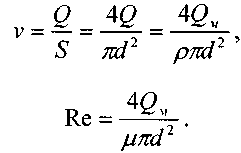
Отметим, что в последнем выражении все величины, входящие в правую часть равенства являются величинами постоянными, отсюда: Re = const и /I = const. По этой причине для определения величины потерь напора и расхода газа можно воспользоваться обычным уравнением Бернулли.
10.2. Основные уравнения газодинамики для установившегося движения газа в простом газопроводе
Запишем уравнение Бернулли в дифференциальной форме:
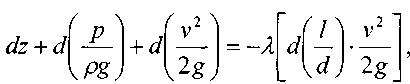
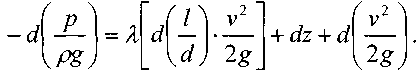
Последний член уравнения весь мал и его величиной можно пренебречь, тогда для горизонтального газопровода (z = const ) можно записать:
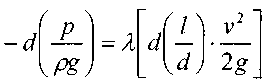
Подставив в последнее уравнение значение средней скорости движения газа, выразив её через массовый расход, получим:
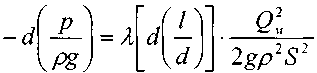
По принятым выше условиям процесс движения газа по газопроводу является изотермическим, тогда подставив в последнее уравнение значение из уравнения Бойля-Мариотта:
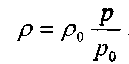 , получим:
, получим:
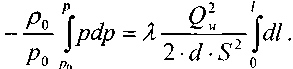
Решая последнее уравнение, получим основные расчётные формулу для определения потерь давления в газопроводе и формулу для определения массового расхода газа в газопроводе.
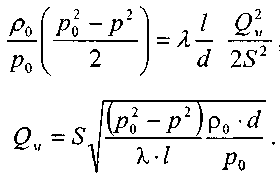 >
>
Величина коэффициента трения Л определяется по формулам для жидкости в зависимости от режима её движения или же можно воспользоваться эмпирической формулой ВННИИГаза:
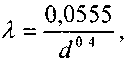 *
*
где d- диаметр газопровода в сантиметрах.
Для приближенного расчета движения жидкости или газа по трубам можно отвлечься от весьма сложных деталей этого движения (об этом будет сказано в заключительных главах) и удовольствоваться следующей упрощенной схемой. Примем поток за одномерный, т. е. будем пренебрегать изменением величины и направления скорости, а также изменениями других элементов потока (давления, плотности, температуры и др.) по сечению, перпендикулярному к оси потока; будем лишь учитывать изменение средних по сечениям величин и др. в зависимости от координаты х, определяющей положение сечения вдоль оси трубы. Площадь сечения А будем считать заданной функцией х. Отвлечемся от сил трения внутри жидкости и жидкости о стенку, а также от теплопроводности; иными словами, как повсюду в настоящей главе, будем считать жидкость идеальной.
Начнем с простейшего случая - движения несжимаемой жидкости.
В этом случае из уравнения неразрывности сразу следует
где средняя скорость в некотором начальном сечении с площадью иными словами, средняя скорость движения жидкости в любом сечении трубы обратно пропорциональна площади этого сечения.
Отсюда вытекает общеизвестное свойство движения несжимаемой жидкости по трубе переменного сечения: в сужающейся трубе жидкость движется ускоренно, в расширяющейся - замедленно.
Это очевидное свойство одномерного движения теряет свою силу при движении сжимаемого газа со сверхзвуковыми скоростями, в чем легко убедиться, составив основные уравнения одномерного стационарного движения газа:
а) уравнение Эйлера:
![]()
б) уравнение неразрывности:
![]()
Вспоминая определение местной скорости звука
перепишем уравнение Эйлера (83) в виде:
Составляя логарифмический дифференциал от обеих частей равенства (84), получим:
![]()
Исключая - из уравнений (85) и (86), найдем:
или, вводя местное число
![]()
Из этого простого уравнения вытекают важные следствия:
1. Если знак противоположен знаку т. е. при дозвуковом движении газа сохраняется то же свойство движения, что и в случае несжимаемой жидкости: с возрастанием площади сечения трубы скорость в одномерном движении уменьшается и, наоборот, при уменьшении сечения - скорость увеличивается.
2. Если знак одинаков со знаком т. е. при сверхзвуковом движении газа в сужающейся трубе движение замедляется, в расширяющейся трубе - ускоряется. Этот парадоксальный на первый взгляд результат объясняется тем, что при расширении газа плотность его настолько сильно уменьшается, что произведение в равенстве (84), несмотря на увеличение площади А, все же уменьшается и приводит к возрастанию скорости и.
3. Если Сечение трубы, в котором число достигает значения единицы, называется критическим сечением, так как в нем скорость движения и равна местной скорости звука а. Из равенства (87) следует, что критическое сечение может быть максимальным, так и минимальным по сравнению со смежными сечениями. Легко сообразить, что критическое сечение будет минимальным, так как при подходе к максимальному сечению дозвуковой поток замедляется, а сверхзвуковой ускоряется, что никак не может привести к течению со скоростью звука в критическом сечении.
Если и сечение экстремально (максимально или минимально), то по (87) либо следовательно, это сечение -
критическое, либо В последнем случае, каково бы ни было движение - дозвуковое или сверхзвуковое - скорость в экстремальном сечении принимает также экстремальное значение; при дозвуковом течении газа - минимальное в максимальном сечении и максимальное в минимальном сечении, при сверхзвуковом течении, наоборот, в максимальном сечении скорость максимальна, в минимальном - минимальна.
Переходя к более детальному изучению одномерного адиабатического и изэнтропического движения газа, заметим, что к нему применимы все ранее выведенные соотношения, связывающие между собою термодинамические параметры газа и скорость движения или число Необходимо только установить связь между одним каким-нибудь из этих параметров и сечением трубы А.
Примем за основную, например, связь между Чтобы вывести уравнение этой связи возьмем уравнение
![]()
получаемое логарифмическим дифференцированием равенства
и уравнение Бернулли в форме (47):
![]()
которое после дифференцирования дает
![]()
или, после делении обеих частей на и замены
![]()
Подставляя это значение в (88), получим
![]()
Сравнивая это уравнение с уравнением (87), будем иметь:
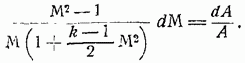
Уравнение это нетрудно проинтегрировать и получить искомое уравнение связи между числом и площадью сечения А:
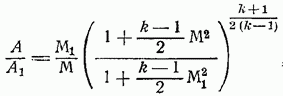
где произвольное начальное сечение трубы и число в этом сечении.
Предположим, что роль начального сечения играет критическое сечение т. е. такое сечение, в котором тогда равенство (89) приводится к более простому виду:
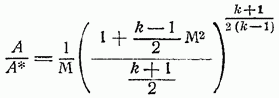
На рис. 47 приведен график этой важной зависимости для воздуха График подтверждает ранее отмеченный факт: в дозвуковом потоке для увеличения числа сечение А следует уменьшать, в сверхзвуковом потоке наоборот, увеличивать; вместе с тем график показывает количественное соотношение между изменениями чисел
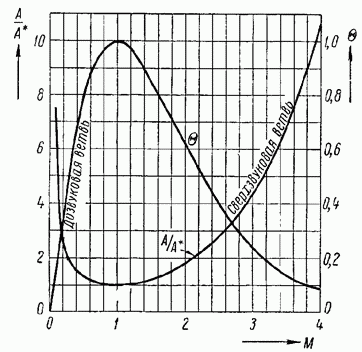
Так, например, из рис. 47 следует, что для повышения числа от 0,2 до 0,8 газ должен пройти через участок суживающейся трубы-конфузора с сечением, уменьшающимся в три раза; чтобы увеличить число от значения 1 в критическом сечении до 3,2, необходимо построить расширяющуюся трубу-диффузор - с площадью на выходе, в пять раз превышающей площадь критического сечения.
Присоединим к формуле (90) известные уже по предыдущему формулы (69), (70), (66) изэнтропической связи давления, плотности и температуры с числом которые, в силу (51) и (52) полезно
переписать в виде:
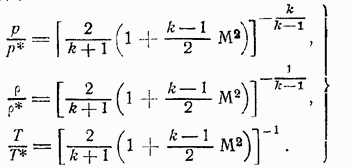
Совокупность равенств (90) и (91) представляет полное решение задачи об одномерном стационарном адиабатическом и изэнтропическом движении газа по трубе переменного сечения; решение это представлено в удобном параметрическом виде, причем роль параметра играет число Задавшись законом изменения площади сечения трубы определим по (90), а затем и искомые по (91).
Из уравнения неразрывности или сохранения массы (84) следует, что при наличии в одномерном потоке критического сечения будет существовать соотношение
![]()
где величина
![]()
представляет отношение массового расхода газа через единицу площади сечения трубы к его критическому значению. Этот безразмерный массовый расход данного газа является функцией только числа согласно (90), равен:
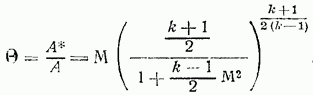
График зависимости от для воздуха приведен на том же рис. 47.
В качестве первого примера приложения выведенных формул рассмотрим классическую задачу об изэнтропическом истечении газа из резервуара (котла) очень большой вместимости.
Предположим сначала, что сопло, из которого происходит истечение, имеет вид конфузора, т. е. канала с уменьшающимся вниз по потоку сечением. Обозначим через термодинамические параметры газа в котле, где газ, в силу большой вместимости котла, может рассматриваться как покоящийся через соответствующие параметры в выходном сечении, площадь которого
пусть будет А, и через давление в среде, куда происходит истечение; это давление в теории истечения называют противодавлением.
Определим прежде всего основную характеристику одномерного потока в целом - секундный массовый расход газа одинаковый для всех сечений потока и равный
или, на основании формул (52):
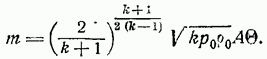
При заданных параметрах газа в котле и геометрической форме сопла секундный массовый расход газа является функцией только числа в выходном сечении, определяемой выражением в формуле (93). Что касается выходного числа то оно, в силу принятой наперед адиабатичности и изэнтропичности потока, определяется заданием давления на выходе согласно известной формуле (69):
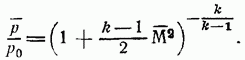
Определяя отсюда в функции от и подставляя это значение в выражение в, получим после простых приведений формулу:
представляющую, очевидно, простое приложение ранее указанной формулы Сен-Венана и Ванцеля [(67) гл. III].
Пользуясь одновременно формулами (94) и (95), легко исследовать изменение секундного массового расхода истечения в функции отпротиводавления которое при совпадает практически с или числа в выходном сечении.
При движении газа на каждый его объем будут действовать не только те силы, которые характерны для статики, но и другие, сильно усложняющие как явление в целом, так и его математическое описание. Для движения идеального газа этими дополнительными силами будут силы инерции, а для реального газа - силы инерции и трения (вязкости). В механике сплошных сред большое внимание уделяется выводу и использованию соответствующих математических уравнений, описывающих движение идеальных (уравнения Эйлера) и реальных сред (уравнения Навье - Стокса). Уравнения Навье - Стокса настолько сложны, что к настоящему времени решены лишь для крайне ограниченного числа случаев. Эта сложность вызвана сильным влиянием вязкости среды на различные аспекты процесса движения. В силу этого в допустимых случаях прибегают к решению уравнений Эйлера для движения идеальных сред с введением необходимых поправок и уточнений. Таким образом, получено одно из важнейших уравнений гидро- и аэродинамики - уравнение (закон) Бернулли.
Уравнение Бернулли.
В практических условиях распространенным является движение в трубах и каналах, когда газ через боковые стенки не расходуется. В таких случаях для расчетов применяется уравнение Бернулли, полученное для струйки тока (трубка тока), характерной тем, что расход газа в любом ее сечении остается неизменным (обмен газом между всем потоком и струйкой тока через ее боковые границы отсутствует).
Для несжимаемого газа () уравнение Бернулли при условии, что все его члены отнесены к единице объема, имеет вид
В
соответствии с этим величина 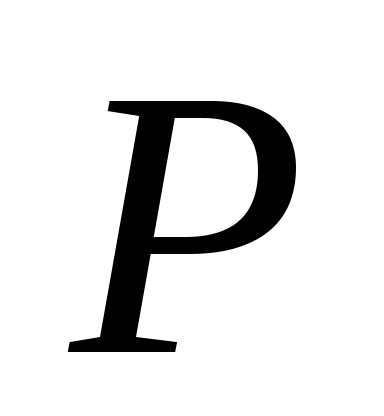 является пьезометрическим
давлением, величина
является пьезометрическим
давлением, величина 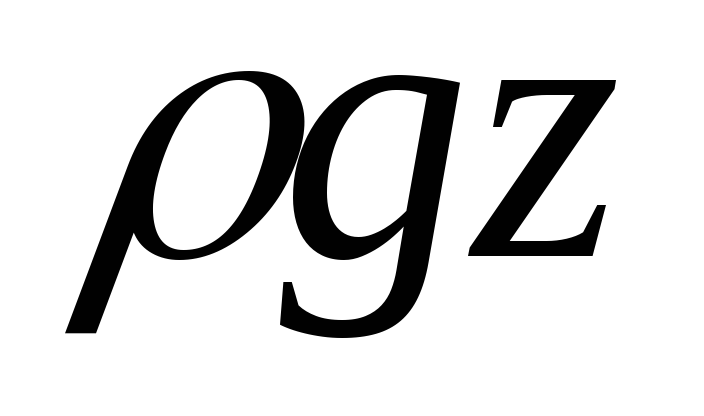 -
геометрическим давлением, величина
-
геометрическим давлением, величина 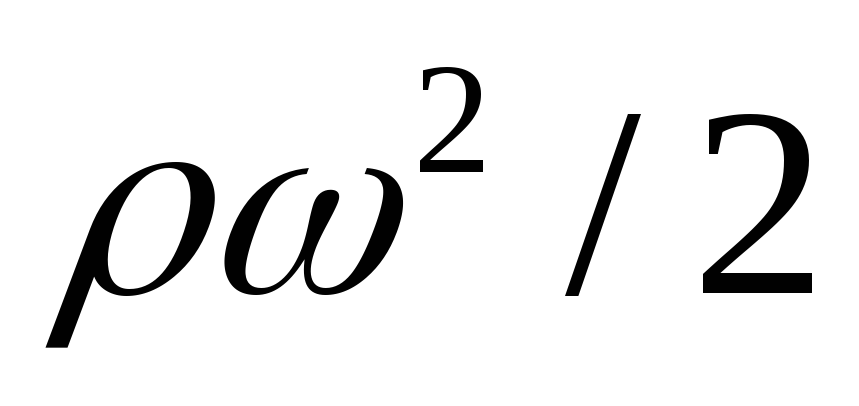 - скоростным давлением.
- скоростным давлением.
Уравнение
Бернулли представляет собой закон
сохранения
энергии, поскольку сумма 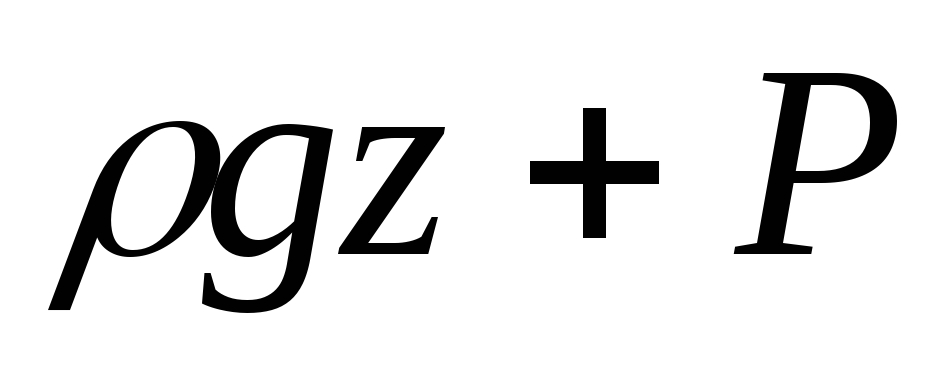 характеризует
потенциальную, а
величина
характеризует
потенциальную, а
величина 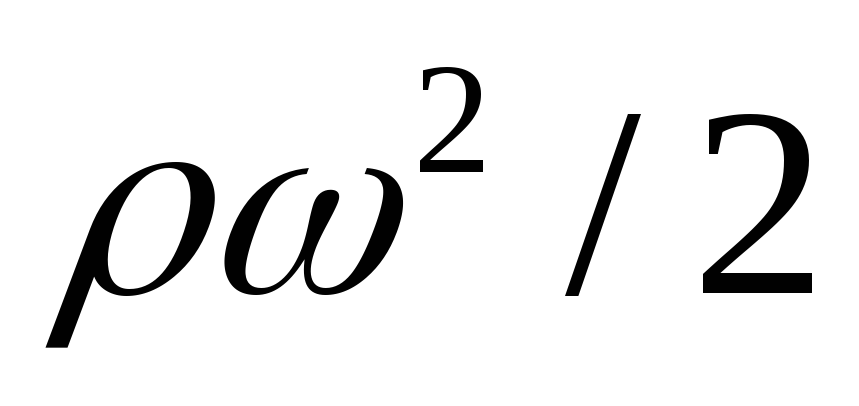 -
кинетическую энергию.
-
кинетическую энергию.
В
металлургической теплотехнике
в большинстве случаев пользуются
давлением, избыточным
над атмосферным. Необходимо уравнение
Бернулли привести к такому виду, при
котором все члены
его были бы выражены в избыточных
давлениях. Для
этого представим себе канал, окруженный
воздухом плотностью
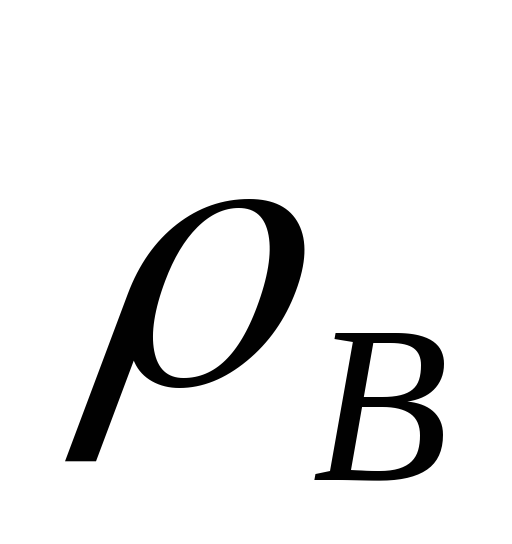 ,
по которому движется газ плотностью
,
по которому движется газ плотностью 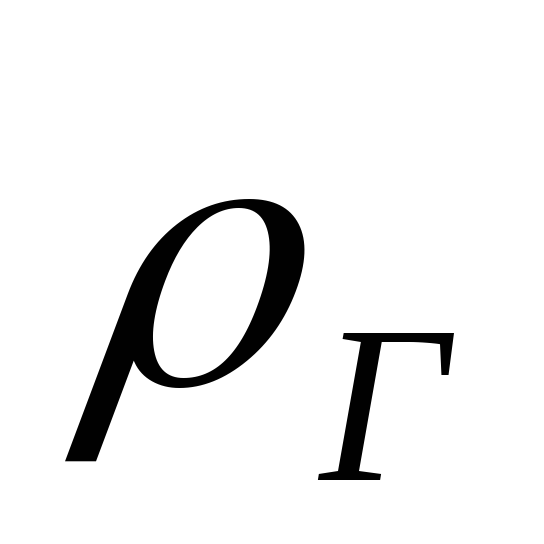 .
Принимая
плотности газа и воздуха неизменными,
напишем
уравнение Бернулли и для газа и воздуха
применительно к
сечениям канала
.
Принимая
плотности газа и воздуха неизменными,
напишем
уравнение Бернулли и для газа и воздуха
применительно к
сечениям канала 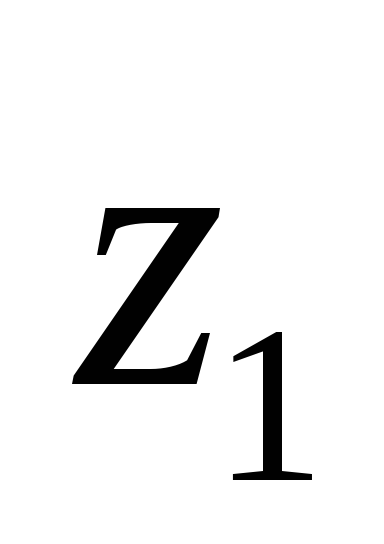 и
и 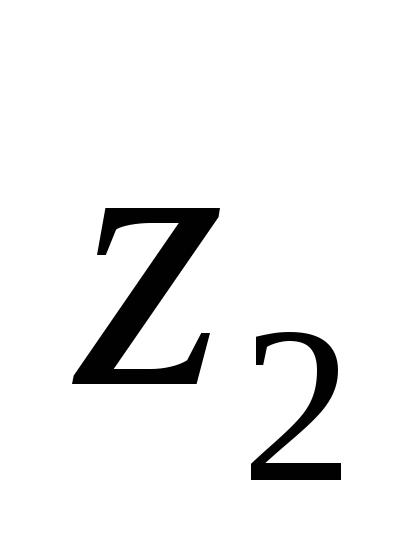 .
.
Уравнение для газа
Уравнение для воздуха (считаем, что воздух находится в спокойном состоянии)
Вычитая из первого второе, получаем уравнение Бернулли для газа в избыточных давлениях:
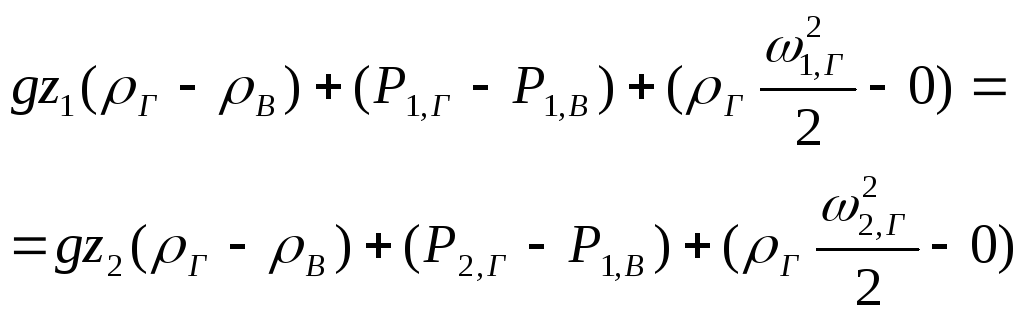 .
(11)
.
(11)
Уравнение можно переписать в таком виде:
Однако
равенство 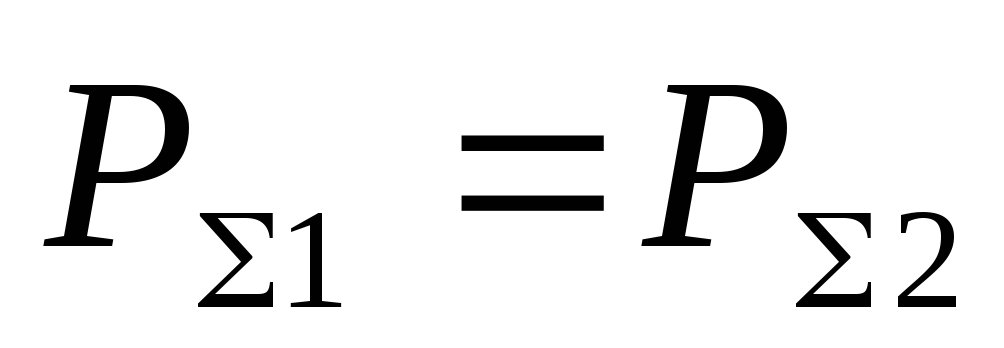 строго
справедливо лишь для
идеальной среды, полностью лишенной
вязкости. Если
по каналу перемещается реальная (вязкая)
жидкость
(газ), то часть энергии тратится на
преодоление трения и различных
сопротивлений и происходит потеря
энергии.
строго
справедливо лишь для
идеальной среды, полностью лишенной
вязкости. Если
по каналу перемещается реальная (вязкая)
жидкость
(газ), то часть энергии тратится на
преодоление трения и различных
сопротивлений и происходит потеря
энергии.
В этом
случае при движении от сечення 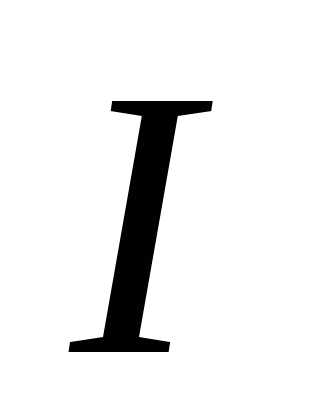 к сечению
к сечению 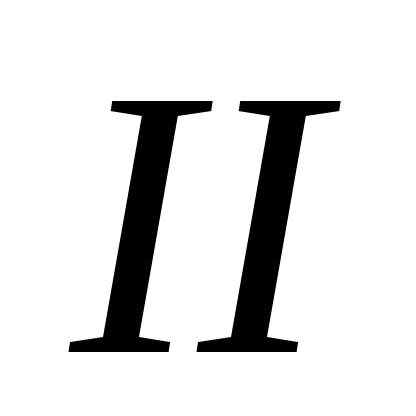
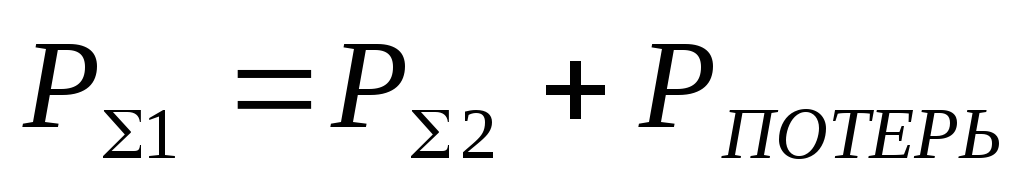 (12)
(12)
и окончательно закон Бернулли формулируется следующим образом: «При установившемся течении несжимаемой жидкости (газа) для различных сечений канала сумма давлений всех видов является постоянной».
Рассмотрим, что представляет собой потерянное давление, входящее в уравнение Бернулли.
При движении реального газа часть его энергии расходуется на преодоление трения и различных сопротивлений.
Потери на местные сопротивления возникают при резком изменении величины и направления скорости, при резком изменении сечения канала, при повороте канала или усложнении его сечения, при соударении потоков. Величину потерь энергии выражают в долях скоростного давления.
Потери
на трение  ,(Па)
можно определить по формуле
,(Па)
можно определить по формуле
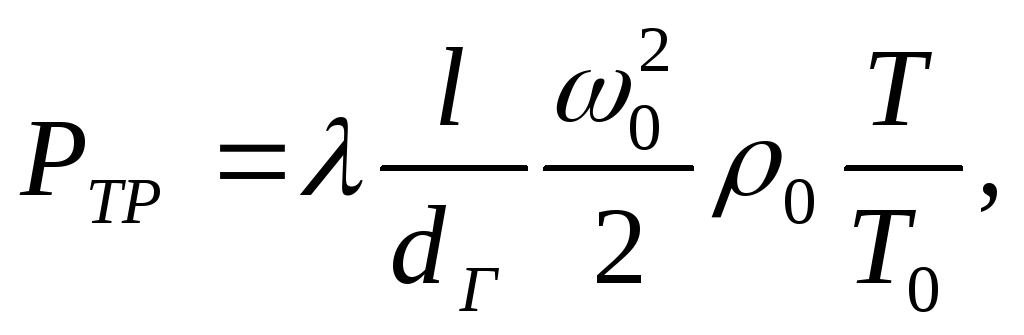 (13)
(13)
где  - коэффициент трения;
- коэффициент трения; 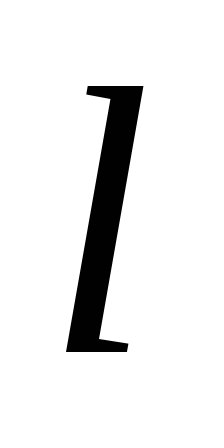 - длина канала, м;
- длина канала, м; 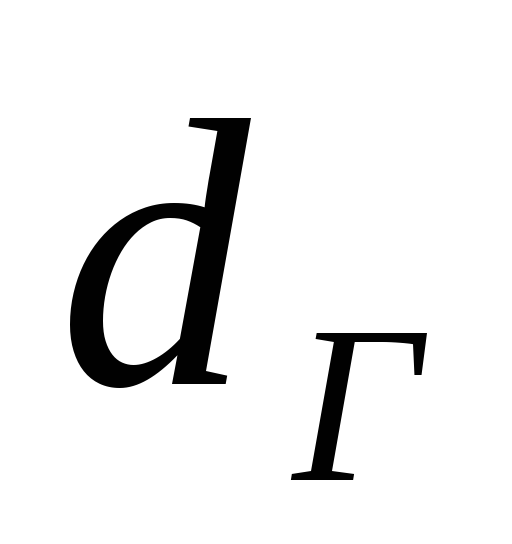 - гидравлический
диаметр канала, м;
- гидравлический
диаметр канала, м;
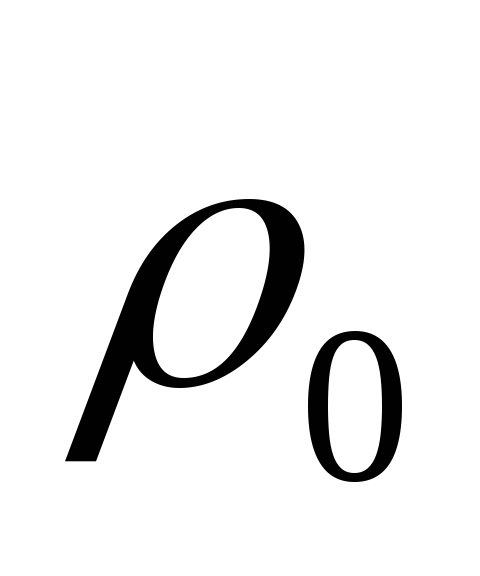 и
и 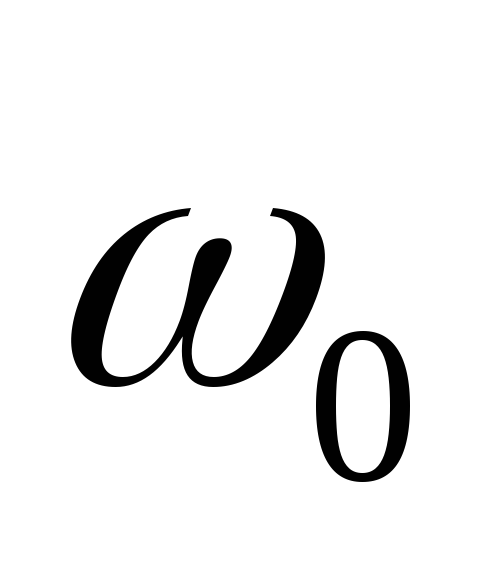 - плотность и скорость
жидкости
(газа) при нормальных условиях, т.е. при
атмосферном давлении
и температуре Т
о
,
равной 273 К; Т
- действительная
температура жидкости или газа, К.
- плотность и скорость
жидкости
(газа) при нормальных условиях, т.е. при
атмосферном давлении
и температуре Т
о
,
равной 273 К; Т
- действительная
температура жидкости или газа, К.
При ламинарном движении (Rе<2300) коэффициент трения зависит от критерия Rе
 .
(14)
.
(14)
При
турбулентном движении коэффициент
трения зависит не
только от критерия Re,
но и от относительной шероховатости
стенки канала (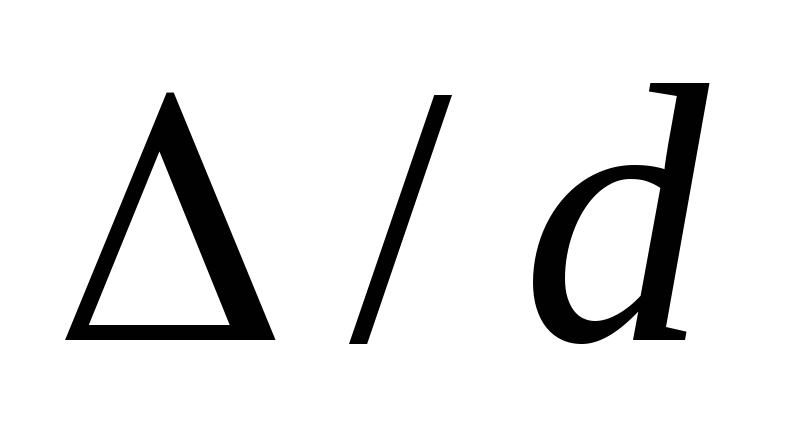 ),
равной
отношению абсолютной
шероховатости
),
равной
отношению абсолютной
шероховатости  (в мм) к диаметру канала
(в мм) к диаметру канала  :
:
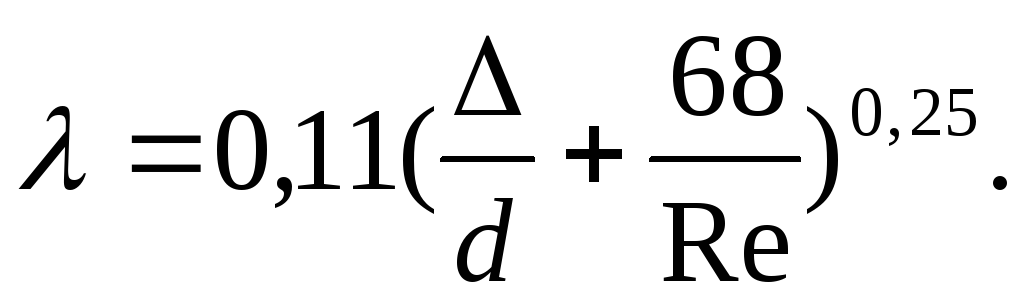
При
приближенных практических расчетах
коэффициент трения
 можно принимать
постоянным и равным для кирпичных
каналов 0,05, для металлических 0,04.
можно принимать
постоянным и равным для кирпичных
каналов 0,05, для металлических 0,04.
Потери на преодоление местных сопротивлений (Па), определяются по формуле
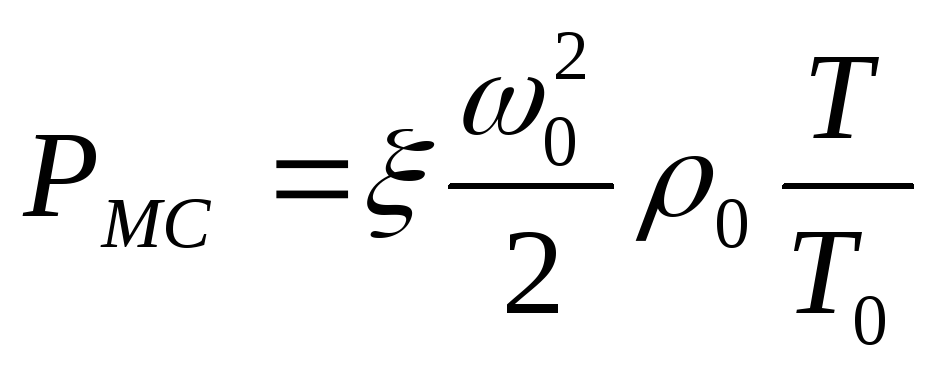 ,
,
где  - коэффициент местного сопротивления.
Его величина
зависит от формы местного сопротивления,
как правило,
определена опытным путем и приведена
в справочной литературе.
- коэффициент местного сопротивления.
Его величина
зависит от формы местного сопротивления,
как правило,
определена опытным путем и приведена
в справочной литературе.
Важнейшим расчетом, который выполняется для подавляющего большинства печей, является определение суммарных потерь давления на пути движения дымовых газов от печи до дымовой трубы. Суммарные потери используются при определении размеров дымовой трубы, которая рассчитывается из условия, что разрежение, создаваемое дымовой трубой, должно быть по абсолютной величине больше суммы всех сопротивлений, возникающих в дымовом тракте печи.
Таким образом, уравнение (закон) Бернулли находит очень широкое применение. Наряду с уравнением Бернулли важную роль в гидро- и аэродинамике играют также уравнение сплошности (или неразрывности течения) и уравнение импульсов Эйлера.
Уравнение сплошности.
В практических условиях наиболее распространенными являются такие процессы, при которых масса газа, протекающая по какому-то объему, остается неизменной. При этом, естественно, масса газа, втекающая в объем в единицу времени, должна быть равна массе вытекающего газа.
Следовательно,
можно написать, что 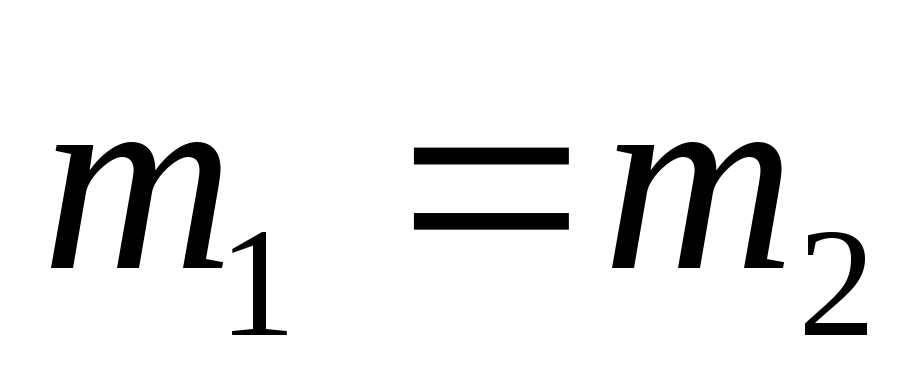 ,
или, учитывая,
что масса есть произведение скорости,
сечения потока
и плотности, получаем
,
или, учитывая,
что масса есть произведение скорости,
сечения потока
и плотности, получаем
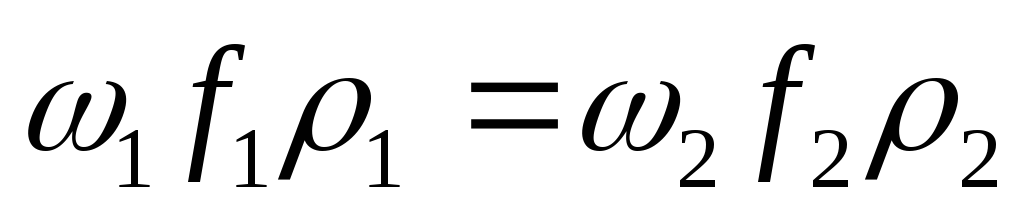 .
.
При
условии постоянства плотности (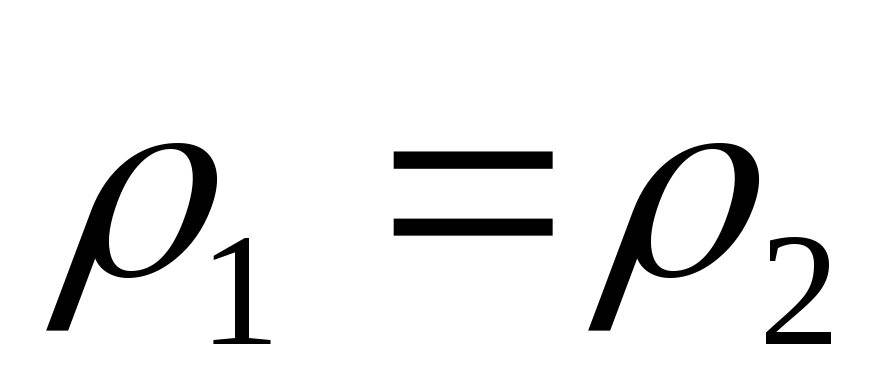 )
последнее
выражение принимает вид
)
последнее
выражение принимает вид
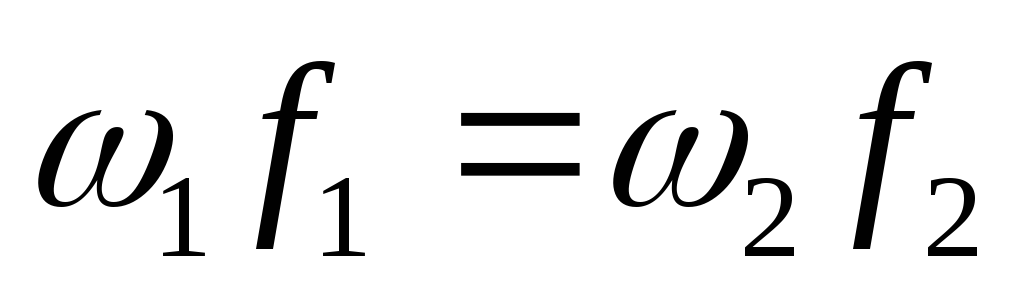 .
(15)
.
(15)
Если в качестве скорости принимать среднюю скорость потока, то выражение (15) применимо для практических расчетов при течении в трубах и каналах, причем средняя скорость потока определяется как частное от деления секундного объема среды, проходящего через данное сечение, на величину площади сечения, т. е.
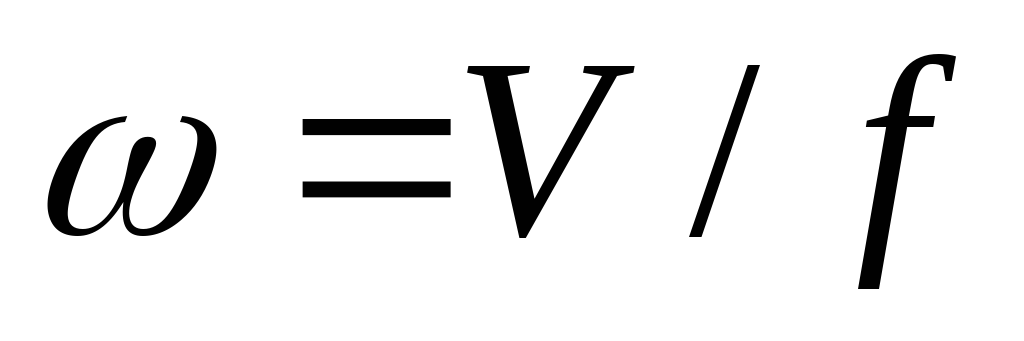 .
.
Уравнение импульсов Эйлера.
Уравнение импульсов (количества движения) Эйлера имеет важное значение для некоторых практических расчетов. Это уравнение применимо к какому-то воображаемому контуру, выделенному в общем потоке газа, через боковую поверхность которого ни движения, ни массообмена не происходит.
В подобном контуре под действием внешних сил (в потоке газа - под действием давления) происходит изменение количества движения газа. Если изменение импульсов проходящего газа и изменение внешних сил отнести к единице времени, то теорема импульсов Эйлера может быть сформулирована следующим образом: «Изменение импульса всех сил, приложенных к газу, проходящему через выделенный контур, равно результирующей внешних сил, действующих на данный контур».
Записывается это уравнение так:
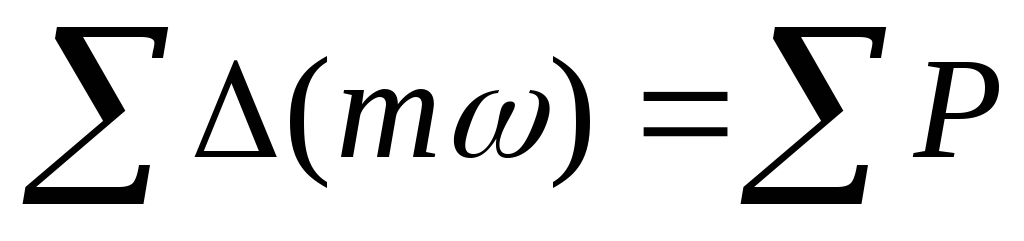 .
(16)
.
(16)
Применение уравнения импульсов будет проиллюстрировано ниже при рассмотрении струйных аппаратов.
Наиболее важные случаи применения уравнения Бернулли.
Истечение газов через отверстия и насадки
Истечение газов через отверстия и насадки наблюдается при работе горелок, форсунок, при выбивании газа через отверстия в стенах печи и в других случаях. Установим связь между количеством вытекающего газа и размерами отверстия и давлением, под которым происходит истечение. Для простоты возьмем истечение несжимаемого газа, температура которого в процессе истечения практически не изменяется.
Отверстия с острыми краями.
Предположим,
что из сосуда очень
больших размеров, давление в котором
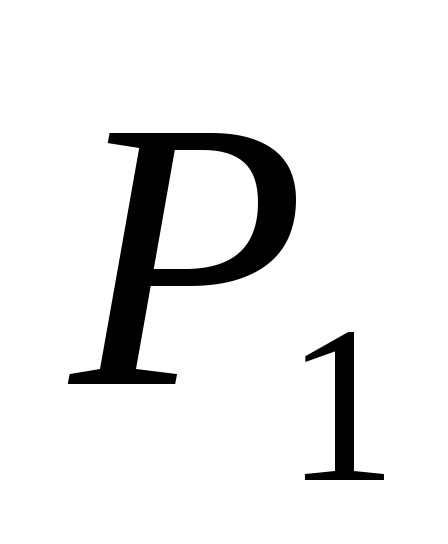 ,
газ
вытекает через
отверстие сечением
,
газ
вытекает через
отверстие сечением 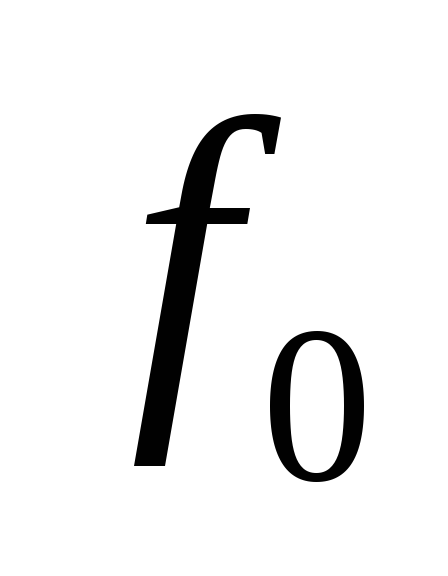 в среду с давлением
в среду с давлением 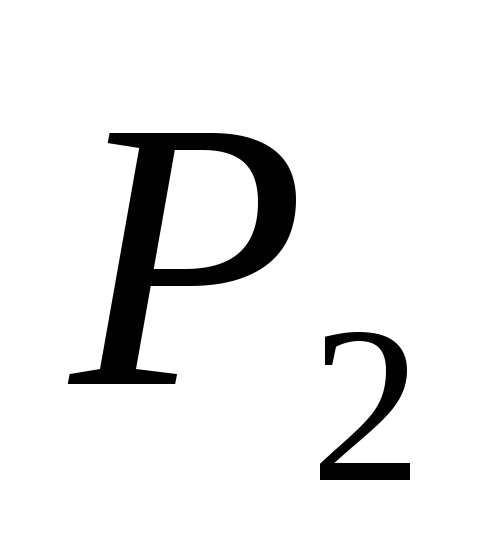 .
Для
определения скорости истечения газа
.
Для
определения скорости истечения газа 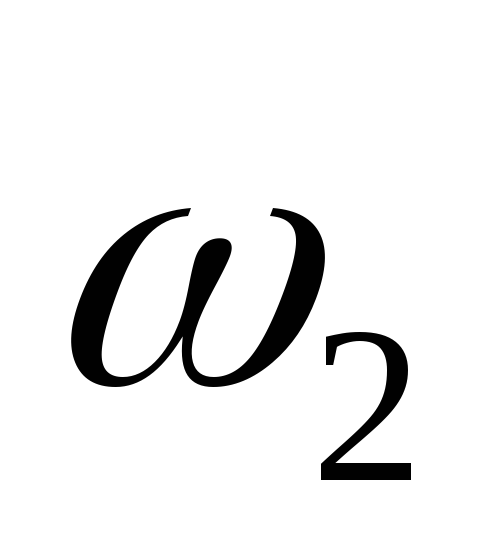 напишем уравнение
Бернулли для сечений
напишем уравнение
Бернулли для сечений 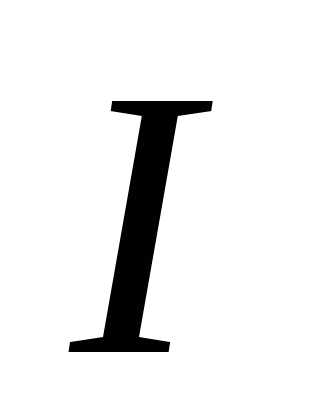 и
и
 (рис. 8). Поскольку
температура
газа неизменна, то
(рис. 8). Поскольку
температура
газа неизменна, то 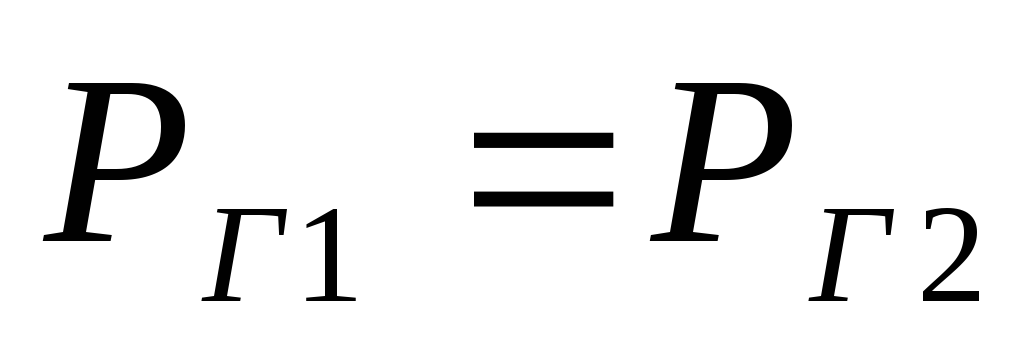 .
В
этом случае,
пренебрегая потерями, можно написать
.
В
этом случае,
пренебрегая потерями, можно написать
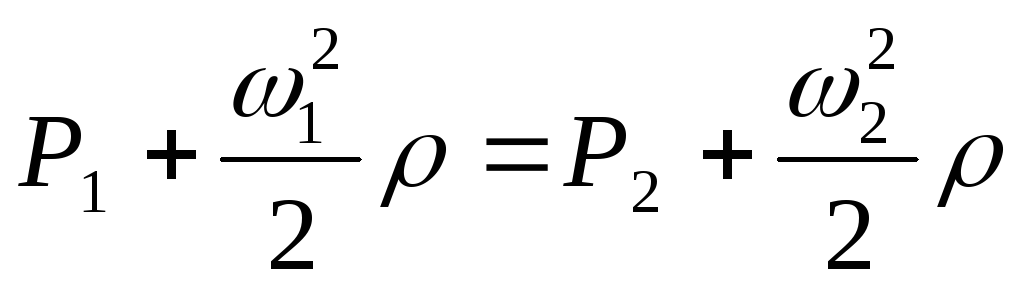 .
.
Вследствие большого
размера сосуда можно принять
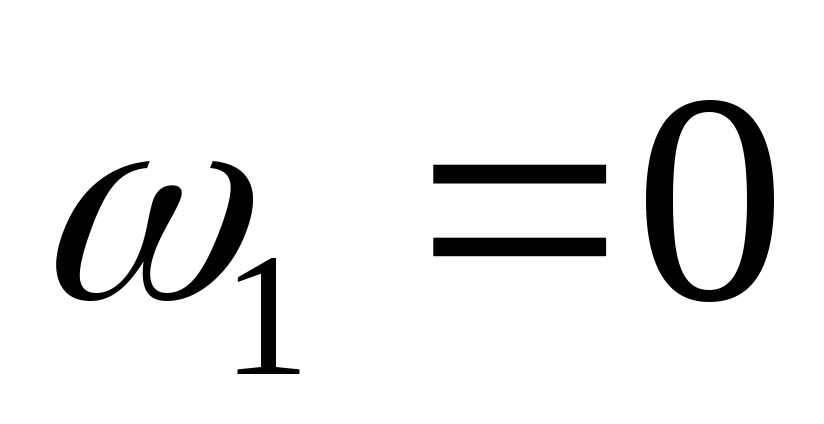 .
.
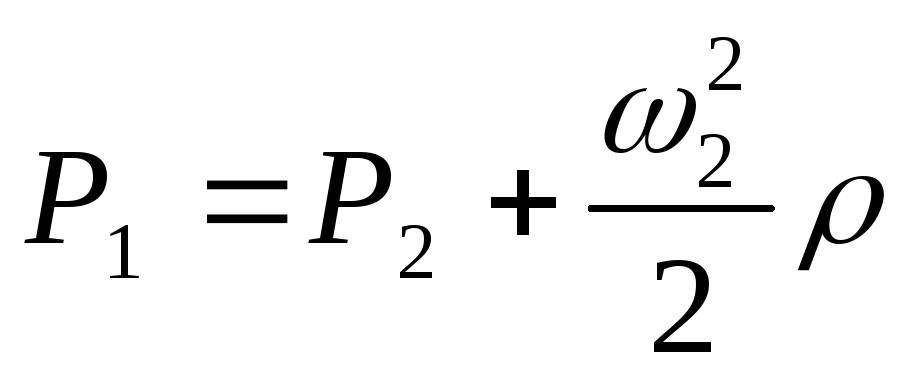 .
.
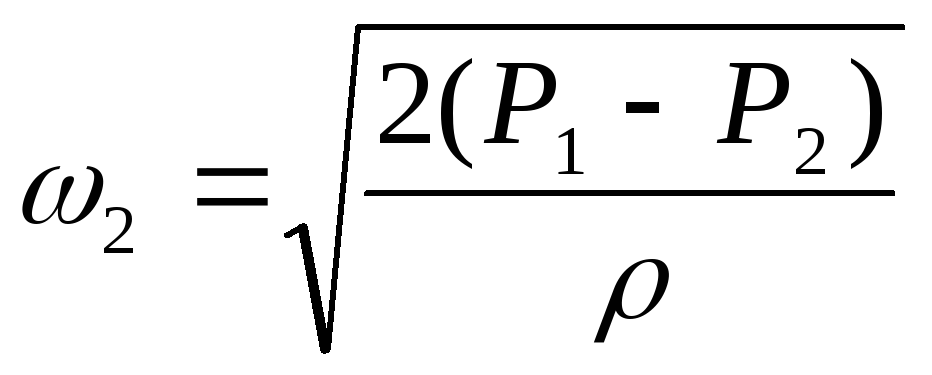 .м/с.
(17)
.м/с.
(17)
В силу инерции
частичек истекающего газа сечение струи
 меньше
сечения отверстия
меньше
сечения отверстия .
Отношение
.
Отношение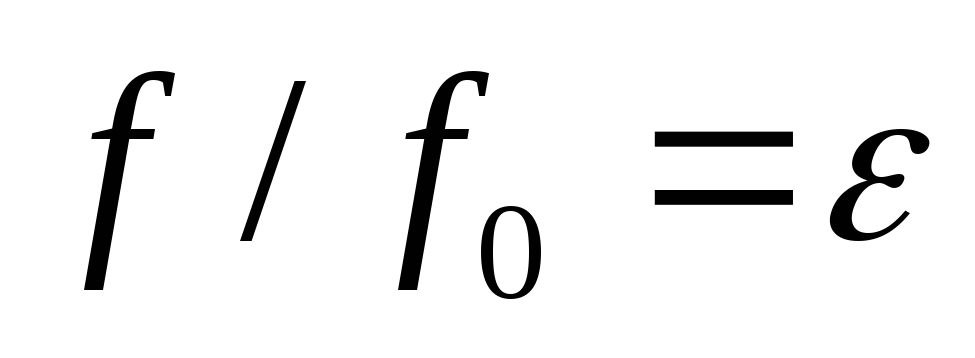 называется коэффициентом сжатия струи.
Скорость
называется коэффициентом сжатия струи.
Скорость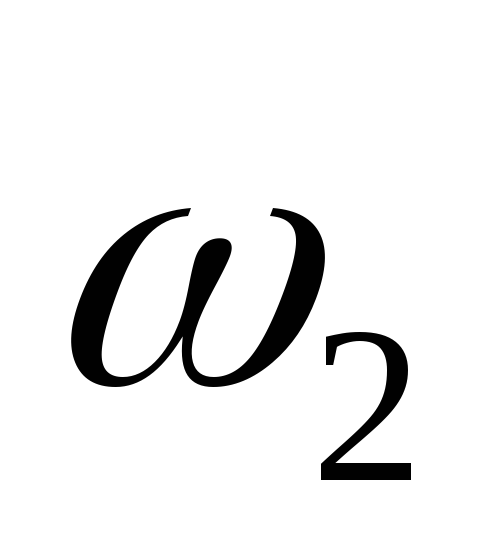 фактически
относится не ко всему сечению отверстия
фактически
относится не ко всему сечению отверстия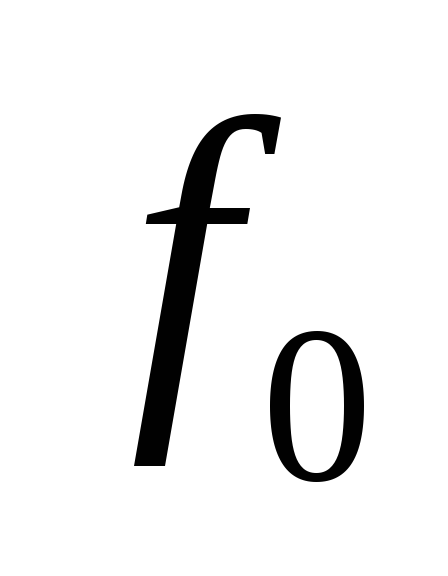 ,
а лишь к сечению струи
,
а лишь к сечению струи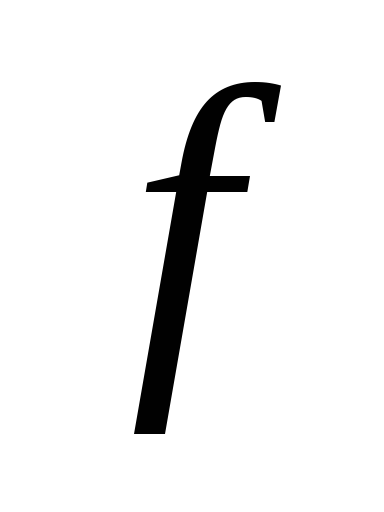 .
Для определения расхода газа через
отверстие
.
Для определения расхода газа через
отверстие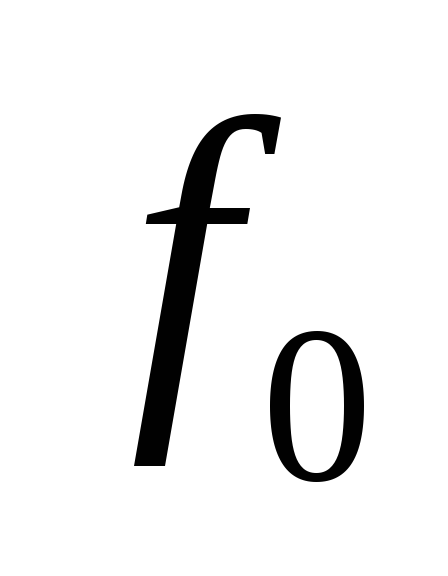 найдем
найдем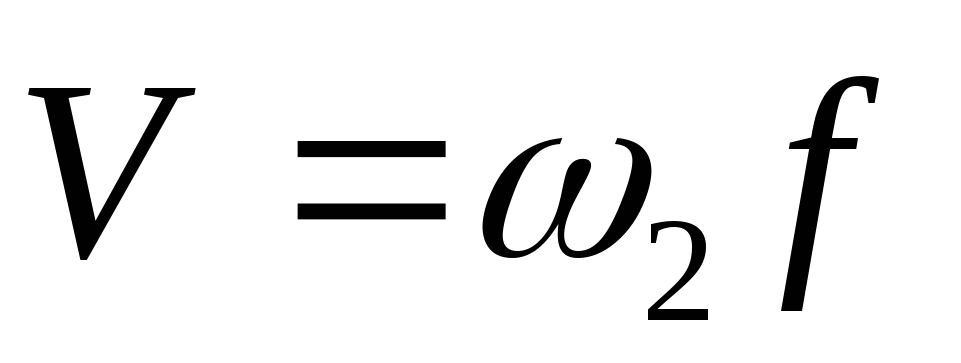 .
Но
.
Но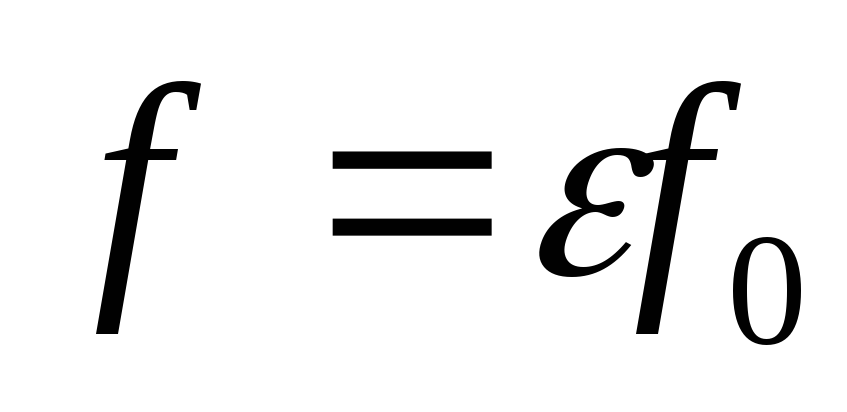 ,
следовательно,
,
следовательно,
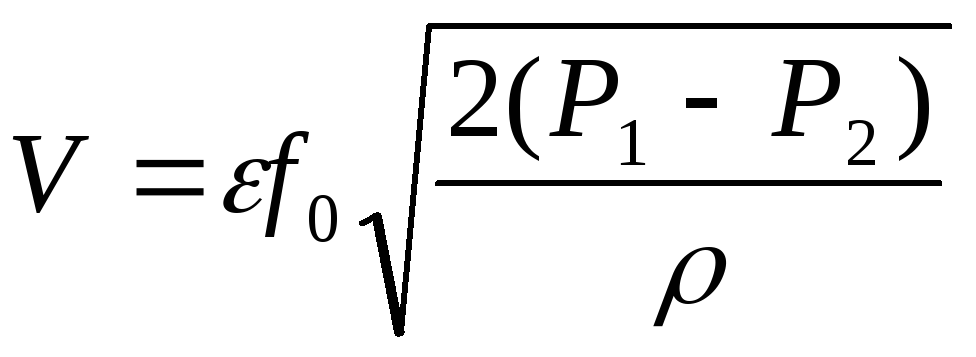 .
(18)
.
(18)
С учетом гидродинамических потерь при истечении через отверстие выражение (18) принимает вид (м 3 /с)


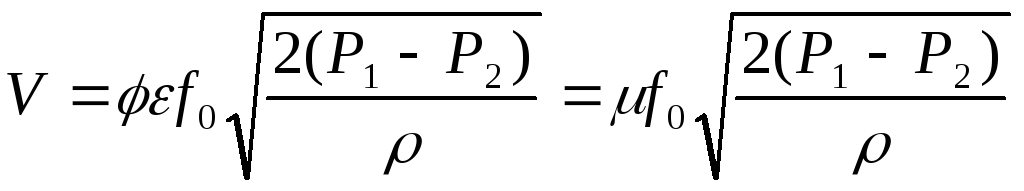 .
.
Смысл коэффициентов
 и
и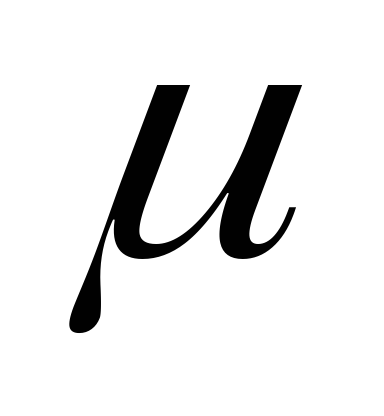 ясен из следующего примера.
ясен из следующего примера.
Истечение из
отверстия в стенке печи (рис. 9) – весьма
распространенный на практике случай.
Рассмотрим подобный случай истечения
(с учетом потерь) из отверстия сечением
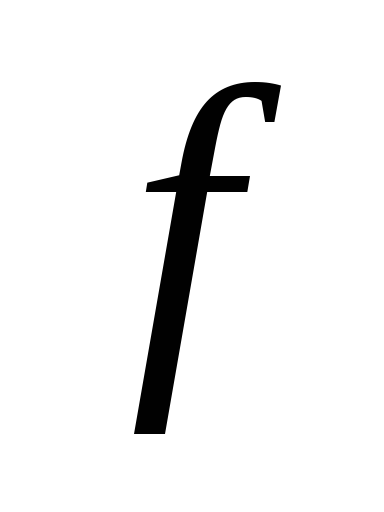 ,
расположенного на участкеH
от уровня пода печи. Напишем уравнение
Бернулли для сечения
,
расположенного на участкеH
от уровня пода печи. Напишем уравнение
Бернулли для сечения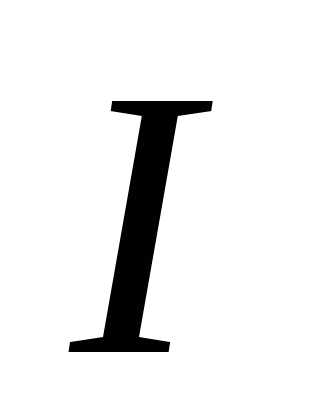 и
точкиA
в сечении
и
точкиA
в сечении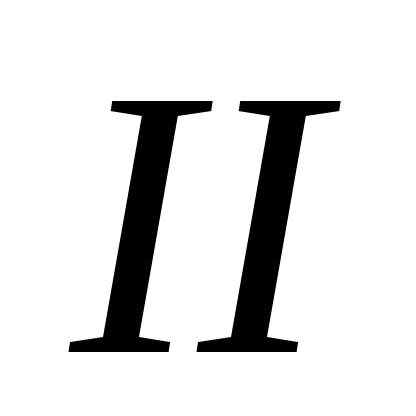 :
:
Скорость движения
газов в отверстии
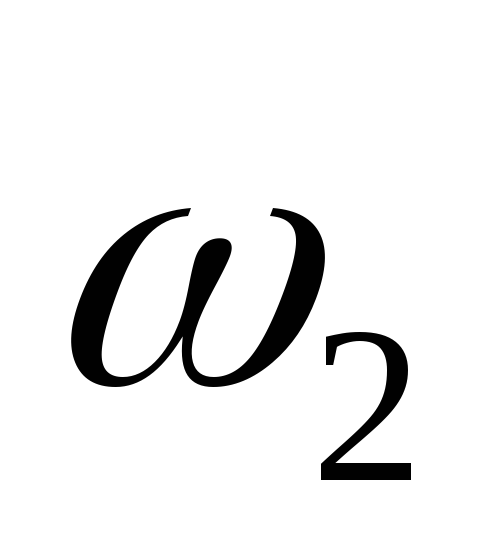 много больше скорости
много больше скорости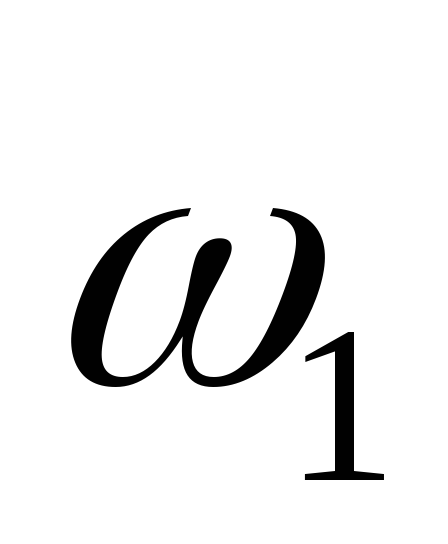 ;
исходя из
;
исходя из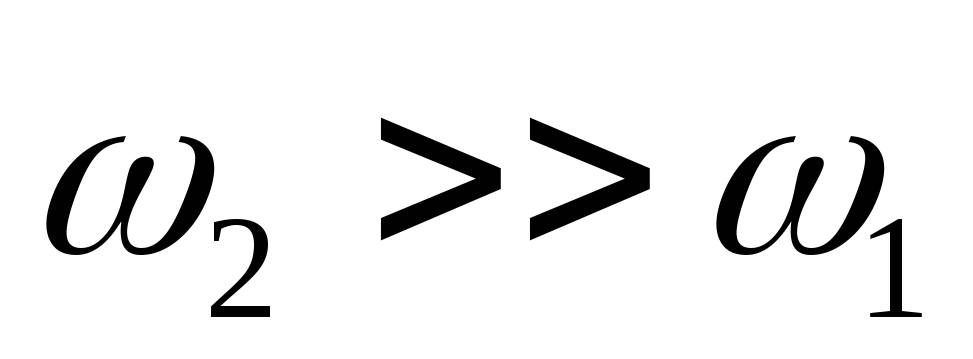 ,
принимаем
,
принимаем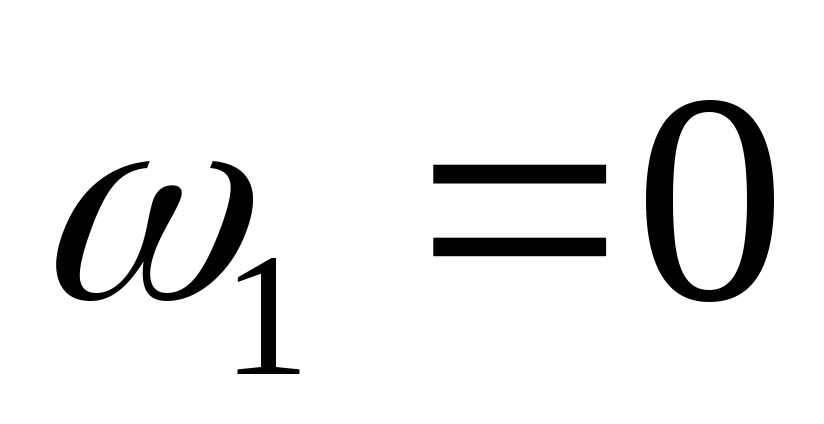 .
.
Как следует из
изложенного выше, потери на местные
сопротивления могут быть определены
как
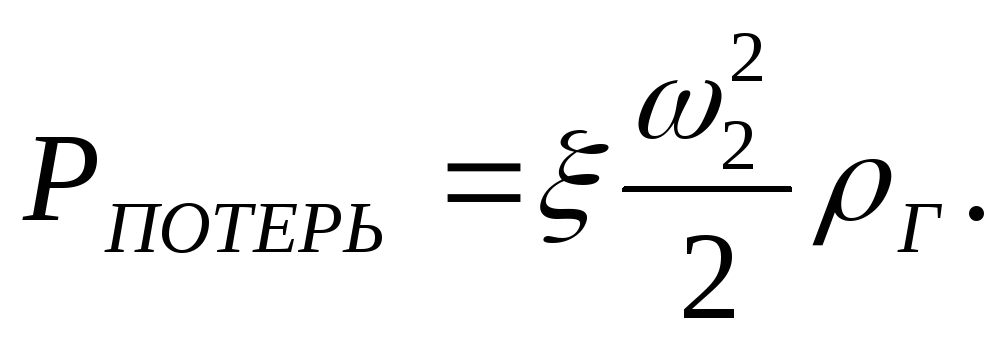
Так как печь
сообщается с атмосферой на уровне пода,
то пьезометрическое давление газа
внутри печи и давление воздуха снаружи
равны между собой и равны
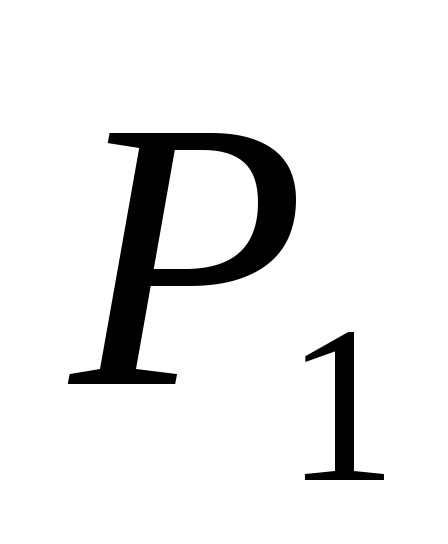 .
.
Давление
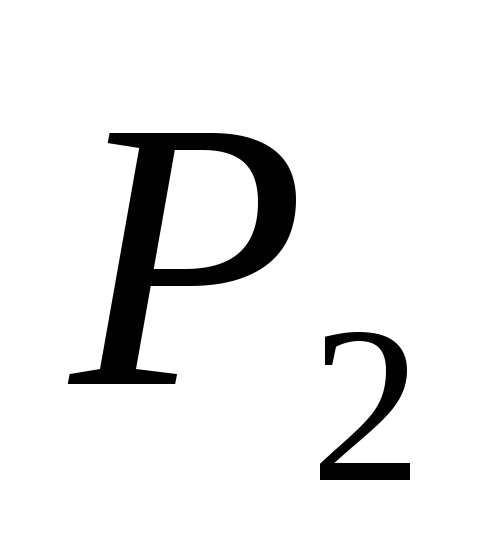 в точкеА
соответствует атмосферному
давлению на высотеН
от уровня
сечения
в точкеА
соответствует атмосферному
давлению на высотеН
от уровня
сечения
 ,
т.е.
,
т.е.
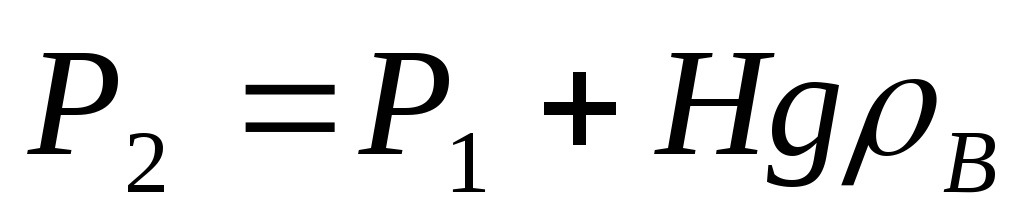 и
и
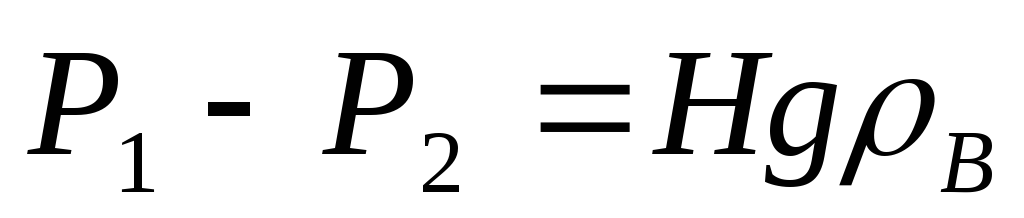 .
.
С использованием этих зависимостей уравнение Бернулли принимает вид
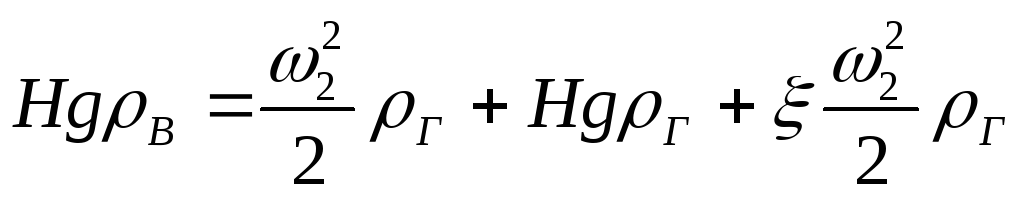
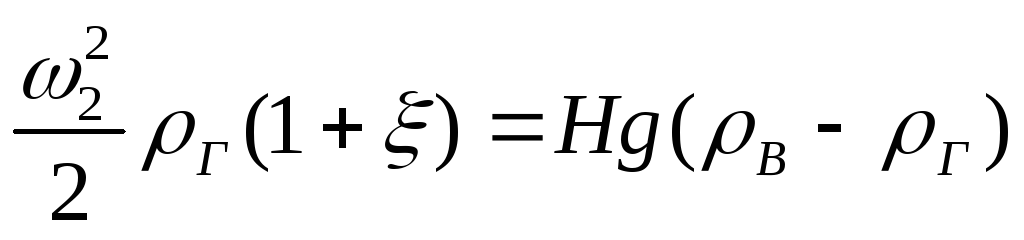 .
.
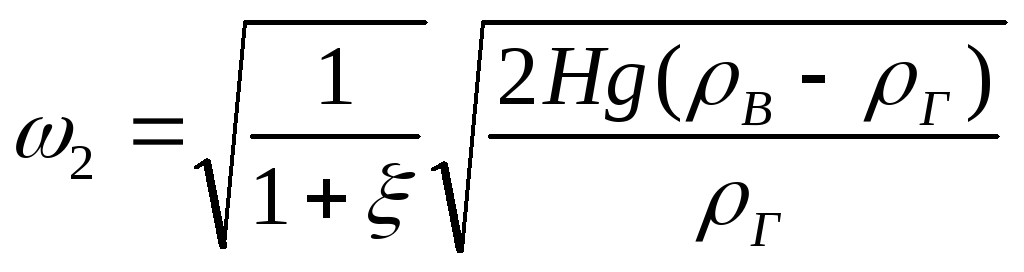 .
(19)
.
(19)
Величина
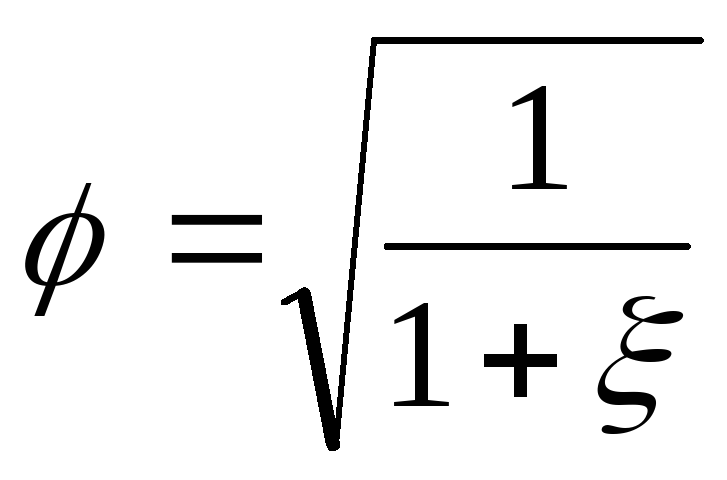 учитывает
гидравлическое сопротивление отверстия,
через которое происходит истечение.
Количество истекающей из рассматриваемого
течения среды (м 3 /с)
учитывает
гидравлическое сопротивление отверстия,
через которое происходит истечение.
Количество истекающей из рассматриваемого
течения среды (м 3 /с)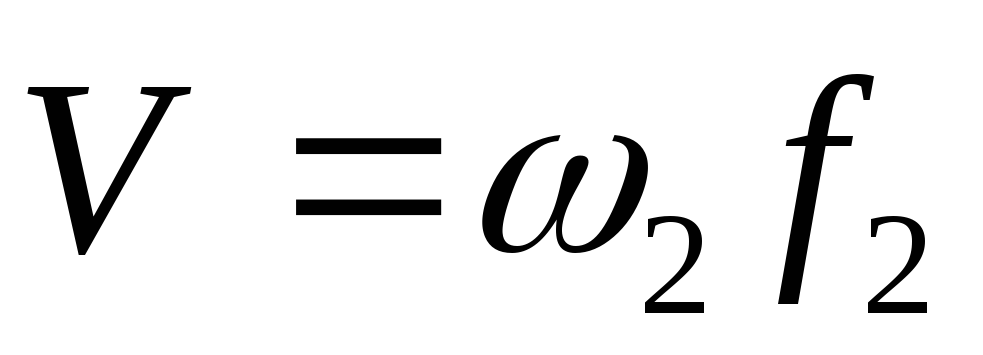 ,
где
,
где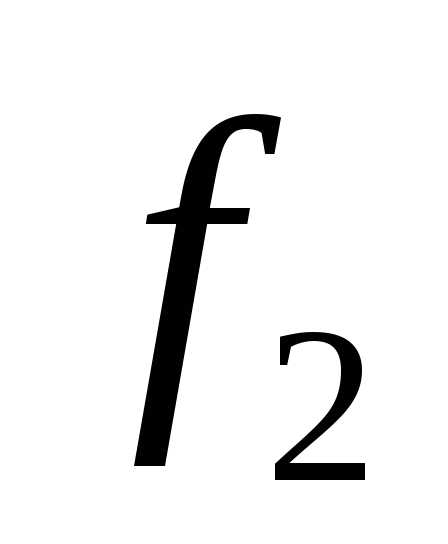 - сечение струи, м 2 .
- сечение струи, м 2 .
Но если использовать
понятие коэффициента сжатия струи
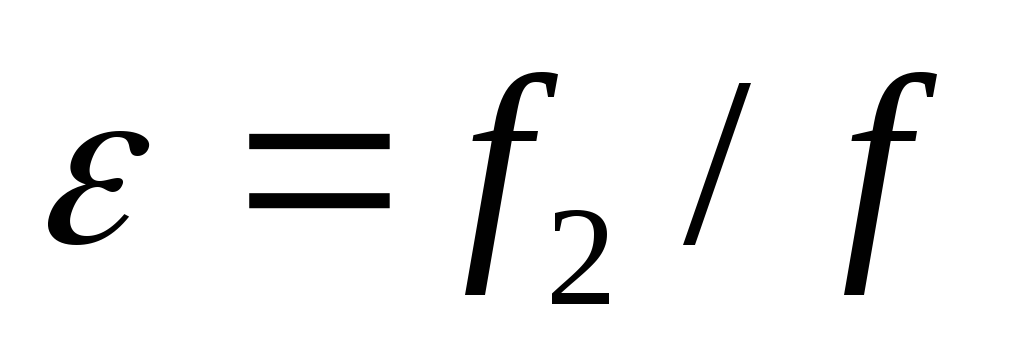 ,
то
,
то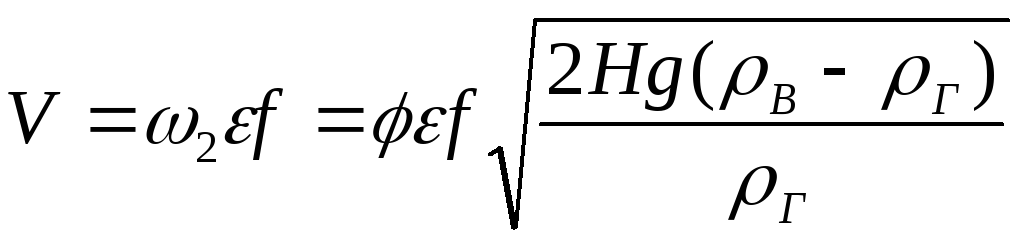 .
.
Произведение
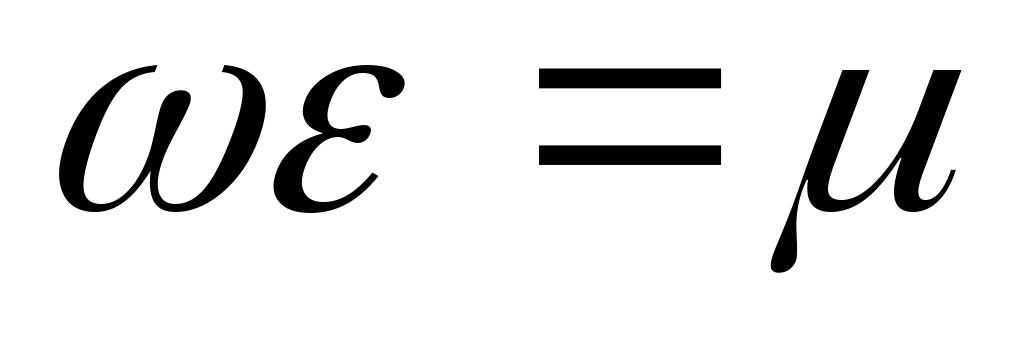 называют
коэффициентом расхода.
называют
коэффициентом расхода.
Истечение через насадки.
Насадкой называют короткий патрубок, присоединенный к отверстию в тонкой стенке. Длина насадки обычно составляет 3 – 4 его диаметров. Количество газа, протекающее через насадку, при прочих равных условиях зависит от формы входных кромок и формы самой насадки. Рассмотрим насадки трех видов, представленные на рис. 10. Пользуясь уравнением (19) получим для них

следующие расчетные формулы:
для насадки с острыми кромками:
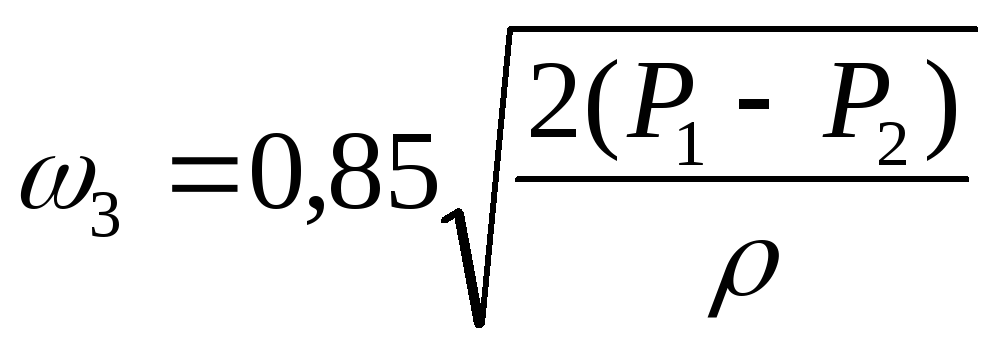 ;
;
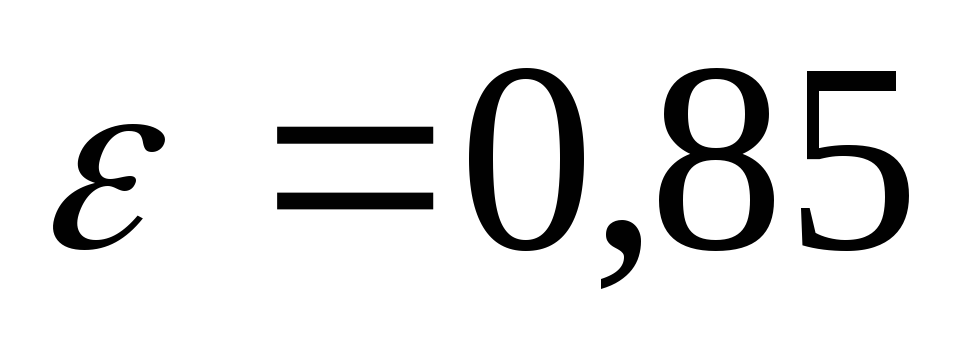 (20)
(20)
![]() .
(21)
.
(21)
Для насадок с закругленными кромками и диффузора:
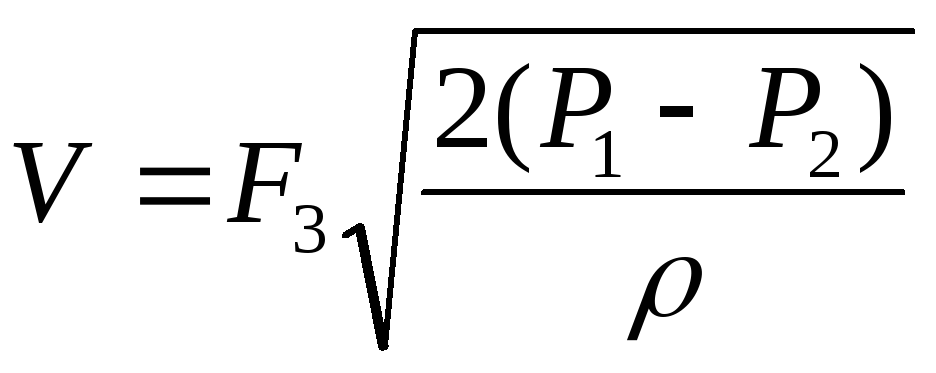 .
(22)
.
(22)
Для этих насадок
в сечении
 сечения
струи и отверстия равны друг другу и
поэтому здесь
сечения
струи и отверстия равны друг другу и
поэтому здесь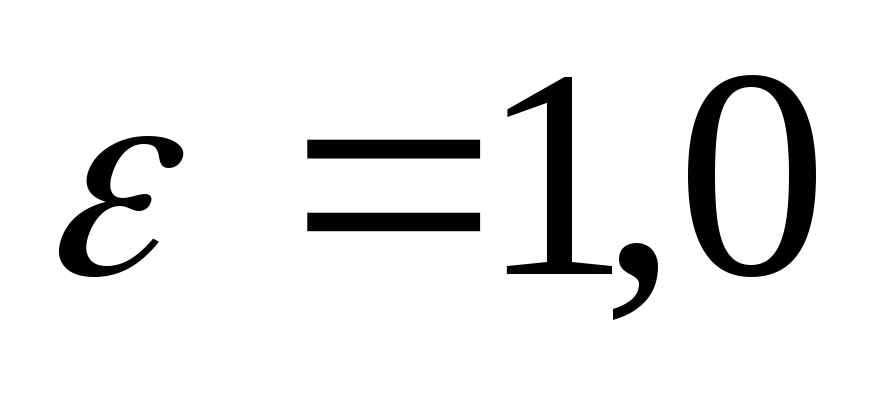 .
Сравнение выражений (20), (21) и (22) показывает,
что наибольший расход при одинаковом
значении
.
Сравнение выражений (20), (21) и (22) показывает,
что наибольший расход при одинаковом
значении![]() и при одинаковом минимальном сечении
насадок получается при истечения газа
через диффузор, так как площадь выходного
сечения у диффузора
и при одинаковом минимальном сечении
насадок получается при истечения газа
через диффузор, так как площадь выходного
сечения у диффузора больше, чем у насадок других типов. Угол
конусности диффузора не должен превышать
6 – 7º во избежание отрыва потока от
стенок диффузора.
больше, чем у насадок других типов. Угол
конусности диффузора не должен превышать
6 – 7º во избежание отрыва потока от
стенок диффузора.
Дымовая труба.
Дымовая труба служит для удаления продуктов сгорания из печи. Необходимое разрежение создается в дымовой трубе благодаря стремлению горячих газов подняться, обусловленному разностью плотностей холодного наружного воздуха и горячих газов.
Найдем зависимость
разряжения, создаваемого трубой, от
высоты трубы H
и
температуры газов. На рис. 11 представлена
схема дымовой трубы. За уровень отсчета
принимаем сечение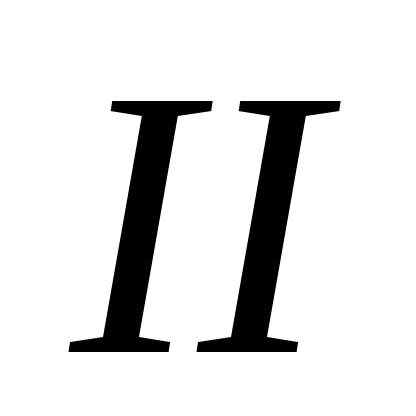 .
Напишем уравнение Бернулли в избыточных
давлениях для сечений
.
Напишем уравнение Бернулли в избыточных
давлениях для сечений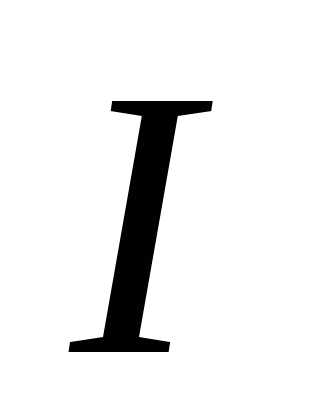 и
и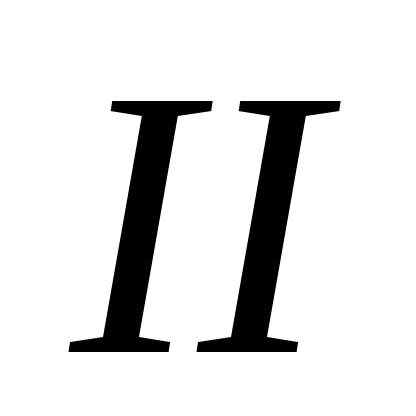 :
:
Труба в сечении
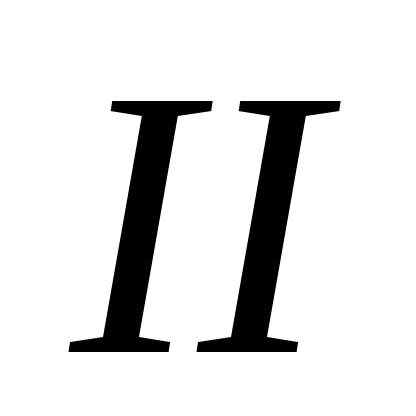 сообщается с атмосферой, поэтому
сообщается с атмосферой, поэтому .
Из приведенного выше уравнения следует,
что пьезометрическое давление в основании
трубы
.
Из приведенного выше уравнения следует,
что пьезометрическое давление в основании
трубы
Ввиду незначительных скоростей движения газов в трубе величины потерь, выражаемые в правой части приведенного выше уравнения тремя последними членами, значительно меньше абсолютной величины потери, выражаемой первым членом. Следовательно, пьезометрическое давление в основании трубы будет отрицательным, т.е. там будет разряжение. Умножив правую и левую части последовательно на минус единицу, получаем
Потери давления
в трубе
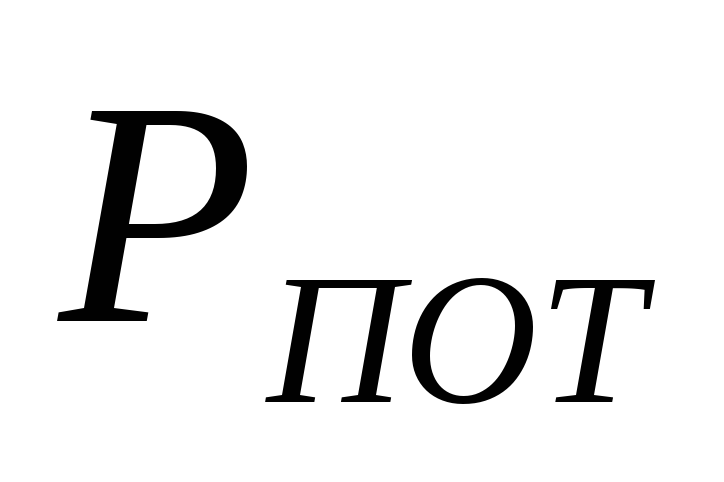 складываются из потерь на трение
складываются из потерь на трение и потерь, возникающих при выводе газов
из трубы в атмосферу и равных
и потерь, возникающих при выводе газов
из трубы в атмосферу и равных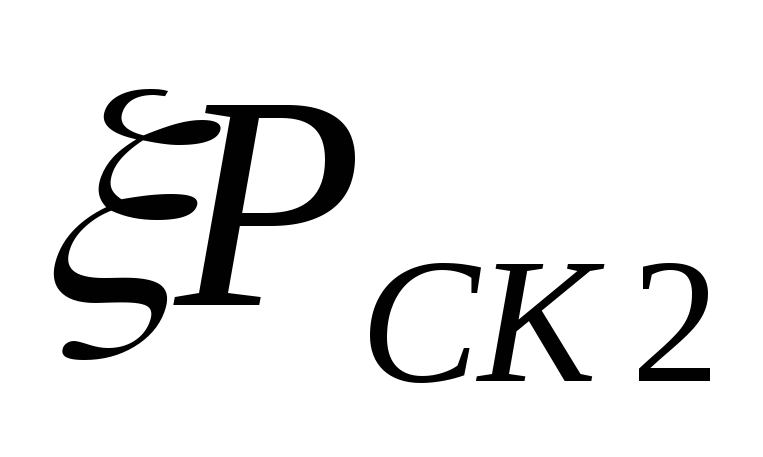 .
Учитывая, что коэффициент местного
сопротивления на выходе из трубы равен
единице (
.
Учитывая, что коэффициент местного
сопротивления на выходе из трубы равен
единице (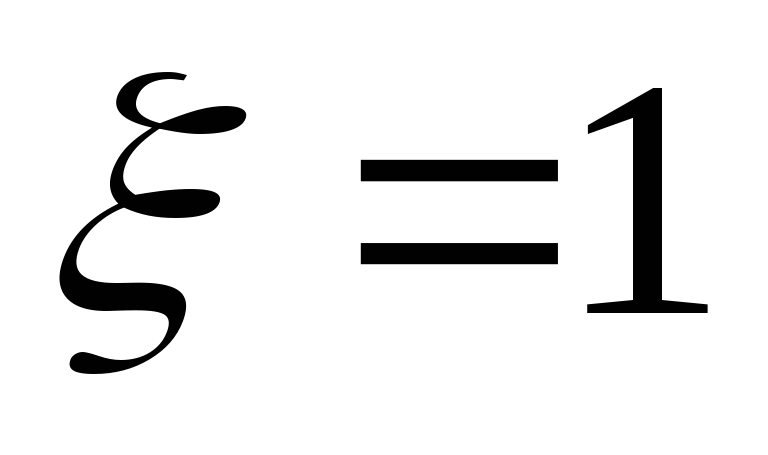 ),
можно написать, что
),
можно написать, что
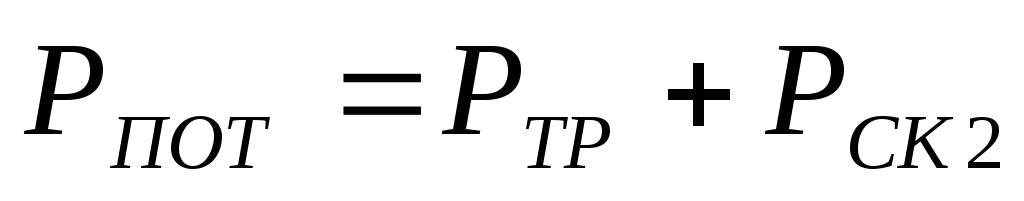 .
.
Вследствие этого уравнение (23):
Для того чтобы
получить окончательное выражение для
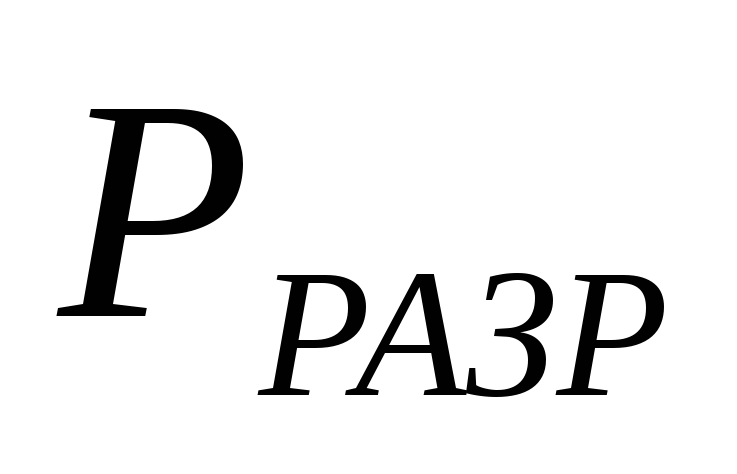 ,
в уравнение (24) необходимо подставить
все входящие в него величины. Температура
газов по высоте дымовой трубы и её
сечение существенно изменяются, поэтому
принимаемые в расчете плотность и
скорость движения газов в дымовой трубе
определяются по средней температуре
по высоте трубы. Величина геометрического
давления
,
в уравнение (24) необходимо подставить
все входящие в него величины. Температура
газов по высоте дымовой трубы и её
сечение существенно изменяются, поэтому
принимаемые в расчете плотность и
скорость движения газов в дымовой трубе
определяются по средней температуре
по высоте трубы. Величина геометрического
давления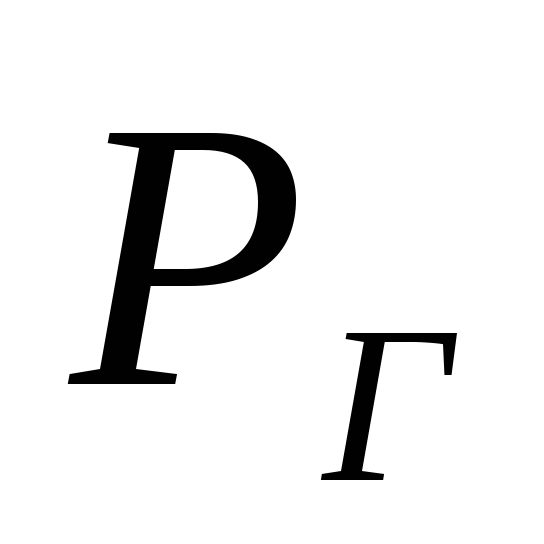 ,
входящего в уравнение (24), выражается
уравнением (3). Динамические давления
будут соответственно равны
,
входящего в уравнение (24), выражается
уравнением (3). Динамические давления
будут соответственно равны
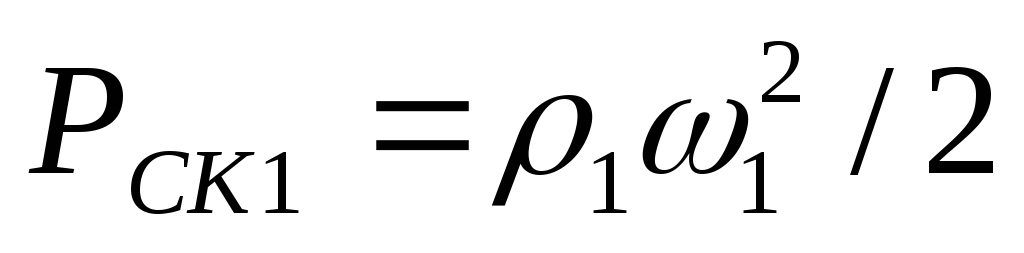 и
и
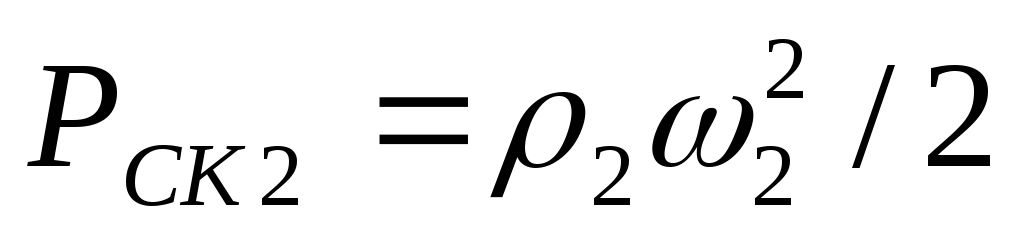 .
.
Потери давления на трение находят по уравнению
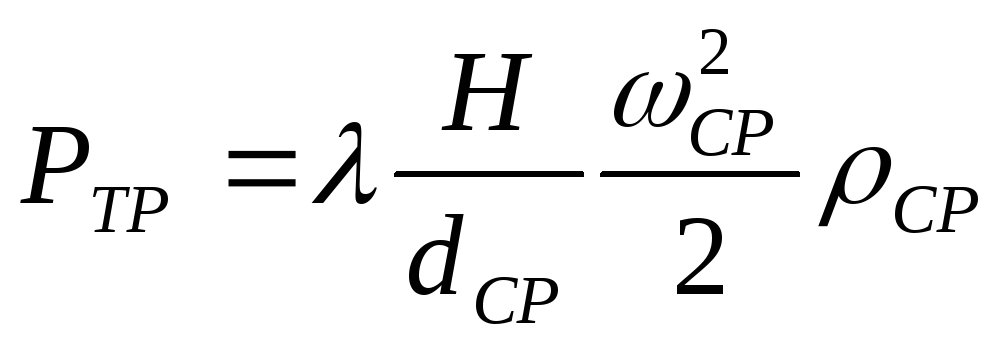 .
.
Подставив в
уравнение (24) значения
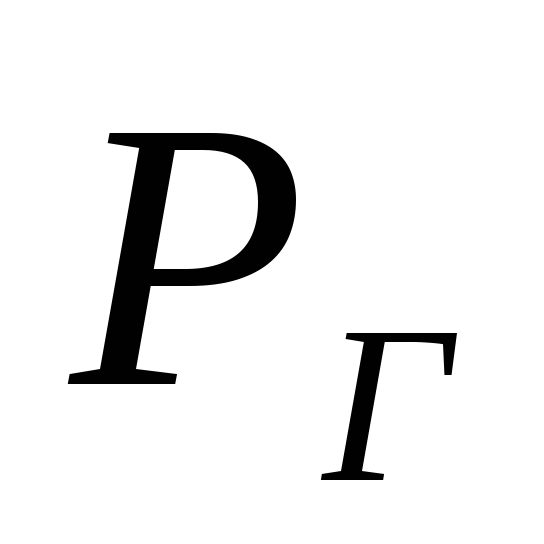 ,
,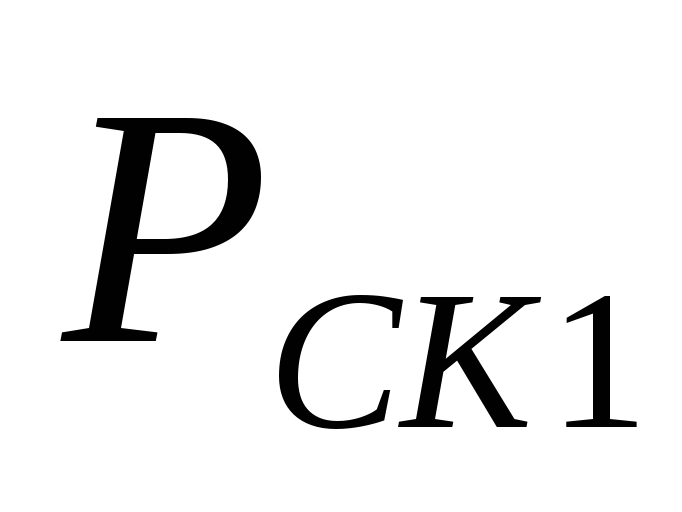 ,
,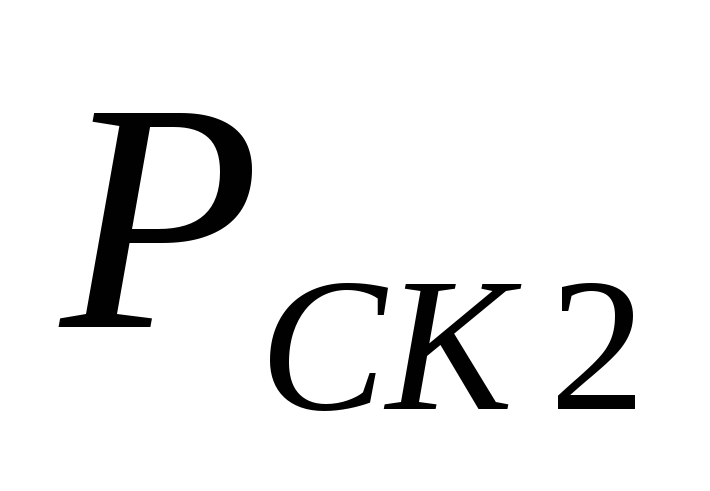 ,
, и выразив их через скорости и плотности
при нормальных условиях (
и выразив их через скорости и плотности
при нормальных условиях (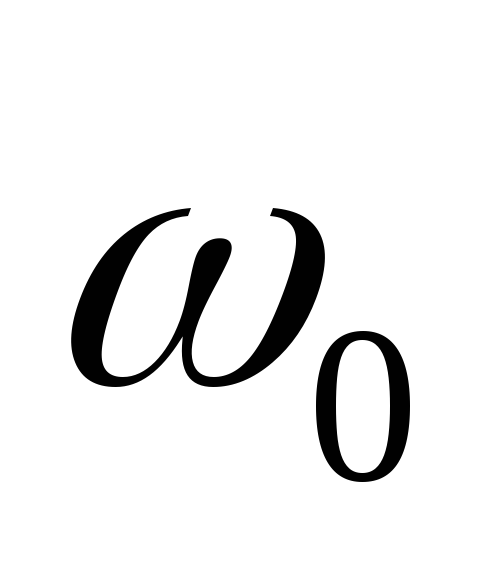 и
и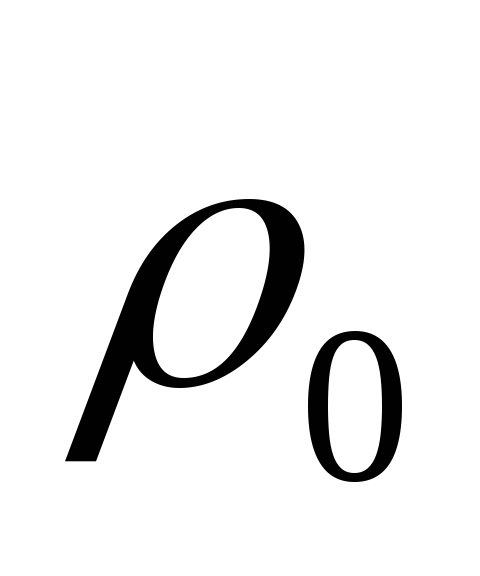 )
по указанным выше выражениям, окончательно
получаем (Па)
)
по указанным выше выражениям, окончательно
получаем (Па)
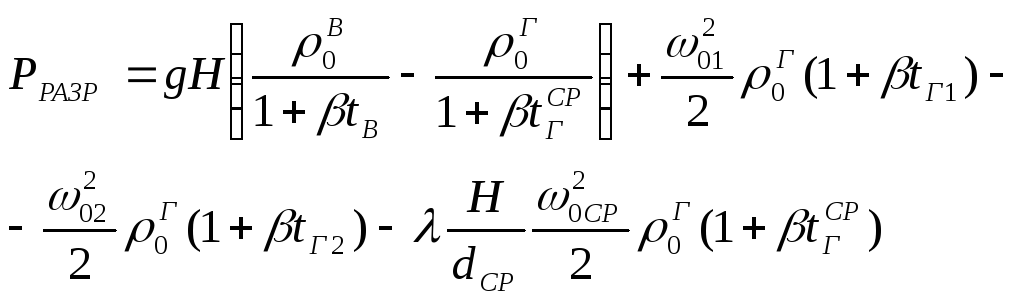 ,
(25)
,
(25)
где
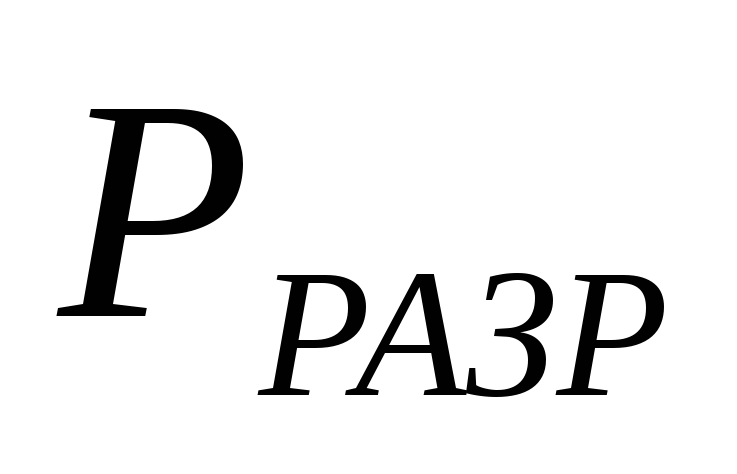 - действительное разрежение трубы в
основании дымовой трубы (сечение
- действительное разрежение трубы в
основании дымовой трубы (сечение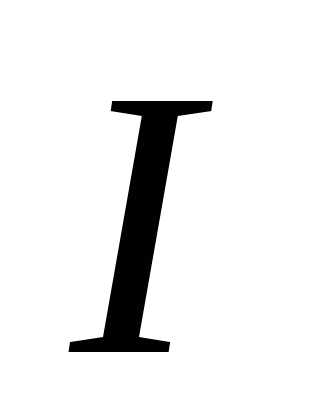 ),
Па;
),
Па;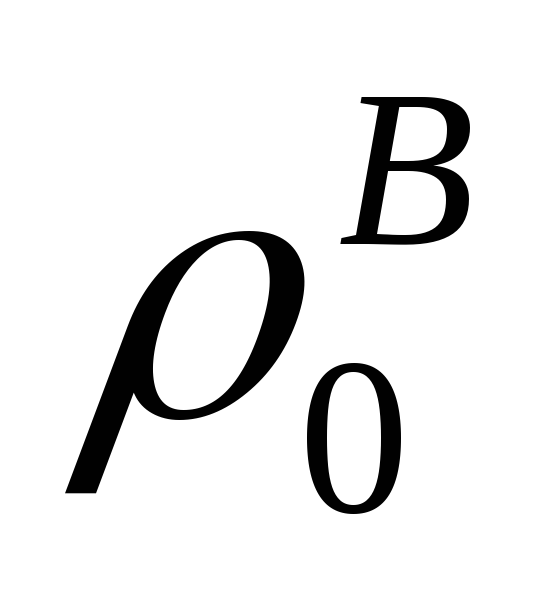 и
и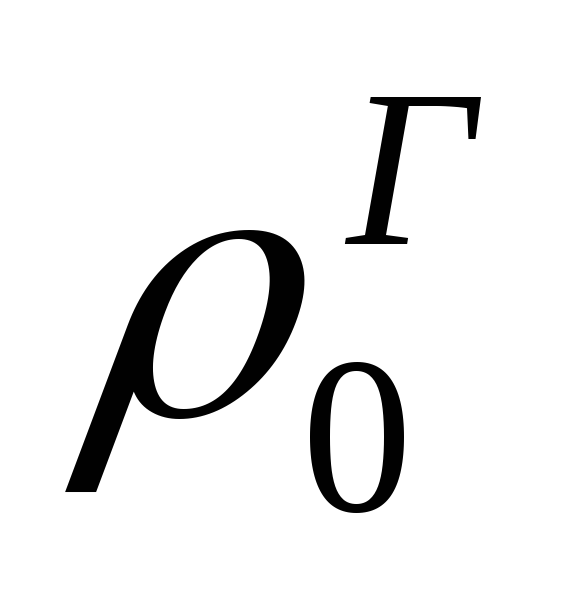 - плотность соответственно воздуха и
газов при нормальных условиях, кг/м 3 ;
- плотность соответственно воздуха и
газов при нормальных условиях, кг/м 3 ;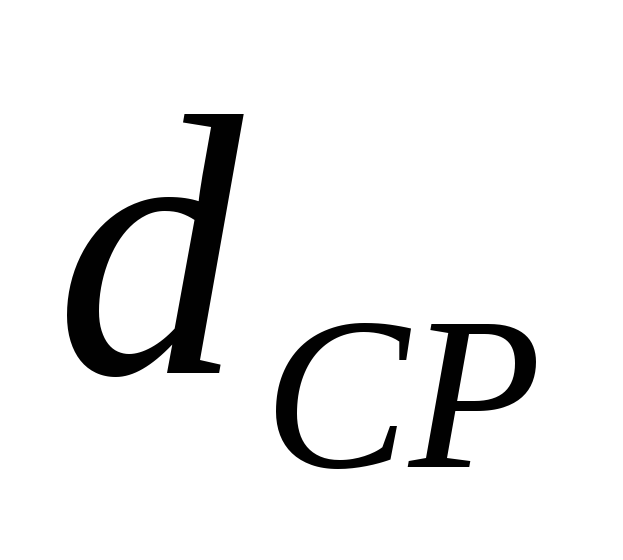 - средний по высоте диаметр трубы, м;
- средний по высоте диаметр трубы, м;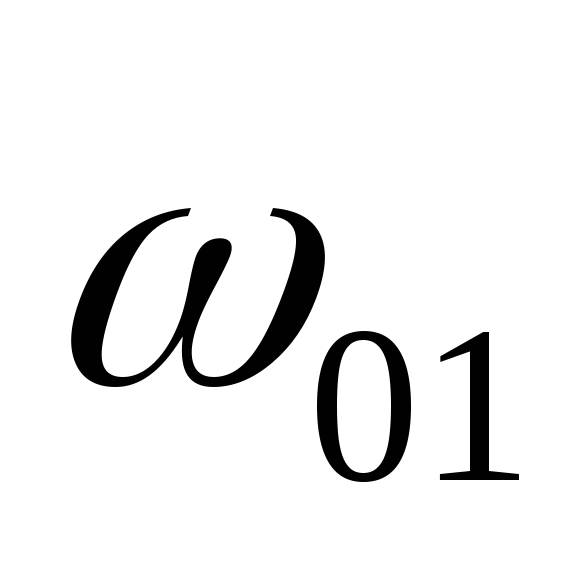 и
и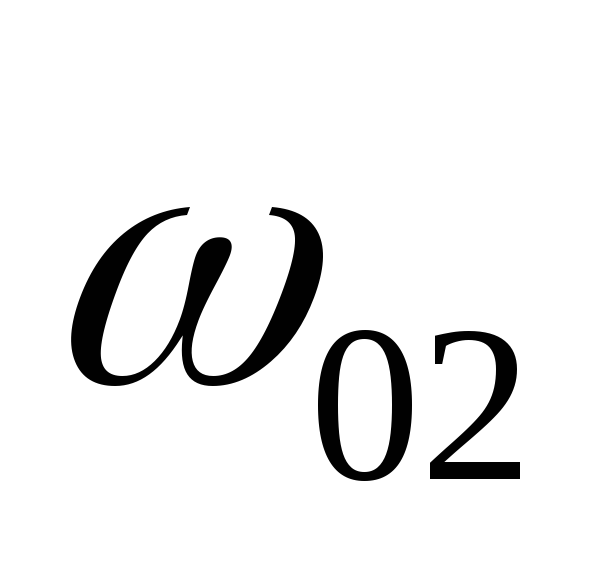 -
скорость газов в сечениях
-
скорость газов в сечениях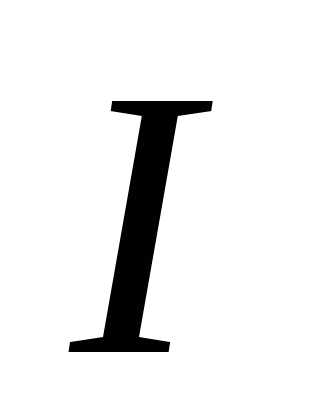 (в основании трубы) и
(в основании трубы) и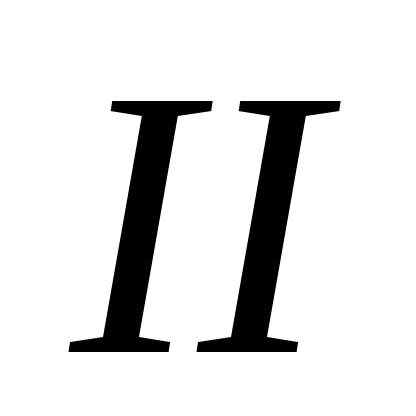 (в устье трубы) при 0ºС, м/с;
(в устье трубы) при 0ºС, м/с;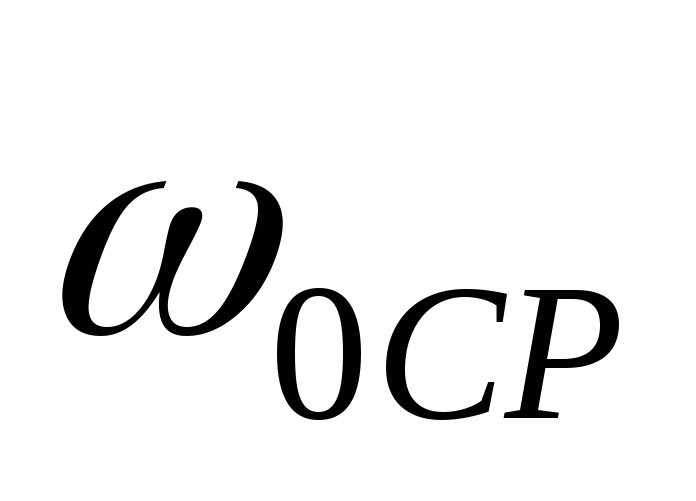 - средняя скорость газов по высоте трубы
при 0ºС, м/с;
- средняя скорость газов по высоте трубы
при 0ºС, м/с;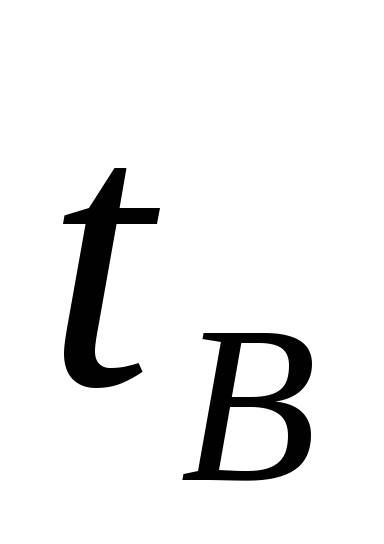 - температура окружающего воздуха, ºС;
- температура окружающего воздуха, ºС;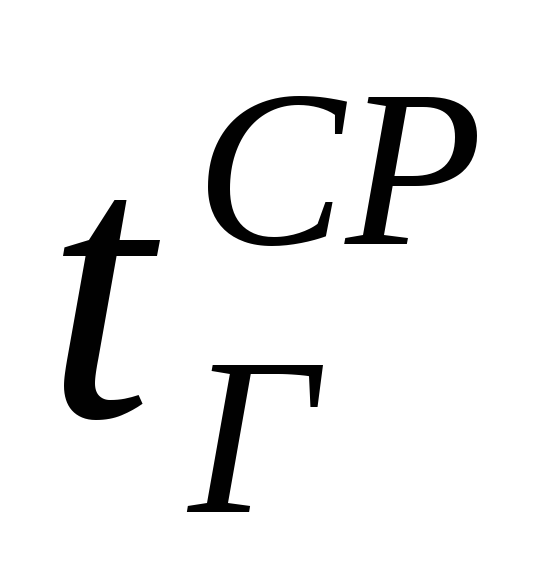 -
средняя температура газов по высоте
трубы, ºС;
-
средняя температура газов по высоте
трубы, ºС;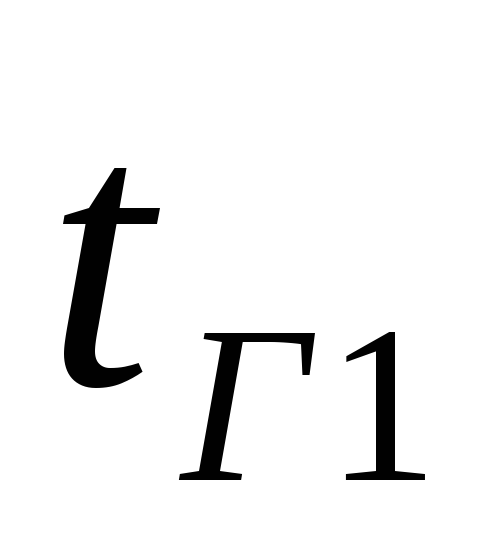 и
и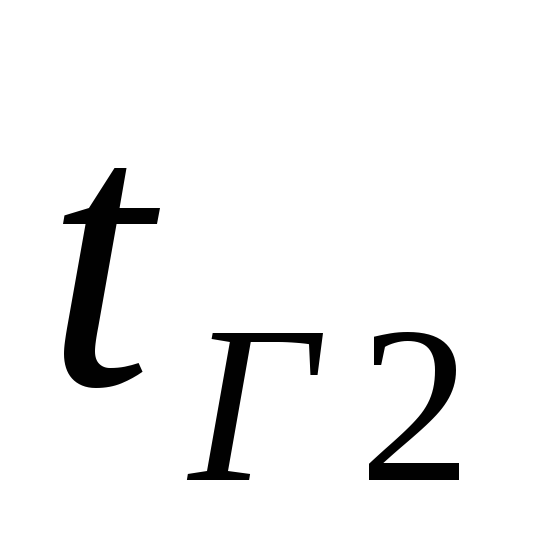 - температура газов в сечениях
- температура газов в сечениях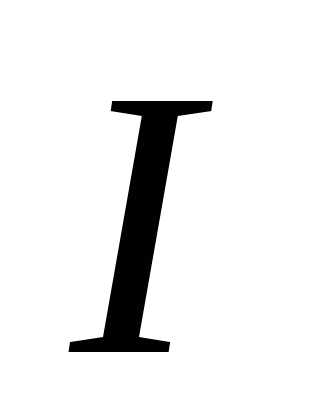 и
и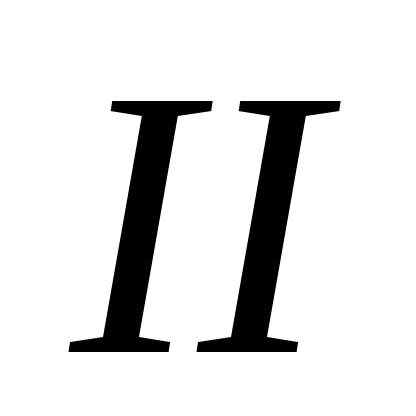 ,
ºС.
,
ºС.
Если учесть, что
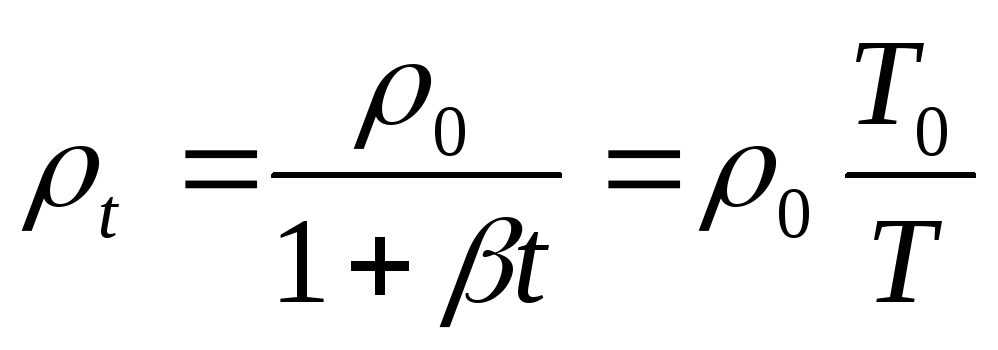 ,
,
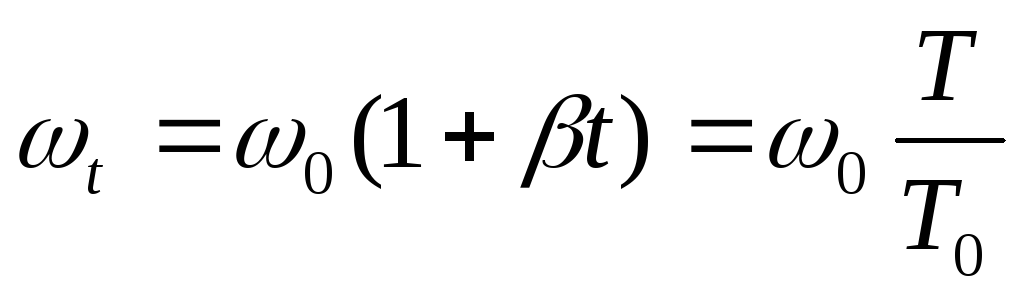 ,
где
,
где
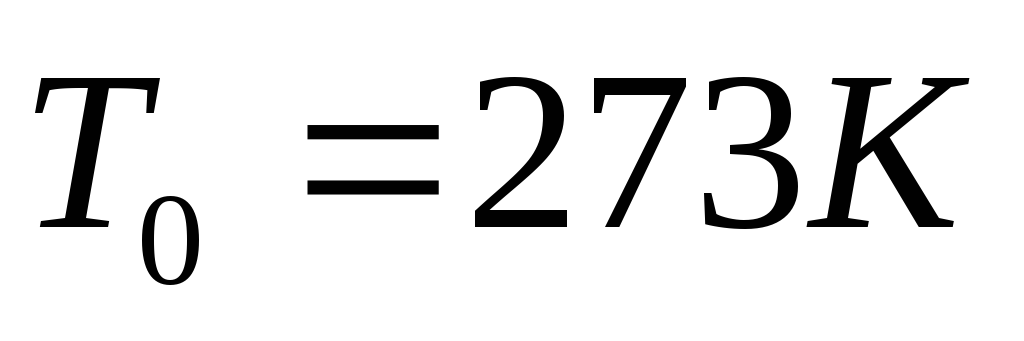 ,
то выражение (25) может быть переписано
следующим образом:
,
то выражение (25) может быть переписано
следующим образом:
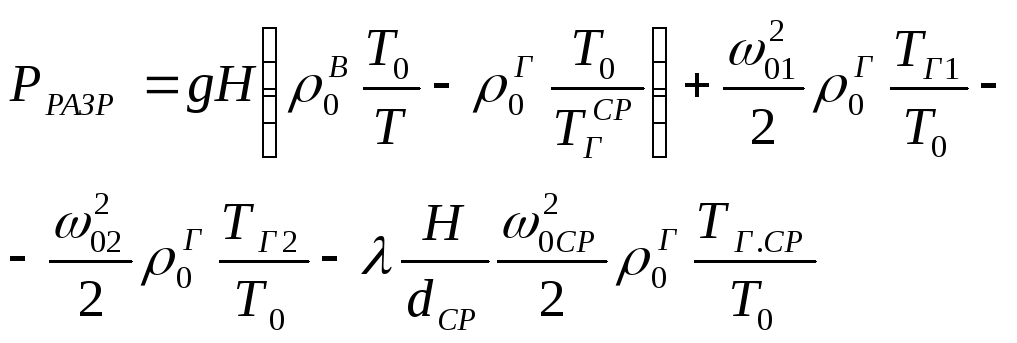 .
.
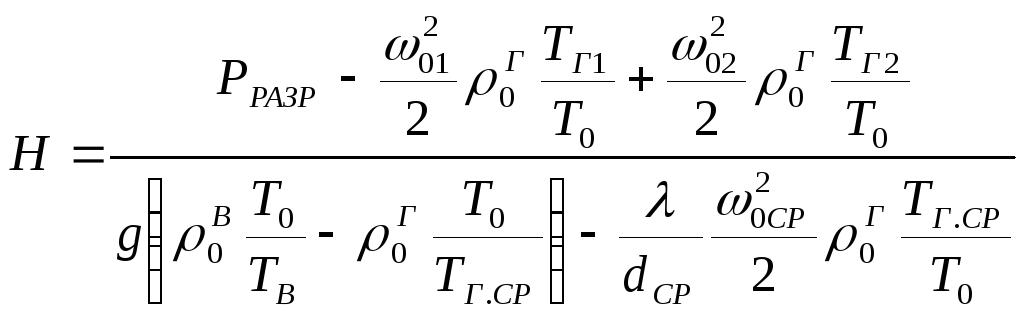 м.
(26)
м.
(26)
В расчетах разряжение
в основании дымовой трубы принимают
обычно с запасом, равным
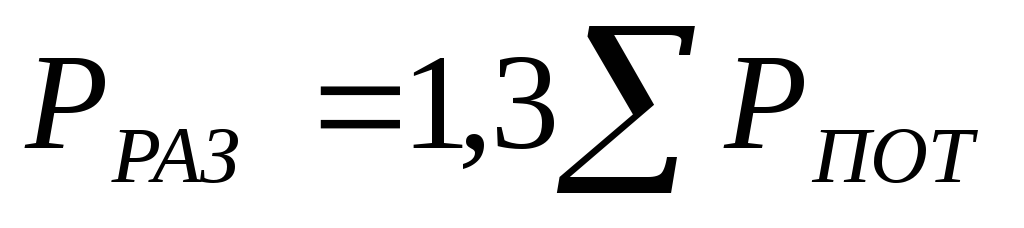 .
Величина
.
Величина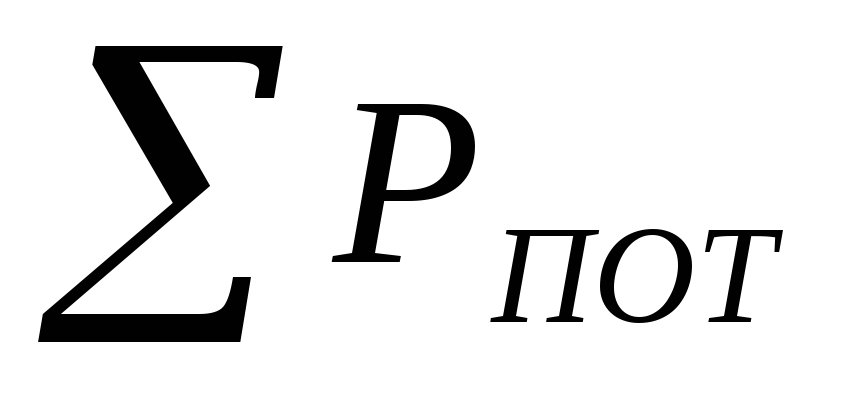 представляет собой суммарные потери
давления на пути движения газов от печи
до основания дымовой трубы..
представляет собой суммарные потери
давления на пути движения газов от печи
до основания дымовой трубы..
При расчете дымовой
трубы внутренний диаметр в устье ее
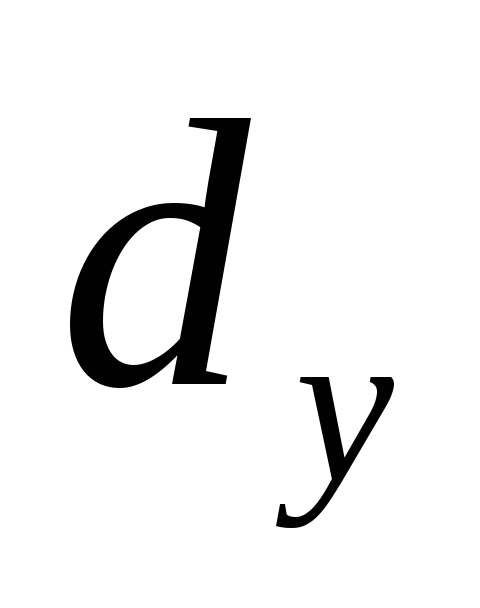 (на
выходе) принимают, исходя из скорости
газов, равной 3 – 10 м/с (при скорости
выхода газов, меньшей 3 м/с, при ветре
может происходить их задувание в трубу).
Кирпичные и железобетонные дымовые
трубы для большей устойчивости делают
более широкими в основании. При расчетах
внутренний диаметр в основании трубы
(на
выходе) принимают, исходя из скорости
газов, равной 3 – 10 м/с (при скорости
выхода газов, меньшей 3 м/с, при ветре
может происходить их задувание в трубу).
Кирпичные и железобетонные дымовые
трубы для большей устойчивости делают
более широкими в основании. При расчетах
внутренний диаметр в основании трубы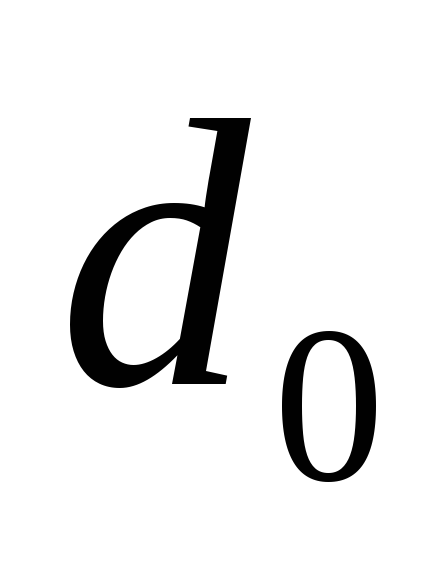 принимают в 1,5 раза больше внутреннего
диаметра устья трубы
принимают в 1,5 раза больше внутреннего
диаметра устья трубы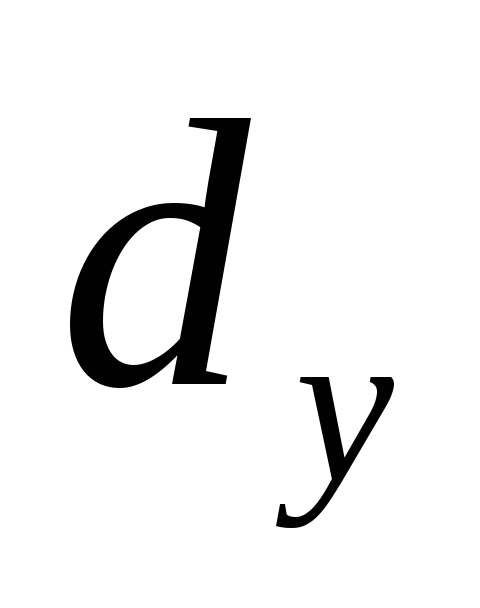 ,
т.е.
,
т.е.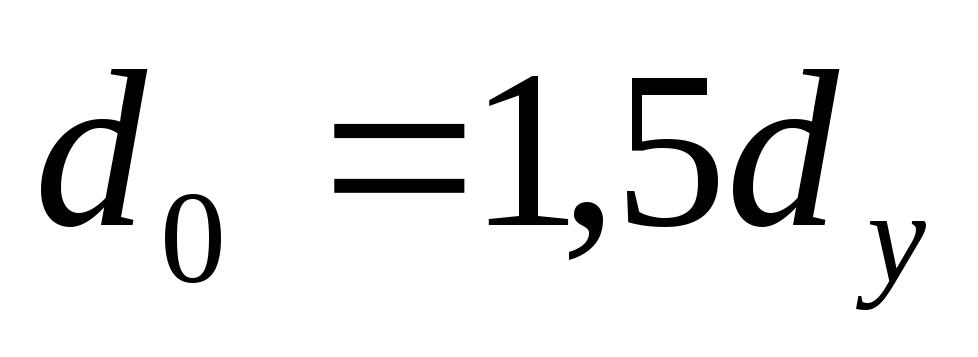 .
.
По условиям
выполнения кладки
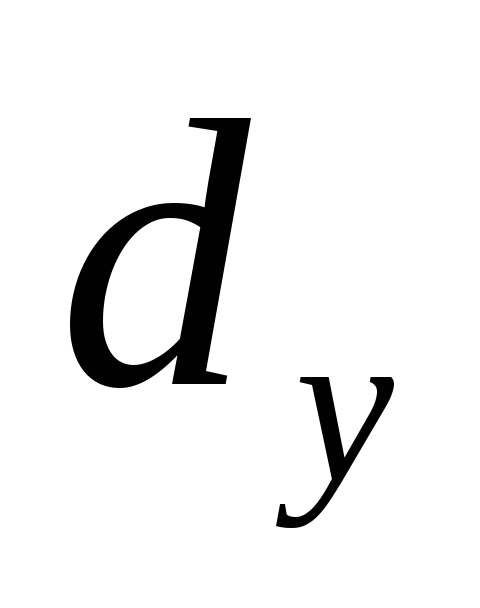 для кирпичных труб не должен быть меньше
0,8 м.
для кирпичных труб не должен быть меньше
0,8 м.
Падение температуры
газов на 1 м высоты трубы принимается
для кирпичных и железобетонных 1,0 –
1,5ºС, а для металлических 3 – 4 ºС.
Ориентировочно высота трубы может быть
определена по уравнению (26) без трёх
последних его членов. Подсчитав сумму
потерь всех видов на пути движения
газов от печи до основания дымовой
трубы, по уравнению (26) находят расчетную
высоту трубы
 .
Независимо от расчета высота дымовой
трубы по санитарным нормам должна быть
не менее 16 м и в 2 раза выше самого высокого
здания, находящегося в радиусе 100 м
вокруг трубы.
.
Независимо от расчета высота дымовой
трубы по санитарным нормам должна быть
не менее 16 м и в 2 раза выше самого высокого
здания, находящегося в радиусе 100 м
вокруг трубы.
Основной отличительной особенностью движения газа по трубам от движения капельных жидкостей заключается в том, что капельные жидкости характеризуются весьма малой сжимаемостью, а их вязкость практически не зависит от давления. По этой причине для решения большинства практических задач капельные жидкости можно считать не сжимаемыми, что позволяет значительно упростить уравнения движения такой жидкости. При движении газа таких допущений делать нельзя. Поскольку изучение общих решений уравнений газодинамики не является предметом настоящего курса, рассмотрим лишь частные задачи, встречающиеся в практике работы специалистов горных отраслей промышленности. К числу таких первоочередных задач относится изучение движения газов, включая воздух по газопроводам (воздуховодам).
Газ двигается по газопроводу при переменном давлении, т.к. давление изменяется вдоль длины газопровода из-за неизбежных потерь напора по длине трубопровода. По этой причине плотность газа и его вязкость являются величинами переменными и неодинаковы в различных сечениях газопровода. Рассмотрим наиболее простой случай газопровода (воздуховода) собранного из труб одинакового диаметра (простой газопровод S = const ) при установившемся движении газа. Тогда в соответствии с уравнением неразрывности потока газа массовый расход газа вдоль газопровода является величиной постоянной= const. При этом объёмный расход газа будет меняться от одного сечения газопровода к другому, т.к. плотность газа зависит от давления, которое по длине газопровода меняется.
![]()
Тогда скорость движения газа также будет меняться вдоль длины газопровода:
При этом должна изменяться и температура газа по длине газопровода, и, как следствие, также и вязкость газа. Однако для решения практических задач движение газа по трубопроводу можно считать изотермическим (небольшие скорости движения, теплоизоляция газопровода, небольшие перепады давления). Это допущение не приведет к серьёзным погрешностям в расчётах, но оно позволяет пренебречь изменением вязкости газа при незначительных колебаниях температуры газа в газопроводе. Т.е. полагаем, что в газопроводе соблюдается условие: Т = const и= const. При таких условиях будет постоянным для всего потока и число Рейнольдса, и как следствие будут одинаковым коэффициенты трения и гидравлических сопротивлений по длине потока.
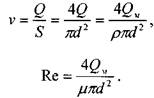
Отметим, что в последнем выражении все величины, входящие в правую часть равенства являются величинами постоянными, отсюда: Re = const и /I = const. По этой причине для определения величины потерь напора и расхода газа можно воспользоваться обычным уравнением Бернулли.
| Предыдущие материалы: |