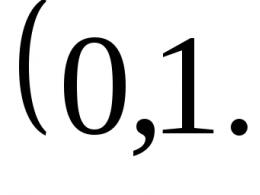Напряжение внутри жидкости, находящейся в состоянии покоя, называется гидростатическим давлением.

Средним гидростатическим давлением называется среднее для данной площадки напряжение сжатия, вызванное силой . Это давление можно определить как отношение к , то есть

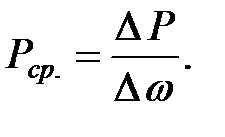(1.8)

Гидростатическое давление в данной точке определяется, как предел отношения к при 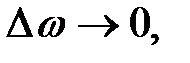то есть

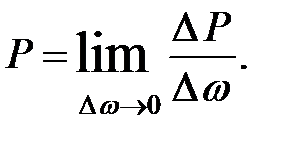(1.9)

Абсолютное гидростатическое давление в любой точке жидкости складывается из давления на её свободную поверхность и давления столба жидкости, высота которого равна расстоянию от этой точки до свободной поверхности (рис. 1.1).

Основное уравнение гидростатики будет иметь вид

где – полное или абсолютное гидростатическое давление в данной точке М ;

– давление на свободной поверхности;

z – координата точки М ;

z 0 – координата свободной поверхности;

OX – плоскость сравнения;

r – плотность жидкости;

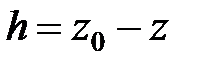– высота слоя жидкости над точкой М .

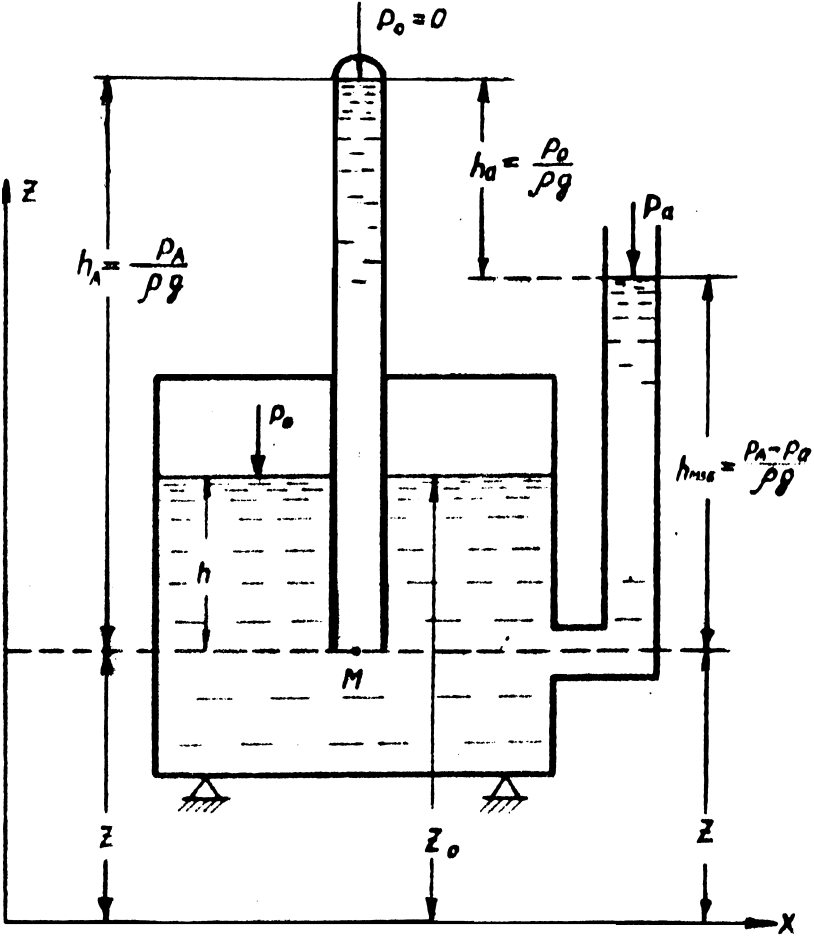
Если сосуд открыт, то давление на свободной поверхности равняется атмосферному давлению

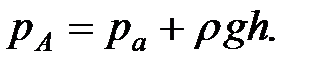(1.11)

Величина превышения абсолютного давления в точке над атмосферным давлением называют избыточным или манометрическим давлением

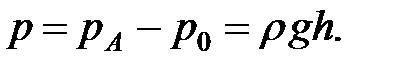(1.12)

Если в какой-либо точке абсолютное давление меньше атмосферного, то состояние жидкости характеризуется так называемым вакуумом. Разность между атмосферным и абсолютным давлением называется вакуумметрическим давлением

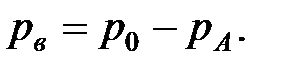(1.13)

На основании основного уравнения гидростатики может быть сформулирован закон Паскаля : внешнее давление, приложенное к свободной поверхности жидкости в замкнутом сосуде, передаётся в любую точку жидкости без изменения.

На способности жидкости передавать изменение внешнего давления во все точки занятого ею пространства основан принцип действия гидравлических машин. На рис. 1.2 показана схема действия гидравлического пресса.

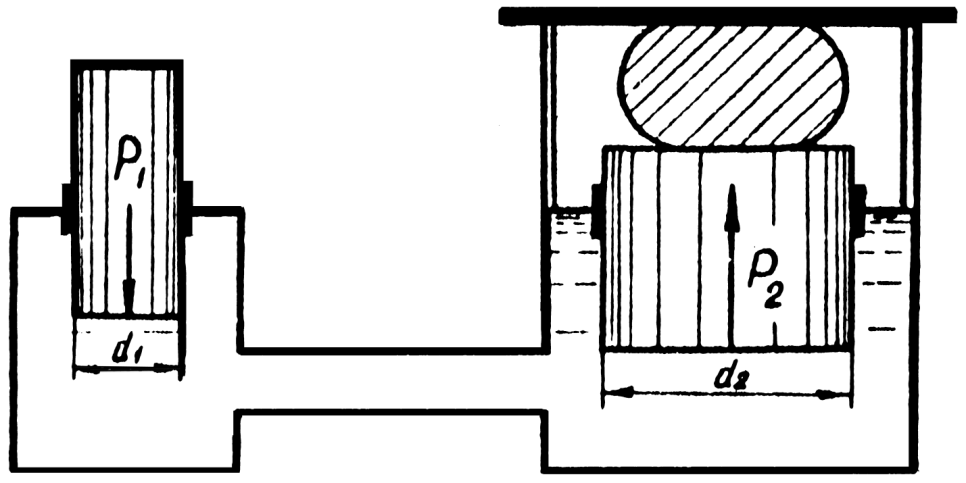
Если на малый поршень действует сила P 1 , то сила, действующая на большой поршень P 2 , определяется по уравнению:

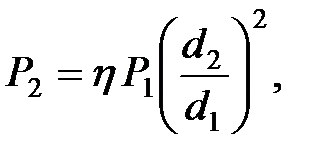(1.14)

где = 0,8-0,85 – коэффициент полезного действия гидравлического пресса, учитывающий потери на трение.

Гидростатическое давление измеряют в паскалях. Паскаль (Па ) – давление, вызываемое силой 1 ньютон (Н ), равномерно распределённой по нормальной к ней поверхности площадью 1 м 2 .

При решении практических задач, где возникает необходимость перевода ранее применявшихся единиц измерения давления в СИ, будем пользоваться соотношениями:

1 ат = 1 кг/см 2 = 10 м вод. cт. = 98065 Па » 98,1 кПа

760 мм рт. cт. = 101325 Па » 101,3 кПа .

Задачи

1.18. Какая высота водяного столба соответствует давлению 150 кПа ?

Решение . Из формулы (1.12) следует, что

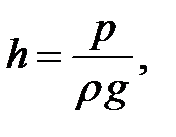
где p = 1,5×10 5 Па – избыточное давление, создаваемое столбом воды;

r = 1×10 3 кг /м 3 – плотность воды.

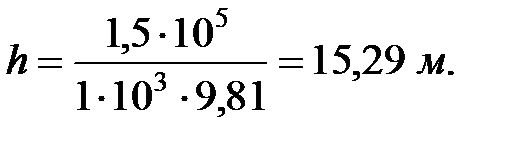
1.19. Какая высота ртутного столба соответствует давлению 80 кПа ?

1.20. Определить величину избыточного давления на поверхности жидкости, находящейся в закрытой ёмкости (рис. 1.3) в состоянии покоя, если в трубке пьезометра вода поднялась на высоту h = 1,8 м .

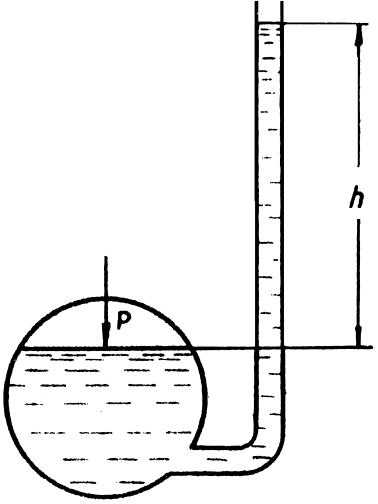
1.21. На какой высоте над манометром, присоединённым к резервуару, находится уровень нефти плотностью 840 кг /м 3 . Манометр показывает давление 1,21×10 5 Па .

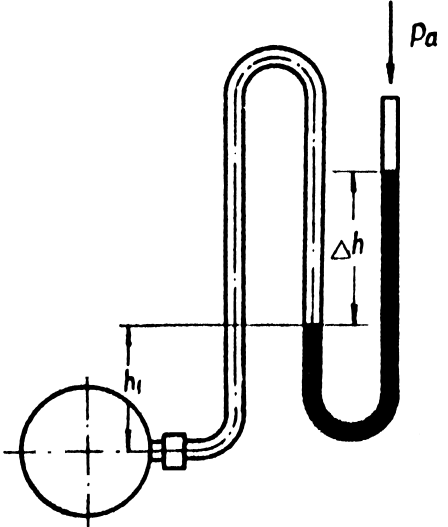
1.22. Определить избыточное давление воды в трубопроводе, если
U -образный ртутный манометр (рис. 1.4) показал перепад Dh = 80 см ,
а h 1 = 40 см .

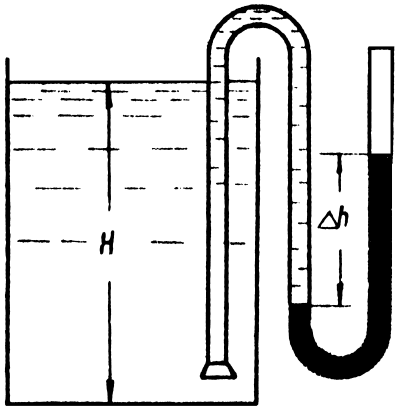
1.23. Определить уровень мазута в баке (рис. 1.5), если при замере
S -образной трубкой, разность уровней ртути Dh = 250 мм . Плотность мазута r = 860 кг /м 3 .

1.24. Манометр, с помощью которого производилось измерение давления в наружной водопроводной сети, показал 2 кг/см 2 . Определить абсолютное давление в сети, если атмосферное давление 750 мм рт. cт.

Решение . Абсолютное давление в наружной водопроводной сети определяется по формуле (1.11), где – атмосферное давление

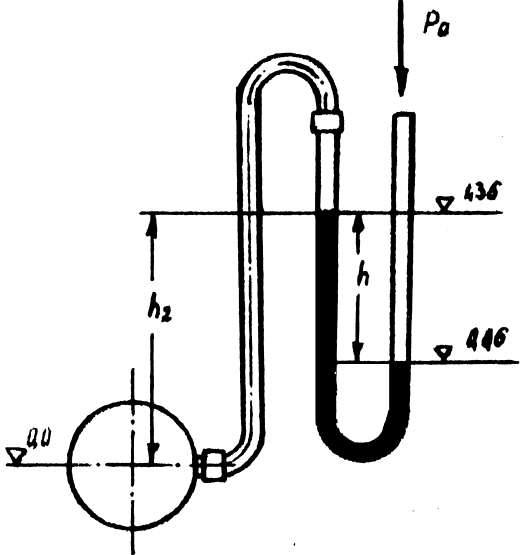
1.25. Определить абсолютное и вакуумметрическое давление воды
в трубопроводе, если U -образный ртутный манометр (рис. 1.6) показал перепад Dh = 50 см . Атмосферное давление 760 мм рт. ст. Высотные отметки относительно оси трубопровода показаны на рис. 1.6.

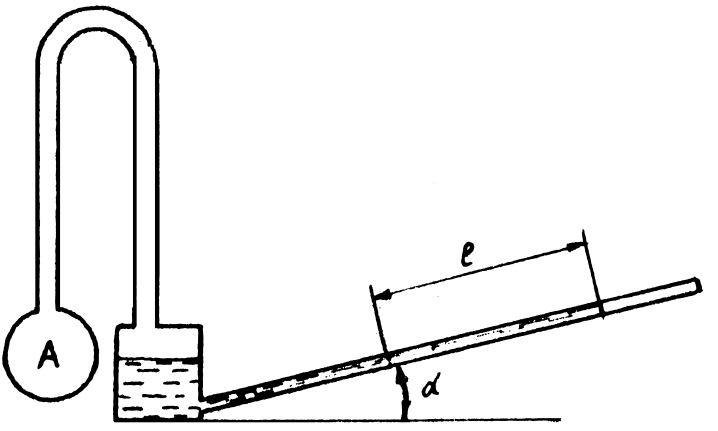
1.26. Давление в газопроводе А измеряется с помощью микроманометра, заполненного спиртом плотностью r = 790 кг /м 3 . Трубка микроманометра наклонена к горизонту под углом a = 15° (рис. 1.7). Определить избыточное давление в газопроводе, если мениск переместился на l = 62 мм.

1.27. Определить абсолютное и избыточное давление на дно пожарного водоёма глубиной 3,5 м . Атмосферное давление 735 мм рт. ст.

1.28. Определить абсолютное и избыточное давление на дно водонапорного бака диаметром 3 м , в котором находится 15 м 3 воды. Атмосферное давление 750 мм рт. ст.

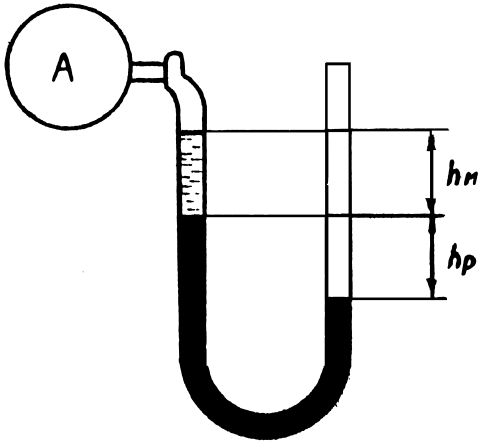
1.29. Определить абсолютное и избыточное давление в резервуаре по показанию ртутного дифференциального манометра (рис. 1.8), в правом колене которого над ртутью находится столб масла высотой 15 см плотностью 850 кг /м 3 . Высота столба ртути 40 см , атмосферное давление 730 мм рт. ст.

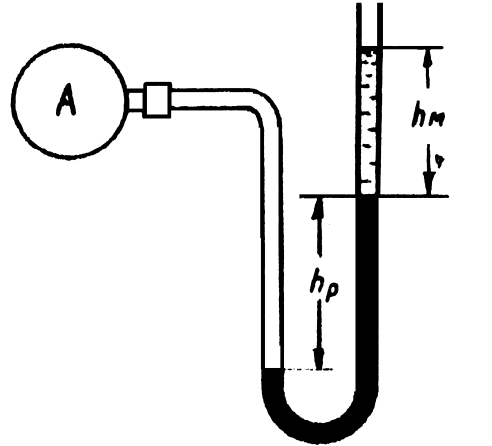
1.30. Определить абсолютное и вакуумметрическое давление во всасывающей линии ацетиленового компрессора по показанию ртутного вакуумметра (рис. 1.9). Ртуть в левом колене поднялась на высоту h p = 50 см , над ртутью налито масло h м = 20 см плотностью 800 кг /м 3 . Атмосферное давление 750 мм рт. ст.

1.31. Определить избыточное давление в сети наружного пожарного водопровода, питающегося от водонапорной башни высотой 25 м .

1.32. Определить максимальную высоту слоя нефти плотностью 900 кг /м 3 , чтобы избыточное давление на дно резервуара не превышало 70 кПа .

1.33. Определить на какую высоту может подняться вода из водяного бака гидропневматической установки, если манометр, установленный на воздушном баке, показывает 3,2 кг/см 2 .

1.34. Определить максимальную глубину воды в водонапорном баке объемом 30 м 3 , установленном на перекрытии. Дополнительная нагрузка на перекрытии от установки бака с водой не должна превышать 2×10 4 Па . Вес бака с арматурой 8 т.

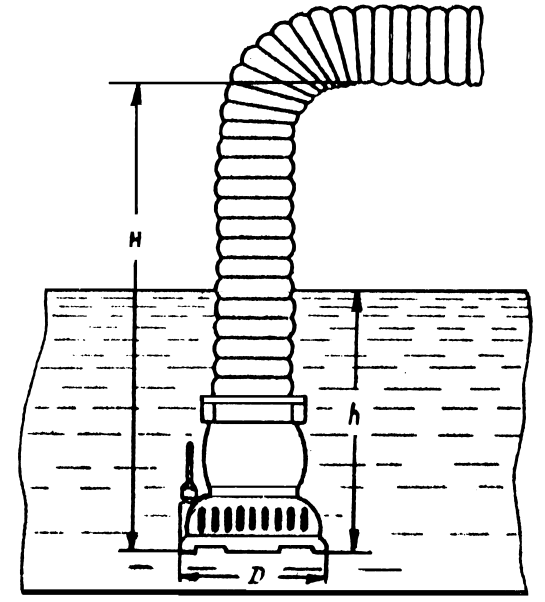
1.35. Определить усилие, необходимое для открытия всасывающего клапана пожарного насоса диаметром 200 мм , если длина рукава H = 6 м ,
а глубина погружения всасывающего клапана h = 1 м (рис. 1.10)

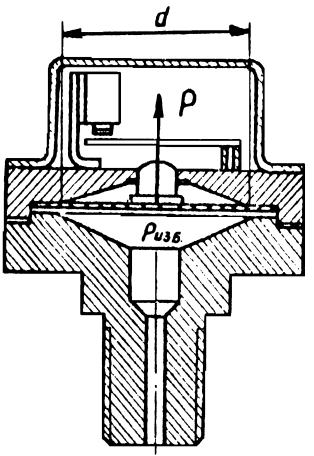
1.36. Определить силу, действующую на шток сигнализатора давления, если давление на мембрану диаметром 40 мм составляет 3,5×10 5 Па (рис. 1.11).

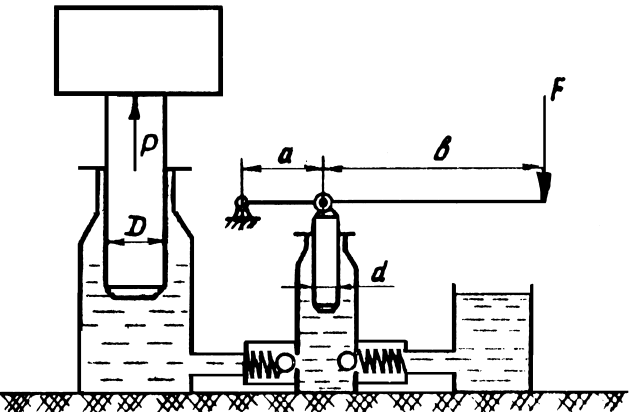
1.37. Для подъёма пожарной техники во время ремонта применяется гидродомкрат (рис. 1.12). Определить силу, развиваемую гидродомкратом, если сила F , действующая на рукоятку, составляет 20 Н , а /в = 1/9, d 2 /d 1 = 10. Коэффициент полезного действия h = 0,85.

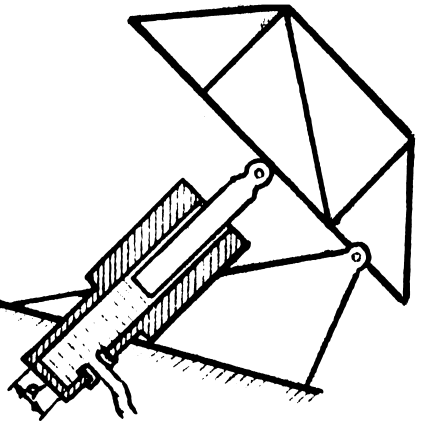
1.38. Определить давление масла в цилиндре гидропривода пожарной лестницы (рис. 1.13), если диаметр поршня 100 мм . Усилие на штоке поршня 30 кН , коэффициент полезного действия h = 0,95.

1.3. Эпюры гидростатического давления.
Сила гидростатического давления на плоские стенки.
Закон Архимеда

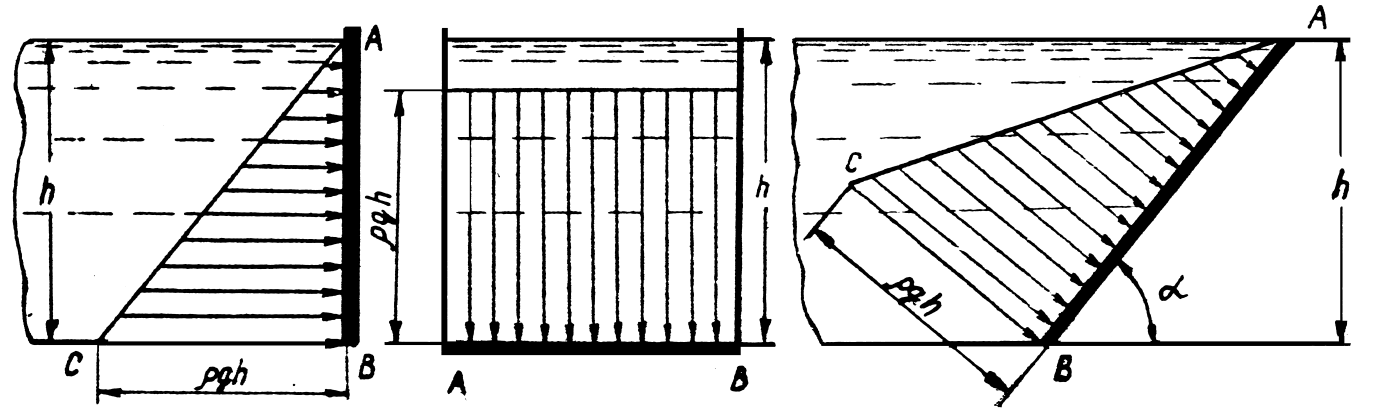
Графическое изображение распределения гидростатического давления по поверхности тела, погруженного в жидкость, называется эпюрой гидростатического давления .

При построении эпюр гидростатического давления используются два основных принципа, вытекающие из свойств гидростатического давления:

· гидростатическое давление является векторной величиной . Вектор гидростатического давления направлен по нормали к поверхности тела, погруженного в жидкость;

· модуль вектора гидростатического давления определяется по уравнению (1.11) для построения эпюр абсолютного давления и (1.12) для построения эпюр избыточного гидростатического давления.

Для плоских прямоугольных стенок эпюры избыточного и абсолютного гидростатического давления имеют вид, представленный на рис. 1.14
и рис. 1.15.

Равнодействующая элементарных сил гидростатического давления, действующих на какую-либо стенку, называется силой гидростатического давления .

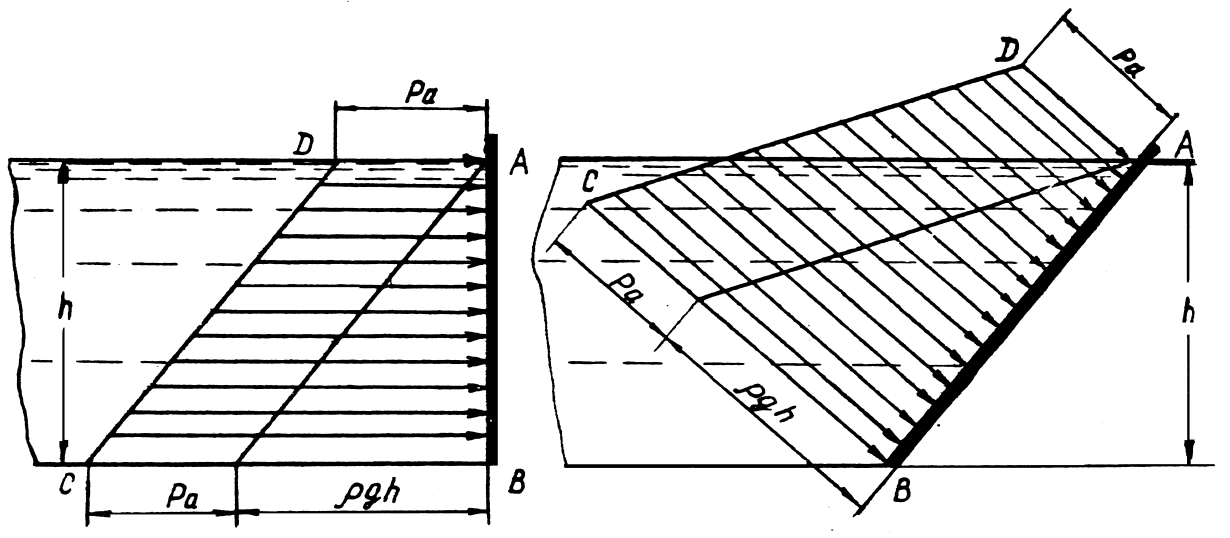
Сила гидростатического давления на площадку определяется произведением её площади на гидростатическое давление в центре тяжести площадки (рис. 1.16).

где P – сила гидростатического давления, Н ;

h цт – глубина погружения центра тяжести фигуры, м;

p цт – гидростатическое давление в центре тяжести фигуры, Па .

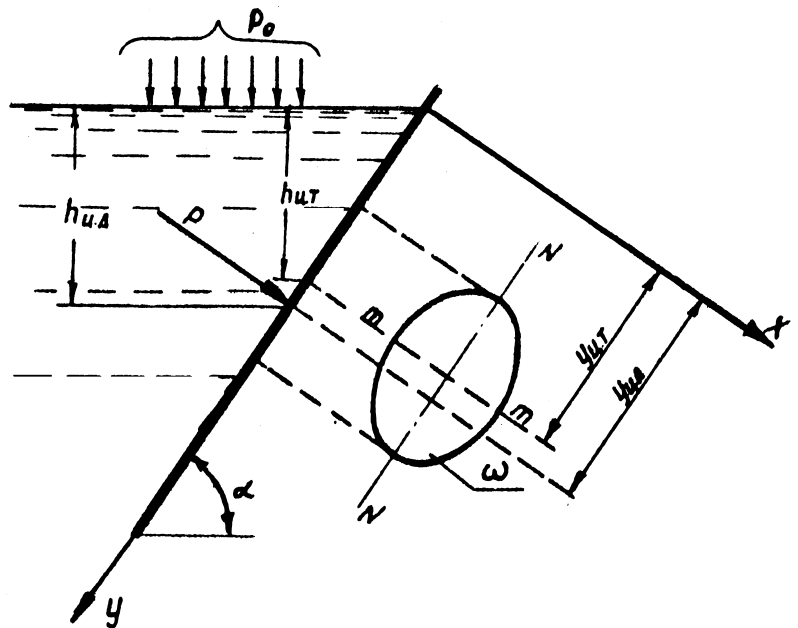
Точка приложения силы Р называется центром давления. Координата центра давления для симметричных относительно оси N-N фигур определится из уравнения

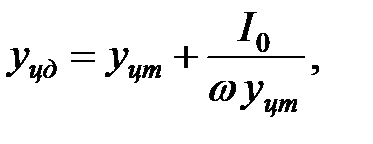(1.16)

где I 0 – момент инерции площади w относительно оси m-m .

Значения I 0 и y цт для некоторых фигур приведены в приложении 5.

Сила гидростатического давления Р может быть определена графическим способом как произведение площади эпюры гидростатического давления на ширину стенки.

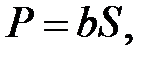(1.17)

где S – площадь эпюры гидростатического давления, Н /м ;

b – ширина стенки, м .

Сила давления проходит через центр тяжести эпюры гидростатического давления и направлена по нормали к поверхности.

Сила избыточного гидростатического давления для плоских прямоугольных стенок, изображенных на рис. 1.14, может быть определена по формулам:

Вертикальная стенка

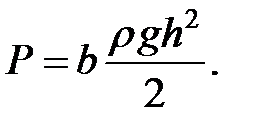(1.18)

Горизонтальная стенка

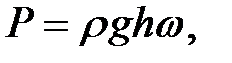(1.19)

где w – площадь дна, м 2 .

Наклонная стенка

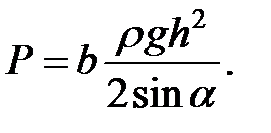(1.20)

Жидкости и газы передают по всем направлениям приложенное к ним давление. Об этом гласит закон Паскаля и практический опыт.

Но существует еще и собственный вес, который тоже должен влиять на давление, существующее в жидкостях и газах. Вес собственных частей или слоев. Верхние слои жидкости давят на средние, средние на нижние, а последние - на дно. То есть мы можем говорить о существовании давления столба покоящейся жидкости на дно.

Формула давления столба жидкости

Формула для расчета давления столба жидкости высотой h имеет следующий вид:

где ρ - плотность жидкости,
g - ускорение свободного падения,
h - высота столба жидкости.

Это формула так называемого гидростатического давления жидкости.

Давление столба жидкости и газа

Гидростатическое давление, то есть, давление, оказываемое покоящейся жидкостью, на любой глубине не зависит от формы сосуда, в котором находится жидкость. Одно и то же количество воды, находясь в разных сосудах, будет оказывать разное давление на дно. Благодаря этому можно создать огромное давление даже небольшим количеством воды.

Это очень убедительно продемонстрировал Паскаль в семнадцатом веке. В закрытую бочку, полную воды, он вставил очень длинную узкую трубку. Поднявшись на второй этаж, он вылил в эту трубку всего лишь одну кружку воды. Бочка лопнула. Вода в трубке из-за малой толщины поднялась до очень большой высоты, и давление выросло до таких значений, что бочка не выдержала. То же самое справедливо и для газов. Однако, масса газов обычно намного меньше массы жидкостей, поэтому давление в газах, обусловленное собственным весом можно часто не учитывать на практике. Но в ряде случаев приходится считаться с этим. Например, атмосферное давление, которое давит на все находящиеся на Земле предметы, имеет большое значение в некоторых производственных процессах.

Благодаря гидростатическому давлению воды могут плавать и не тонуть корабли, которые весят зачастую не сотни, а тысячи килограмм, так как вода давит на них, как бы выталкивая наружу. Но именно по причине того же гидростатического давления на большой глубине у нас закладывает уши, а на очень большую глубину нельзя спуститься без специальных приспособлений - водолазного костюма или батискафа. Лишь немногие морские и океанические обитатели приспособились жить в условиях сильного давления на большой глубине, но по той же причине они не могут существовать в верхних слоях воды и могут погибнуть, если попадут на небольшую глубину.

Гидростатическое давление - давление столба воды над условным уровнем.

Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине этой поверхности, и направленной по нормали к ней. Отношение Pw, то есть давление р на поверхность равную единице, называется гидростатическим давлением.

Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах.

Вычисление

В каждой жидкости существует давление, обусловленное её собственным весом p = G / S = m g / S {\displaystyle p=G/S=mg/S} ; так как m = ρ V {\displaystyle m=\rho V} , то p = ρ g V / S {\displaystyle p=\rho gV/S} , учтем что V = S h {\displaystyle V=Sh} и получим формулу p = ρ g h {\displaystyle p=\rho gh}

Плотность жидкости ρ зависит от температуры. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением .

История открытия

Единица измерения

В практике Гидростатическое давление измеряют в кг на 1 кв. см. Большие давления выражают часто в атмосферах, принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0° под широтой, где ускорение силы тяжести = 0,0635 кг на 1 см² = 6,21·10 6 дин на 1 кв. см. 1 атмосфера = 1,0333 кг на 1 см² = 1,0136·10 6 дин на 1 см² для широты Парижа или 1,0132·10 6 для широты в 45°.

На основании гидростатического парадокса можно Г. давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности: так давление в 1 фн. на кв. дм. равно давлению столба воды в 25 дм высотой, так как фн. есть вес 25 куб. дм. воды.

Гидростатический парадокс

Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние каждой такой частицы от свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу Г. давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.

Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, Г. давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.

Закон Паскаля

Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести (= несжимаемая жидкость ) подчиняется закону Паскаля :

В.И.КРЮКОВА ,
МОУ СОШ № 7, г. Прокопьевск, Кемеровская обл.

Гидростатическое давление

Урок объяснения нового матерала. 7-й класс

Цель урока : рассмотреть природу давления столба жидкости; выработать практические навыки при решении задач; развивать познавательную активность учащихся.

Ход урока

I. Проверка домашнего задания

Фронтальная беседа. Сформулируйте закон Паскаля. Чем отличается передача давления жидкостями и газами от передачи давления твёрдыми телами? Отвечайте, используя сведения о молекулах. Забавляясь, мы любим выдувать мыльные пузыри (демонстрация ). Почему они имеют форму шара? Почему взрыв снаряда губителен для находящихся поблизости организмов? Каким простым способом можно удалить вмятину на оболочке теннисного мяча? (Мяч пластмассовый.) Почему пустой бумажный мешок, надутый воздухом, с треском разрывается, если ударить по нему рукой или обо что-либо твёрдое?

II. Объяснение нового материала

Проблемная ситуация . Как раньше добывался жемчуг? Почему ныряльщики часто погибали? Что вы испытываете при нырянии в воду? Зачем нужен жёсткий скафандр для водолазов, работающих на глубине? Камбала обитает на морском дне. Почему её тело плоское?

Опыт 1 . В трубку, дно которой затянуто плёнкой, наливаем воду. Дно прогибается. Почему?

Давление, производимое покоящейся жидкостью, называется гидростатическим давлением .

Выделяем столб жидкости высотой h и площадью основания S ;

сила давления воды на основание:

F = p S . (1)

F = P – весу жидкости,

F = P = mg , m = V ,

V = S h .

F = Shg . (2)

Приравниваем формулы (1) и (2):

Анализ формулы . Давление жидкости зависит:

1) от жидкости (чем больше плотность жидкости, тем больше давление);

2) от h (чем больше высота столба жидкости, тем больше давление).

А зависит ли давление жидкости от площади дна сосуда? Согласно формуле, не зависит.

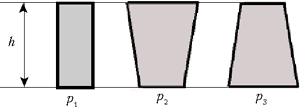
Вывод : давление жидкости не зависит от площади дна сосуда и его формы.

При одинаковой высоте h давление одинаково: р 1 = р 2 = р 3 . А теперь докажем, что внутри жидкости существует давление.

Опыт 2 . Пластинка (крышка от банки из-под кофе) закрывает снизу полый стеклянный цилиндр, опущенный в сосуд с жидкостью, и удерживается под ним.

Проблемная ситуация . Если жидкости нет, пластинка падает. Почему? (Учащиеся отвечают, что это происходит под действием силы тяжести .)

Если в сосуд налита жидкость, пластинка удерживается под цилиндром до тех пор, пока внутри цилиндра жидкости нет, и падает, когда уровни жидкости внутри и снаружи цилиндра совпадают. (Учащиеся свободно отвечают, что в последнем случае давление жидкости над пластинкой равно давлению под пластинкой .)

(Можно пронаблюдать давление внутри жидкости, используя манометр, соединённый с коробочкой, затянутой резиновой мембраной.)

Опыт 3 . В полиэтиленовый пакет наливаем подкрашенную воду, погружаем его в аквариум (банку), чтобы уровни жидкостей совпадали. Если нажать на стенку пакета в каком-либо месте, то вмятина сохраняется. Почему? Если пакет погружать глубже, то подкрашенная жидкость (вода) в пакете поднимается вверх. Почему?

Аккуратно делаем надрез ножницами (отрезаем угол пакета) – жидкости не перетекают. Поднимаем пакет вверх – жидкость из пакета начинает перетекать в аквариум. Почему?

Вывод : внутри жидкости существует давление, которое на одном уровне одинаково во всех точках и увеличивается с глубиной погружения.

Отвечаем на проблемные вопросы, прозвучавшие в начале урока.

А можно ли при помощи небольшого количества воды создать большое давление? По рисунку учебника рассматриваем опыт Паскаля.

III. Решение задач

Вызываю к доске троих учащихся и предлагаю решить задачи:

В сосуды одинаковой формы и объёма до одной высоты 40 см налиты жидкости: в первый – керосин, во второй – вода, в третий – ртуть. Рассчитайте давление в каждом случае.

После решения учащиеся наглядно оценивают, сравнивая результаты, что, чем больше плотность жидкости, тем большее давление она оказывает.

Дополнительно, если позволяет время, решаем задачу:

Определите давление и силу давления керосина на дно бака площадью 4,5 дм 2 , наполненного до высоты 25 см. (Ответ . 1960 Па; 88,2 Н.)

IV. Домашнее задание

С.В.Громов , Н.А.Родина . Физика-7 § 37, вопрос № 87.